Тема 1.2. Корни, степени и логарифмы

Мы уже знакомы с множествами натуральных, целых и рациональных чисел и знаем, что в этих множествах можно производить такие операции как сложение, вычитание, умножение и деление.

Рассмотрим теперь операции возведение в степень и извлечение корня.

Возведение в степень. Мы знаем, что степень числа есть произведение равных сомножителей. Так, например, произведение 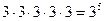. В общем случае, если , то число а называется основанием степени, n – показателем степени, число b – степенью.

По определению степени, как произведение равных сомножителей, символ имеет смысл лишь при натуральном n, так как перемножить можно лишь натуральное число сомножителей. Что же касается таких символов как, например, и т.п., то они не подходят к приведенному выше определению степени. Поэтому, чтобы обобщить понятие степени и распространить его на целые, рациональные и действительные показатели, нужно символу , придать смысл с помощью другого определения.

Известно, что для натуральных показателей m и n степень любого числа a обладает следующими основными свойствами:

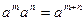(1)

(2)

Поэтому, при обобщении степени на целые и рациональные показатели, свойства (1) и (2) должны сохраняться.

Нулевой показатель.

Если 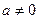, то условимся считать .

Для такого определения нулевого показателя свойства (1) и (2) сохраняются.

Например, .

Отрицательный показатель.

Если 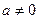, то условимся считать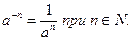

При таком определении степени с отрицательным показателем свойства (1) и (2) также сохраняются. Например, .

Дробный показатель.

Прежде чем перейти к степени с дробным показателем, вспомним определение корня степени n из числа a.

Корнем n-й степени из числа а называется число b такое, что .

Число а называется подкоренным выражением, n – показателем корня. Обозначение: .

Мы будем рассматривать случай, когда показатель корня есть натуральное число. Из школьного курса математики нам известно, что при четных показателях корень из отрицательного числа не имеет смысла, так как действительное число в четной степени не может быть равно отрицательному числу. В остальных случаях корень из любого числа имеет смысл. Например, . Корень из любого положительного числа в четной степени имеет два значения, отличающееся знаками. Так, например, 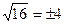. Положительное значение корня с четным показателем называется арифметическим корнем.

Теперь перейдем к степени с дробным показателем.

Если , то условимся считать .

Дробной степенью числа называется величина .

Свойства дробных степений:

1. Если показатель корня и показатель степени в подкоренном выражении имеют общий делитель, то показатель корня и показатель степени в подкоренном выражении можно сократить на этот делитель: .
2. Если показатель корня и показатель степени в подкоренном выражении умножить на одно и то же натуральное число, то новое выражение равно исходному: .
3. Чтобы корень n-й степени возвести в некоторую степень m нужно подкоренное выражение возвести в степень m: .

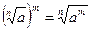Пример. Упростить выражение .

Решение. Упростим делимое: .

Упростим теперь делитель: .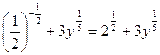

Так как делитель равен первому сомножителю делимого, то при делении эти выражения сократятся, поэтому в результате деления получим ответ: .

Перечислим свойства операции возведения в степень для любых числовых множеств, выражающиеся равенствами и неравенствами.

Свойства, выражающиеся равенствами:

1.

2.

3.

4.

5.

6.

7.

Свойства, выражающиеся неравенствами:

1. если , то
2. если
3. если
4. если при четном n и при нечетном n.

Логарифмом числа N по основанию a (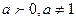) называется показатель степени, в которую надо возвести число a, чтобы получить число N: если 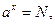то

Например, так как ;

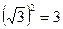так как ;

так как

Из определения логарифма следует основное логарифмическое тождество: Согласно этому тождеству:

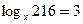Пример. Найдите х, если: а) ; б) ; в)

Пример. Вычислите: а) 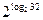; б) ; в)

 

Сформулируем основные свойства логарифмов.

Теорема 1. Логарифм произведения двух положительных чисел по основанию а (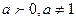) равен сумме логарифмов множителей по тому же основанию:

где

Пример. Дано: 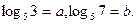Вычислите: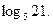

Решение.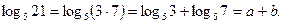

 

Теорема 2. Логарифм частного двух положительных чисел по основанию a (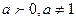) равен разности логарифмов числителя и знаменателя по тому же основанию:

где

Пример. Дано: 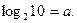Найдите

Решение.

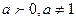Теорема 3. Логарифм степени по основанию a () равен произведению показателя m на логарифм числа х по основанию а:

где

 

Пример. Найдите

Решение.

Теоремы 1-3 свидетельствуют о том, что действия умножения, деления, возведения в степень могут быть сведены к более простым действиям – соответственно сложению, вычитанию логарифмов, умножению логарифма на некоторое число.

 

Теорема 4. Логарифм положительного числа по данному основанию равен частному от деления логарифма этого же числа по новому основанию на логарифм данного основания по новому основанию:

где

Это соотношение называют формулой перехода от логарифма по основанию а к логарифму по основанию b.

 

Пример. Вычислите

Решение. Заметим, что числа 16 и 64 являются степенями числа 4. Получим:

С помощью формул перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов. Десятичными называют логарифмы по основанию 10 и обозначают 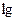, а с натуральными мы познакомимся позже.

Отметим еще некоторые свойства логарифмов: 1)

2) При любом

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: