 |
Задания для контрольной работы
|
|
|
|
Номер варианта контрольной работы определяется по таблице в зависимости от первой буквы фамилии.
| Первая буква фамилии | Номер варианта контрольной работы | Первая буква фамилии | Номер варианта контрольной работы | |
| А, Л, Х | Е, Р, Э | |||
| Б, М, Ц | Ж, С, Ю | |||
| В, Н, Ч | З, Т, Я | |||
| Г, О, Ш | И, У | |||
| Д, П, Щ | К, Ф |
Задание 1. Представить обыкновенную дробь в виде периодической десятичной дроби
| № варианта | а) | б) | № варианта | а) | б) | |
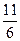
| 
| 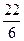
| 
| |||
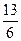
| 
| 
| 
| |||
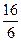
| 
| 
| 
| |||

| 
| 
| 
| |||
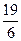
| 
| 
| 
|
Задание 2. Обратить десятичные периодические дроби в обыкновенные дроби
| № варианта | а) | б) | № варианта | а) | б) | |
| 2,(3) | 0,1(12) | 1,(7) | 0,2(17) | |||
| 3,(4) | 0,2(13) | 3,(6) | 0,3(12) | |||
| 1,(5) | 0,3(15) | 1,(3) | 0,4(13) | |||
| 2,(6) | 0,4(17) | 2,(5) | 0,7(21) | |||
| 3,(7) | 0,1(15) | 1,(4) | 0,2(16) |
Задание 3. Выполнить действия. Результат представить в виде обыкновенной дроби
| № варианта | № варианта | |||
| 1,2 + 2,(3) | 1,4 + 2,(6) | |||
| 2,3 + 3,(2) | 1,5 + 1,(4) | |||
| 0,6 + 1,(3) | 1,9 + 0,2(3) | |||
| 0,8 + 2,(7) | 1,7 + 2,(1) | |||
| 1,2 + 0,1(3) | 1,8 + 1,(7) |
Задание 4. Вычислить
| № варианта | |
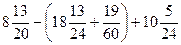
| |

| |

| |
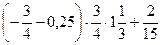
| |

| |

| |

| |
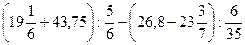
| |
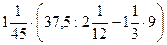
| |

|
Задание 5. Найти абсолютную и относительную погрешность измерений.
Вариант 1-5.
Истинный вес детали х кг. При взвешивании вес оказался равным а кг. Найти абсолютную и относительную погрешность при взвешивании.
| Вариант | х | а |
| 132,4 | 132,5 | |
| 128,9 | 128,5 | |
| 25,7 | 26,0 | |
| 24,5 | 24,1 | |
| 74,9 | 74,2 |
Вариант 6-10.
Точное число жителей поселка х человек. Данные статистики округленно показывают а человек. С какой абсолютной и относительной погрешностью произведен расчет?
|
|
|
| Вариант | х | а |
| 25 623 | 25 600 | |
| 17 826 | 17 800 | |
| 16 125 | 16 000 | |
| 27 826 | 27 800 | |
| 13 562 | 13 500 |
Задание 6. Выполнить действия с приближенными числами
| Вариант | а) | б) | в) |
| 32,5676 + 15,835 + 5,2 | 20,361 + 50,26 + 6,356 | 81,52 + 56,02 + 89,239 | |
| 5,781 + 56,782 - 5,3 | 56,032 + 0,7890 – 56,2 | 16,2689 + 18,536 + 6,3 | |
| 20,569 + 52,78 – 0,5 | 26,5 + 89,5623 + 0,71 | 52,638 + 81,012 + 52,4 | |
| 52,638 + 16,23 + 79,3 | 52,96 + 78,2 + 93,45 | 56,2 + 45,7 – 0,591 | |
| 45,12 + 89,41 – 0,8 | 26,53 + 0,89 + 12,3 | 42,89 + 40,125 – 5,032 | |
| 45,89 + 56,0125 – 5,3 | 45,29 + 4,128 – 2,9 | 23,897 + 52,4 + 41,12 | |
| 42,89 + 8,123 – 2,5 | 45,8 + 50,124 – 8,935 | 58,931 + 5,1238 + 0,26 | |
| 82,56 + 89,2 + 12,323 | 45,2387 + 5,321 – 2,1 | 45,78 + 0,128 + 0,42 | |
| 12,069 + 2,371 – 0,26 | 45,2378 + 16,459 + 2,3 | 12,5 + 50,298 – 0,21 | |
| 0,1289 + 23,41 – 1,9 | 45,891 + 4,8597 + 0,23 | 25,8926 + 5,3 + 19,526 |
Задание 7. Вычислить
| Вариант | а) | б) | Вариант | а) | б) |

| 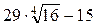
| 
| 
| ||
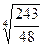
| 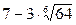
| 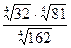
| 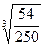
| ||

| 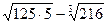
| 
| 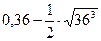
| ||
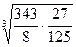
| 
| 
| 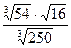
| ||

| 
| 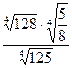
| 
|
Задание 8. Представить выражение в виде степени с рациональным показателем
| Вариант | а) | б) | Вариант | а) | б) |
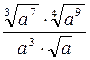
| 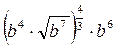
| 
| 
| ||
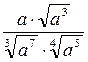
| 
| 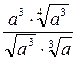
| 
| ||
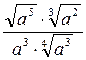
| 
| 
| 
| ||
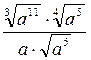
| 
| 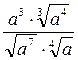
| 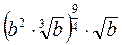
| ||

| 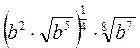
| 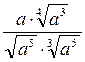
| 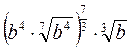
|
Задание 9. Упростить выражение и вычислить его значение
| Вариант | Вариант | ||

| 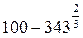
| ||
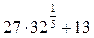
| 
| ||

| 
| ||
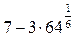
| 
| ||

| 
|
Задание 10. Решите уравнение
| Вариант | Вариант | ||

| 
| ||

| 
| ||

| 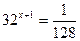
| ||

| 
| ||

| 
|
Задание 11. Решите уравнение
| Вариант | Вариант | ||

| 
| ||

| 
| ||

| 
| ||

| 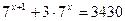
| ||
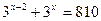
| 
|
Задание 12. Вычислить логарифмы
| Вариант | а) | б) | в) |
| log268 – log217 | log15 
| 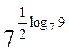
| |

| 
| log2log981 | |
| log210 – log25 + log28 | log3log28 | 
| |

| log2log416 | 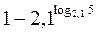
| |

| (log103000 – log103) 
| 
| |
| log268 – log217 | 
| 
| |
| log4192 – log43 | 
| 
| |

| 
| 
| |

| 
| 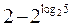
| |
| log4192 – log43 | 
| log2log381 |
Задание 13.
| Вариант | |
 Выразите через а: Выразите через а: 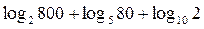
| |
 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
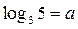 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
 Выразите через а: Выразите через а: 
| |
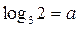 Выразите через а: Выразите через а: 
|
Задание 14. Решите уравнение
|
|
|
| Вариант | а) | б) |
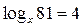
| 
| |

| 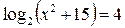
| |

| 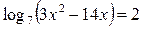
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 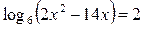
| |

| 
|
Задание 15. Представить в виде произведения выражение
| Вариант | Вариант | ||
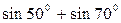
| 
| ||

| 
| ||
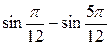
| 
| ||

| 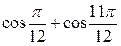
| ||
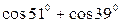
| 
|
Задание 16. Упростить выражение
| Вариант | |

| |
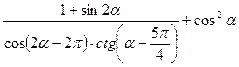
| |

| |

| |

| |

| |

| |

| |

| |

|
Задание 17. Решите уравнение
| Вариант | |
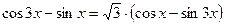
| |
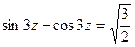
| |

| |
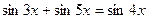
| |

| |
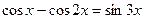
| |

| |

| |
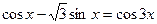
| |

|
Задание 18. Вычислить
| Вариант | |

| |
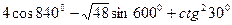
| |

| |

| |
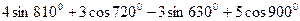
| |

| |
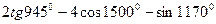
| |
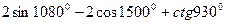
| |

| |
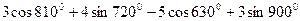
|
Справочные материалы
Корни и степени
Свойства корней



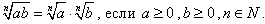

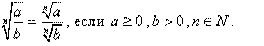



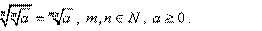

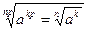

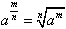 , где m? Z, n? N, n > 1, a > 0;a0 = 1, где a ≠ 0. , где m? Z, n? N, n > 1, a > 0;a0 = 1, где a ≠ 0.
|
Свойства степени с рациональным показателем
Если a > 0, b > 0, p, q? Q, то справедливы следующие свойства утверждения:

t и p – рациональные числа
Показательные неравенства
af(x) >ag(x),
где a – положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.
Показательное неравенство af(x) >ag(x) равносильно неравенству того же смысла
f(x) > g(x), если a > 1.
Показательное неравенство af(x)>ag(x) равносильно неравенству противоположного смысла f(x) < g(x ), если 0 < a < 1.
Логарифм числа


Свойства логарифмов
1. loga (c1c2)= loga c1 + loga c2
2. loga  = loga c1 - loga c2
= loga c1 - loga c2
3. loga ck=k loga c
4. loga 
Основное логарифмическое тождество
alog 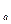 c= c logaab=b
c= c logaab=b
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа 
Показатель степени основания логарифма 
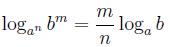 в частности если m = n, мы получаем формулу:
в частности если m = n, мы получаем формулу: 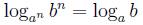
Тригонометрия
Основные тригонометрические тождества
cos2 t + sin2 t = 1
tg α · ctg α = 1
tg α = 
ctg α = 
1 + tg² α = 1/cos² α
1 + ctg² α = 1/sin² α
Тригонометрические функции суммы и разности
(теоремы сложения )

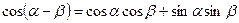

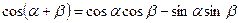

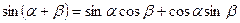



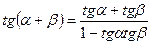

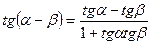 .
.
Формулы двойного угла

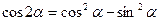

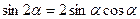

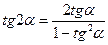 .
.
Тригонометрические функции половинного аргумента

 , откуда
, откуда 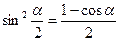

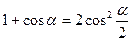 , откуда
, откуда 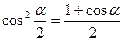
|
|
|

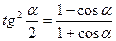 .
.
Преобразование суммы и разности тригонометрических функций
В произведение

 ,
,

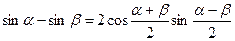 ,
,

 ,
,

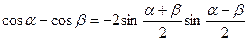 .
.
Преобразование произведений тригонометрических функций в сумму и разность





 .
.
| Решение тригонометрических уравнений | ||||
| a= -1 | a= 0 | a= 1 | Общий вид | |
| sin x = a | x= -p/2 + 2pn, nÎZ | x= pn, nÎZ | x= p/2 + 2pn, nÎZ | x= (-1)n arcsin a + pn, nÎZ |
| cos x = a | x= p + 2pn, nÎZ | x= p/2 + pn, nÎZ | x= 2pn, nÎZ | x= + arccos a + 2pn, nÎZ |
| tg x = a | x= arctg a + pn, nÎZ |
|
|
|


