 |
Тема 1.3. Основы тригонометрии
|
|
|
|
Геометрически угол определяется неоднозначно. Так, например, угол можно определить как часть плоскости, ограниченную двумя лучами, исходящими из одной точки, называемой вершиной угла. Иногда, угол определяется как фигура, образованная двумя лучами, исходящими из одной точки – вершины. В тригонометрии можно использовать как первое, так и второе определения, так как нас больше всего будет интересовать не сам угол, а его мера.
Нам известны следующие единицы измерения величин углов: прямой угол d, градус, минута, секунда: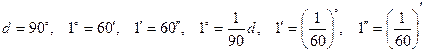 
.
При решении задач механики, астрономии, электротехники и других разделов естествознания и техники широко применяется еще одна единица измерения величин углов – так называемый радиан.
Установим связь между градусным и радианным измерениями некоторых часто встречающихся на практике углов:
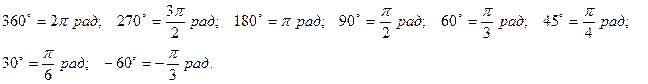Так как 
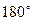соответствует π радианам, то: 
; 
; 
.
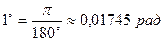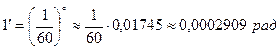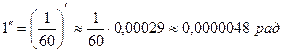Пример. Выразить в радианной мере углы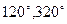 
.
Решение. Очевидно, что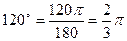 
; 
.
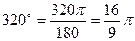Рассмотрим на координатной плоскости единичную окружность, т.е. окружность единичного радиуса с центром в начале координат. Обозначим через P0 точку единичной окружности с координатами (1; 0). Точку P 0 будем называть начальной точкой. Возьмем произвольное число t. Повернем начальную точку на угол t. Получим точку на единичной окружности, которую обозначим через Pt.
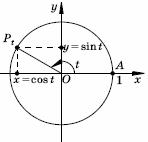
Синусом числаt называется ордината точки Pt, полученной поворотом начальной точки единичной окружности на угол t, косинусом числа t называется абсцисса точки Pt.
Если обозначить координаты точки Pt через x и y, то мы получим x=cos t, y=sin t или можно записать, что точка Pt имеет координаты (cos t, sin t).
Тангенсом числа t называется отношение синуса числа t к его косинусу, т.е. по определению tg t =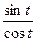 
; котангенсом числа t называется отношение косинуса числа t к его синусу, т.е. по определению ctg t = 
.
|
|
|
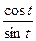Тангенс числа t определен для тех значений t, для которых cos t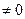 
, а котангенс числа t определен для тех значений t, для которых sin t 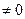. Итак, мы определили правила вычисления тригонометрических функций для числа t.
Из определения тригонометрических функций следует, что sin t cos t могут принимать значения, по модулю не превосходящие 1, т.е. для любых чисел t справедливо неравенство: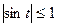 
и 
.
Тангенс числа t и котангенс числа t могут принимать любые значения.
Приведем таблицу значений синуса и косинуса для некоторых значений аргументов, выраженных в радианах и в градусах
| α |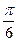 
| 
| 
| 
| 
| 
| 
| 
| |
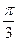
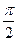
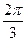
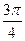
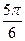
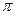
| 0 ْ | 30 ْ | 45 ْ | 60 ْ | 90 ْ | 120 ْ | 135 ْ | 150 ْ | 180 ْ | |
| Sinα |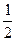 
| 
| 
|
|
|
| |||
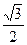
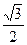
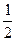
| Cosα |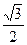
|
|
| -
| -
| -
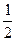
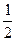
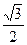
| -1 |
| α |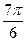 
| 
| 
| 
| 
| 
| 
| 
|
|
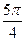
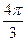
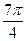
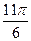
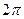
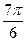
| 210 ْ | 225 ْ | 240 ْ | 270 ْ | 300 ْ | 315 ْ | 330 ْ | 360 ْ | 210 ْ | |
| Sinα | -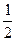
| -
| -
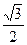
| -1 | -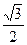
| -
| -
| -
| |
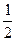
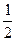
| Cosα | -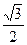
| -
| -
|
|
|
| -
|
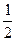
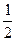
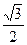
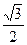
Основное тригонометрическое тождество: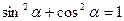 
.
Следствия:
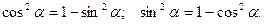
Для тригонометрических функций одного аргумента выполняются также следующие соотношения:
.
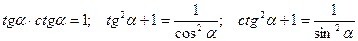Значения тригонометрических функций острых углов можно вычислить по таблицам или при помощи вычислительных приборов (калькуляторов, компьютера и т. п.). Однако при решении практических задач часто возникает необходимость вычислять значения тригонометрических функций для аргумента, большего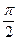 
. Для этой цели существуют так называемые формулы приведения, которые позволяют заменить тригонометрические функции больших значений аргументов тригонометрическими функциями острого угла.
Основными формулами приведения являются следующие
| 
|
| 
|
| 
|
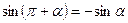
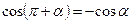
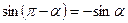
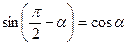
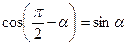
Из основных формул легко вывести и другие формулы приведения:
|
|
|
; 
.
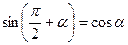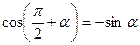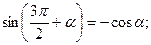
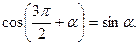
Формулы приведения для тангенса и котангенса получаются как следствия аналогичных формул для синуса и косинуса. Например,
Таким образом, можно вычислить значения всех тригонометрических функций от угла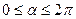 
. В результате получается следующее правило:
Если в формуле приведения угол α вычитается из числа 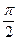или прибавляется к этому числу, взятому нечетное число раз, то приводимая функция меняется на кофункцию; если же число 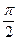взято четное число раз, то название приводимой функции сохраняется. Знак перед приводимой функцией ставится такой, каков знак приводимой функции в соответствующей четверти, если считать угол α острым.
Результат этих вычислений представим в таблице
| Функция | -α |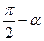 
| 
| 
| 
| 
| 
| 
|
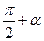
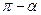
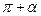
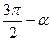
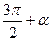
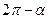
| sin u | - sin α | cos α | cos α | sin α | -sin α | -cos α | -cos α | -sin α |
| cos u | cos α | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α |
| tg u | -tg α | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α |
| ctg u | -ctg α | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α |
Пример. Найти значение cos 315°.
Решение. Ясно, что 
По таблице находим (7-й столбец, 2-я строка):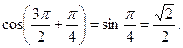 
Можно было бы cos 315° представить как 
и, найти его значение по таблице на пересечении 8-го столбца и 2-й строки.
Пример. Привести к тригонометрической функции острого угла: а) sin 162°; б) cos 830°; в) ctg 2281°.
Решение. а)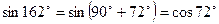 
;
б)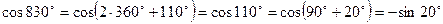 
;
в)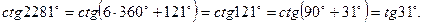 
Тригонометрические функции суммы и разности (теоремы сложения).
Справедливы равенства:
.
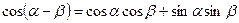
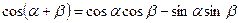
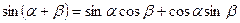
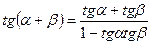
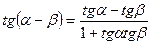Следствие. При β=α из формул суммы тригонометрических функций получим
формулы двойного угла:
.
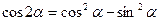
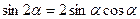
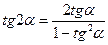Пример. Найти значение cos 15°, используя теоремы сложения.
Решение.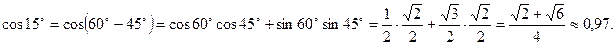 
Пример. Найти tg 45°.
Решение.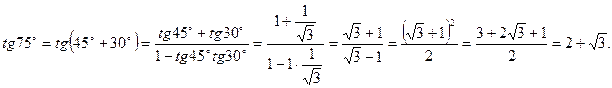 
Тригонометрические функции половинного аргумента.
, откуда 
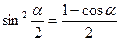
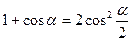, откуда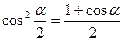 
.
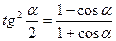Пример. Найти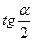 
, если 
, 
.
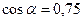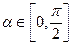Решение.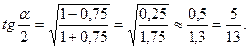 
Пример. Упростите выражение 
.
Решение. Используя формулу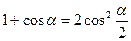 
, получим 
.
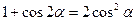Следовательно,
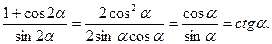
Обратные тригонометрические функции.
Функция, обратная функции y = sin x, рассматриваемой в промежутке -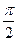 
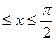, называется арксинусом.
Арксинус обозначается так: x = arcsin y. Областью её определения является промежуток -1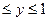 
.
Здесь уже y рассматривается как аргумент, а х – как функция. Чтобы не нарушать привычки в обозначениях (что не имеет принципиального значения), мы переставим буквы и будем писать y = arcsin x.
|
|
|
Таким образом, arcsin x есть дуга (или угол), взятая (взятый) в промежутке
от - 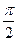до :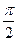
- 
,
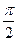
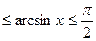cинус которой (которого) равен числу x:
sin (arcsin x) = x.
Например, arcsin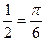 
; arcsin (-1) = - .
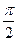Функция, обратная функции y = cos x на сегменте 0 
, называется арккосинусом:
x = arccos y.
Областью определения арккосинуса является промежуток [-1, 1].
Таким образом (поменяв местами роли переменных x и y), заметим, что
arccos х есть дуга (или угол), взятая (взятый) в промежутке от 0 до :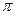
0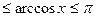 
,
косинус которой (которого) равен x:
cos(arccos x) = x, где -1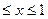 
.
Например, arccos 0= 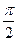, arccos 
.
Функция, обратная функции y = tg x в интервале - 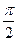< x < 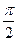, называется арктангенсом:
x = arctg y.
Функция, обратная функции y = ctg x в интервале (0, 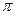), называется арккотангенсом:
x = arcctg y.
Обратные тригонометрические функции используются при решении тригонометрических уравнений.
Тригонометрическими называют уравнения, содержащие неизвестное под знаками тригонометрических функций.
Рассмотрим решения простейших из них:
sin x=a; cos x =a; tg x=a; ctg x=a.
Решить тригонометрическое уравнение – это значит найти все его корни.
Корнем тригонометрического уравнения называется такое значение входящего в него неизвестного, которое удовлетворяет этому уравнению.
Рассмотрим уравнение sin x=a.
При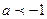 
и 
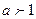это уравнение не имеет решений, так как 
.
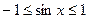При а =1 уравнение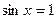 
имеет решения 
.
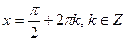При а = -1 уравнение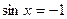 
имеет решения 
.
При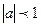 
уравнение sin x=a имеет бесконечное множество решений.
Период синуса равен 2π, поэтому достаточно найти все решения этого уравнения на отрезке длины 2π. Множество решений уравнения sinx=a имеет вид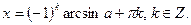 
Пример. Решить уравнение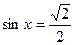 
.
Решение. По формуле получаем:
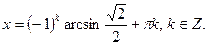
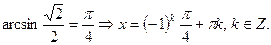
Рассмотрим уравнение cos x =a.
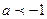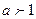При и это уравнение не имеет решений, так как 
.
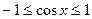При а =1 уравнение 
имеет решения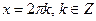 
.
При а = -1 уравнение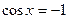 
имеет решения 
.
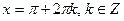При а =0,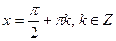 
.
Чтобы записать все решения этого уравнения, необходимо, учитывая периодичность косинуса, прибавить к каждому из найденных значений по 2πk. В итоге получим бесконечное множество решений
|
|
|
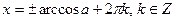. (2)
Пример. Решить уравнение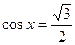 
.
Решение. Так как 
и 
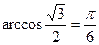, то
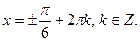
Рассмотрим уравнение tg x=a.
Период функции tg x равен π и каждое из своих значений функция принимает в промежутке длины π один раз. Выберем промежуток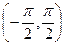 
. По определению арктангенса, на этом промежутке решением уравнения 
будет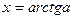 
. Чтобы записать все решения уравнения , необходимо к полученному решению прибавить числа вида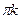 
. Следовательно, уравнение имеет решения
.
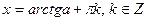Пример. Решить уравнение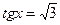 
.
Решение. Так как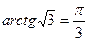 
, то формула (3) в данном случае примет вид
.
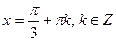Рассмотрим уравнение ctg x=a.
Период функции котангенс равен π, поэтому для нахождения всех решений этого уравнения необходимо найти их на любом отрезке длины π и прибавить к ним числа вида 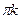. Удобно взять промежуток 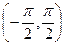. На нем по определению арккотангенса, 
. Следовательно, уравнение 
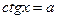имеет решения
.
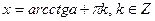Пример. Решить уравнение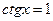 
.
Решение. Так как 
, то формула (4) в данном случае принимает вид
.
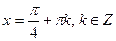Примеры решения тригонометрических уравнений.
Существуют два общих метода решения тригонометрических уравнений – метод подстановки и метод разложения на множители. При решении уравнений методом подстановки очень важен выбор функции, через которую выражаются различные тригонометрические функции одного и того же неизвестного аргумента, входящие в уравнение. Предпочтение необходимо отдавать той функции, которая приводит к рациональному решению.
Рациональные уравнения, в которые входят cosx, sinx и постоянные, записываются в виде
.
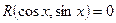Однородным тригонометрическим уравнением первой степени называется уравнение вида
.
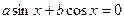Однородным тригонометрическим уравнением второй степени называется уравнение вида
.
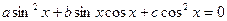Если cosx входит в уравнение лишь в четных степенях, то, заменяя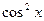 
на 
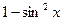, получим рациональное уравнение относительно sinx.
При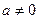 
однородным уравнениям не удовлетворяют те значения неизвестного х, при которых 
. Поэтому, для их решения можно обе части уравнения разделить на cosx или 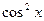; получится уравнение, равносильное данному, рациональное относительно tgx.
При почленном делении на cosx получим уравнение
.
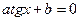При почленном делении на 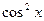получим
.
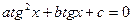Пример. Решить уравнение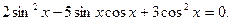 
Решение. Разделив уравнение почленно на 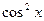, получим
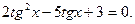
Используем подстановку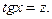 
Тогда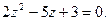 
Корни этого уравнения
.
Следовательно,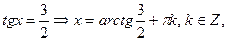 
и 
Любое уравнение вида 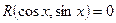можно решить с помощью подстановки 
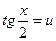, называемой универсальной.
Действительно, если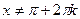 
, то справедливы тождества:
Подставив 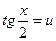, получим 
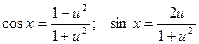, т.е. уравнение левая часть которого является рациональным выражением.
Пример. Решить уравнение 
.
Решение. Выразим sinx и cosx через 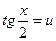, получим
После освобождения от знаменателя и приведения подобных членов получим
|
|
|
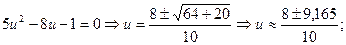
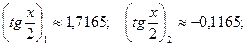
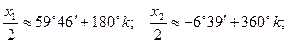
откуда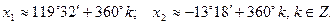 
Рассмотрим примеры решения тригонометрических уравнений методом разложения на множители.
Пример. Решить уравнение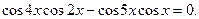 
Решение. Заменим произведения в обоих слагаемых полусуммами косинусов суммы и разности аргументов:
откуда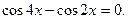 
Заменим разность произведением:
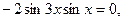
откуда
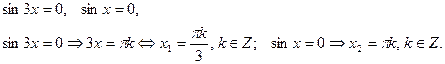
Так как вторая серия решений содержится в первой, то окончательно будем иметь
Пример. Решить уравнение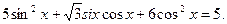 
Решение. Сведем данное уравнение к однородному воспользовавшись тем, что 
, получим
,
что эквивалентно
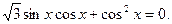
В данном уравнении а =0, т.е. отсутствует член 
Здесь уже делить обе части уравнения на 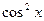нельзя, так как те значения х, при которых 
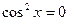, удовлетворяют полученному нами уравнению. Деление на 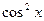приведет к потере корней, поэтому разложим левую часть уравнения на множители:
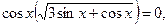
откуда 
Первое из этих уравнений имеет решения
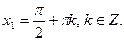
Чтобы найти решение второго уравнения, разделим его почленно на cosx и получим
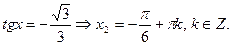
Пример. Решить уравнение 
Решение. Перенесем второй член левой части уравнения в право, получим
Мы уже знаем, что если тангенсы равны, то их аргументы разнятся на величины π k, поэтому
|
|
|
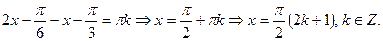
