 |
НЕДЕЛЯ 5. Тема «Средние величины и показатели вариации признака»
|
|
|
|
Метод средних величин - основа основ статистического анализа, так как на понятии средней величины базируются все прочие специфические методы статистики: изучение вариации признаков, выборочное наблюдение, изучение структуры совокупности и динамики показателей, в том числе и с помощью индексного метода.
Виды средних величин и способы их вычисления:
- Степенные (средняя арифметическая, гармоническая, геометрическая)
- Структурные (мода и медианна).
Выбор средней величины:
1.Средняя арифметическая простая применяется в случае, если индивидуальное значение признака у единиц совокупности не повторяется или встречается один раз или одинаковое число раз, т.е. когда средняя рассчитывается по формуле:
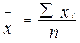
где х i - варианты (отдельные значения признака);
п - число единиц в совокупности.
2.Средняя арифметическая взвешенная. Когда отдельное значение изучаемого признака встречается несколько раз у единиц изучаемой совокупности, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетной формуле: средней взвешенной:
где fi - частоты, показывающие, сколько раз встречается значение признака х i y единиц совокупности.
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
В интервальных рядах значение признака задано в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному. В качестве вариантов х i используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
|
|
|
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
3.Средняя гармоническая – величина обратная средней арифметической.
Она рассчитывается в тех случаях, когда веса fi не заданы непосредственно, а входят как сомножитель в один из имеющихся показателей. Средняя гармоническая рассчитывается по формуле:
где wi - произведения вариант на соответствующие им частоты.
4. Средняя геометрическая – это средняя из отношений, представленных в виде геометрической прогрессии. Средняя геометрическая используется в расчетах среднегодовых темпов роста и рассчитывается по формуле:
где 
- цепные коэффициенты роста.
К структурным средним относят: моду и медиану.
Мода (Мо) - это значение варьирующего признака, наиболее часто встречающееся в данном ряду. Модой в дискретном ряду является вариант, имеющий наибольшую частоту. В интервальном же вариационном ряду моду определяют по формуле:
где: 
- нижняя граница модального или медианного интервала;
- величина интервала;
- частота, предшествующая модальному интервалу;
- частота, следующая за модальным интервалом;
- частота модального интервала
Медиана (Ме) - это численное значение признака у той единицы изучаемой совокупности, которая находится в середине ранжированного ряда.
Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для медианы равна половине объема совокупности. Для интервального ряда в этом случае определяется только интервал, само значение определяется по формуле:
|
|
|
где 
- начальное значение медианного интервала;
- величина интервала;
N - объем совокупности;
- накопленная частота в интервале, предшествующем медианному;
- частота медианного интервала.
Для измерения вариации признака применяются различные абсолютные и относительные показатели.
К абсолютным показателям вариации относятся:
1. Размах вариации– это разность между максимальным и минимальным значениями признака определяется по формуле:
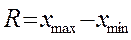
где х max, х min - максимальное и минимальное значения признака.
Размах вариации показывает, в каких пределах колеблется размер признака, образующего ряд распределения.
2. Среднее абсолютное отклонение - средняя из абсолютных значений отклонений отдельных вариант от средней определяется по формуле:
(простая),
(взвешенная)
3. Дисперсия - средняя из квадратов отклонений вариантов значений признака от их средней величины определяется по формуле:
(простая)
(взвешенная)
4. Среднее квадратичное отклонение представляет собой корень квадратный из дисперсии, показывает насколько в среднем колеблется величина признака у единиц изучаемой совокупности определяется по формуле:
s =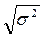 
Чем меньше среднее квадратичное отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
5. Коэффициент вариации, который показывает среднее отклонение от среднего значения признака в процентах определяется по формуле:
Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Пример выполнения задания
Распределение результатов хронометража деятельности операций при обработке детали одним рабочим характеризуется данными таблицы 17:
Таблица 17
Длительность операции при обработке деталей, сек.
| Длительность операции | 47 -49 | 49 -51 | 51 -53 | 53 -55 | 55 -57 | 57- 59 | 59 -61 | 61 -63 | 63 -65 | 65 -67 |
| Число операций | 6 | 13 | 15 | 20 | 15 | 11 | 8 | 5 | 4 | 2 |
|
|
|
Определить:
1) среднюю длительность операции;
2) размах вариации;
3) дисперсию;
4) среднее квадратичное отклонение;
5) коэффициент вариации;
6) моду и медиану.
Решение:
Суммы квадратов отклонений значений признаков от средней величины представлены в таблице 18
Таблица 18
Расчет абсолютных показателей вариации
| Середина интервала х i | Число операций, fi | х i ×fi | х i - 
| (х i -  )2
| (х i - ) 2 fi
|
| 48 | 6 | 288 | -7,09091 | 50,28099 | 301,6859 |
| 50 | 13 | 650 | -5,09091 | 25,91736 | 336,9257 |
| 52 | 15 | 780 | -3,09091 | 9,553719 | 143,3058 |
| 54 | 20 | 1080 | -1,09091 | 1,190083 | 23,80166 |
| 56 | 15 | 840 | 0,909091 | 0,826446 | 12,39669 |
| 58 | 11 | 638 | 2,909091 | 8,46281 | 93,09091 |
| 60 | 8 | 480 | 4,909091 | 24,09917 | 192,7934 |
| 62 | 5 | 310 | 6,909091 | 47,73554 | 238,6777 |
| 64 | 4 | 256 | 8,909091 | 79,3719 | 317,4876 |
| 66 | 2 | 132 | 10,90909 | 119,0083 | 238,0166 |
| Итого, S | 99 | 5454 | 1898,182 |
1) определение средней величины признака 
по формуле средней арифметической взвешенной:
= 5454 / 99 = 55,1
2) размах вариации (R) = Хмакс. – Хмин. = 67 – 47 = 20
3) дисперсия 
= 1898,182 / 99 = 19,173
4) среднее квадратичное отклонение 
5) коэффициент вариации 
= 4,44 ×100% / 55,1 = 8 %
6) мода – значения признака, наиболее часто встречающееся в совокупности
Наибольшая частота соответствует интервалу от 53 до 55. Число операций равно 20. Это модальный интервал, для расчета которого используется формула:
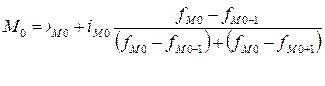
Мо = 53 + 2 × (20-15) = 53
(20-15)+(20-15)
Наиболее часто встречающаяся длительность операции 53 секунды.
Определение медианного интервала. Это интервал, накопленная частота которого больше или равна половине суммы частот (99/2 = 50), то есть медианным будет интервал от 53 до 55. Накопленные частоты представлены в таблице 19.
Таблица 19
Накопленные частоты
| Интервал | Частоты fi | Накопленные частоты S |
| 47-49 | 6 | 6 |
| 49-51 | 13 | 19 |
| 51-53 | 15 | 34 |
| 53-55 | 20 | 54 |
| 55-57 | 15 | 69 |
| 57-59 | 11 | 80 |
| 59-61 | 8 | 88 |
| 61-63 | 5 | 93 |
| 63-65 | 4 | 97 |
| 65-67 | 2 | 99 |
| Сумма | 99 |
Определение медианы:
=53 + 2 × (49,5 -34) / 20 = 54,55
Половина операций имеют длительность меньше 54,55 секунд.
|
|
|
Половина - больше 54,55 секунд.
Задание 1
На основе данных таблицы 20 определить изменение средней цены в абсолютных и относительных величинах.
Таблица 20
Цены на мясные продукты
| Продукт | Декабрь 2008г. | Январь 2009 г. | ||
| Цена за 1кг, тенге | Выручка, тенге | Цена за 1кг, тенге | Количество, кг. | |
| Говядина Курица Рыба | 550 500 400 | 990000 600000 340000 | 680 650 500 | 360 300 185 |
Задание 2
На основе данных таблицы 21 определить:
1) среднюю посевную площадь;
2) среднюю урожайность;
3) средний валовой сбор.
Таблица 21
Показатели деятельности бригад за 2007 год
| № бригады | Урожайность ц/га, хi | Посевная площадь, га, fi | Валовой сбор, ц,хi fi |
| 1 2 3 | 17,8 16,5 15,4 | 160 100 140 | 2848 1650 2156 |
| Итого: | 49,7 | 400 | 6654 |
Задание 3
На основе данных таблицы 22 определить индекс средней месячной заработной платы
Таблица 22
Распределение зарплат продавцов
|
Секция | март | октябрь | ||||
| Средняя зарплата, р. | Число продавцов | Фонд оплаты труда, р. | Средняя зарплата, р. | Фонд оплаты труда, р. | Число продавцов | |
| 1 2 3 | 5850 7100 6980 | 10 15 10 | 58 500 106 500 69 800 | 6900 8200 7000 | 55200 49200 28000 | 8 6 4 |
| - | 35 | 234800 | - | 132400 | 18 | |
Задание 4
На основе данных таблицы 23 определить:
1) абсолютное и относительное изменение себестоимости единицы продукции;
2) среднюю себестоимость единицы продукции;
3) абсолютную экономию общей себестоимости.
Таблица 23
Выработка и себестоимость продукции «А»
|
| Базисный период | Отчетный период | ||||
| Продукция шт., q0 | Себестоимость единицы, тенге, z0 | Затраты, тенге z0q0 | Продукция шт., q1 | Себестоимость единицы, тенге, z0 | Затраты, тенге, z1q1 | |
| № 1 | 4000 | 30 | 120000 | 4500 | 25 | 112500 |
| №2 | 3800 | 32 | 121600 | 4200 | 30 | 126000 |
| Итого | 7800 | 241600 | 8700 | 238500 | ||
Задание 5
На основе данных таблицы 24 определить изменение средней урожайности в абсолютных и относительных величинах.
Таблица 24
Динамика посевной площади и урожайности пшеницы
| № предприятий | 2006 г. | 2007 г. | |||
| Урожайность, ц\га | Посевная площадь, га | Урожайность, ц\га | Валовой сбор, ц. | Посевная площадь, га | |
| 1 2 3 | 15,0 17,3 16,5 | 120 75 105 | 16,1 16,8 15,4 | 4044,6 2672,0 3326,4 | 251,2 159 216 |
| Итого: | - | 300 | - | 10043 | 626,2 |
Задание 6
На основе данных таблицы 25 определить средний размер незавершенного строительства за отчетный год.
Таблица 25
Остатки незавершенного строительства, млн. тенге
| Показатель | 1.01.08 г. | 1.04.08 г. | 1.07.08 г. | 1.10.08 г. | 1.01.09 г. |
| Размер незавершенного строительства | 250 | 345 | 355 | 285 | 210 |
Задание 7
На основе данных таблицы 26 определить по автоколоннам в целом:
1) среднюю себестоимость тонно-километра;
|
|
|
2) среднее суточное число тонно-километров, сделанных автомашиной;
3) среднее число работающих автомашин в автоколоннах.
Примечание: число дней работы во всех автоколоннах одинаково - 22 дня.
Таблица 26
Показатели деятельности трех автоколонн
| Автоколонна | Затраты на перевозку всех грузов, млн. руб. | Себестоимость одного тонно-километра, тыс. руб. | Средний суточный грузооборот автомашины, т-км |
| 1 | 210 | 0,7 | 250 |
| 2 | 228 | 0,6 | 300 |
| 3 | 258 | 0,5 | 350 |
Задание 8
На основе данных таблицы 27 определить по трем предприятиям за период:
1) среднее число отработанных одним рабочим дней;
2) среднюю дневную выработку одного рабочего;
3) среднюю квартальную выработку;
4) средние затраты на 1 рубль произведенной продукции.
Таблица 27
Показатели деятельности предприятия
| № п/п | Число рабочих, чел. | Среднее число дней, отработанных одним рабочим | Средняя дневная выработка 1 рабочего, тыс. руб./чел.-дн. | Затраты на 1 рубль произведенной продукции, коп. |
| 1 | 500 | 60 | 25,0 | 90,6 |
| 2 | 1000 | 64 | 30,0 | 85,4 |
| 3 | 900 | 62 | 28,0 | 82,0 |
Задание 9
На основе данных таблицы 28 определить:
1) средние затраты на 1 рубль товарной продукции;
2) среднюю дневную выработку рабочего, тыс. руб. чел.-дн.;
3) среднесписочное число работников, чел.;
4) среднее число дней отработанных за квартал одним рабочим.
Таблица 28
Показатели деятельности предприятия
| Предприятие | Затраты производства | Средняя дневная выработка рабочего, тыс. руб. | Среднее число рабочих дней в квартале | |
| Общие, тыс.руб. | На 1 руб. товарной продукции, коп. | |||
| 1 | 68,0 | 90,6 | 25,5 | 60 |
| 2 | 163,5 | 85,4 | 32,2 | 64 |
| 3 | 128,5 | 82,0 | 28,7 | 62 |
Задание 10
На основе данных таблицы 29 определить в целом по предприятию средние значения часовой, дневной и месячной выработки одного рабочего.
Таблица 29
Распределение средней выработки по изделиям
| Изделие | Выработано, млн. руб. | Средняя выработка, тыс.руб./чел. | ||
| в час | в день | в месяц | ||
| 1 | 230,6 | 2,2 | 13,6 | 310 |
| 2 | 300,0 | 1,8 | 10,8 | 250 |
| 3 | 295,6 | 2,0 | 13,0 | 312 |
Задание 11
На основе данных таблицы 30 рассчитать среднюю зарплату рабочих.
Таблица 30
Распределение работников предприятия по уровню заработной платы
| Интервал по зарплате, долл. | Число рабочих в группе, чел. |
| 180-200 | 10 |
| 200-400 | 30 |
| 400-600 | 50 |
| 600-800 | 60 |
| 800-1000 | 145 |
| 1000-1200 | 110 |
| 1200-1400 | 80 |
| 1400-1600 | 15 |
| Итого: | 500 |
Задание 12
На основе данных таблицы 31 определить среднюю заработную плату рабочих по трем предприятиям:
Таблица 31
Распределение работников предприятий по уровню среднемесячной заработной платы
| Предприятие | Среднемесячная зарплата рабочих, тыс. тенге | Израсходованный за месяц фонд зарплаты рабочих, млн. тенге |
| 1. | 66 | 93,7 |
| 2. | 54,6 | 84,8 |
| 3. | 78,4 | 105,3 |
Задание 13
На основе данных таблицы 32 определить среднюю трудоемкость изготовления деталей.
Таблица 32
Распределение затрат времени на изготовление одной детали
| Затраты времени на изготовление одной детали, мин. | 20-21 | 21-22 | 22-23 | 23-24 |
| Число изготовленных деталей | 6 | 13 | 10 | 7 |
Задание 14
На основе данных таблицы 33 определить:
1) среднюю величину;
2) коэффициент вариации;
3) моду и медиану.
Таблица 33
Структура рабочих по затратам времени на одну деталь
| Затраты времени на одну деталь, мин | Удельный вес рабочих, % |
| до 24 | 2 |
| 24-26 | 12 |
| 26-28 | 34 |
| 28-30 | 40 |
| 30-32 | 10 |
| 32-34 | 2 |
Задание 15
На основе данных таблицы 34 определить:
1) среднюю величину;
2) коэффициент вариации;
3) моду и медиану.
Таблица 34
Распределение территорий РФ по стоимости валового регионального продукта
| Группы территорий РФ по стоимости ВРП на 1-го работника, тыс.руб. | Число территорий, fi |
| От 12,5 до 22,4 | 16 |
| От 22,4 до 32,3 | 32 |
| От 32,3 до 42,2 | 14 |
| От 42,2 до 52,1 | 8 |
| От 52,1 и более | 7 |
| Итого: | 76 |
Задание 16
На основе данных таблицы 35 определить:
1) среднюю величину;
2) коэффициент вариации;
3) моду и медиану.
Таблица 35
Распределение рабочих по уровню месячной заработной платы
| Заработная плата, тыс. руб. | Число рабочих, чел. | Заработная плата, тыс. руб. | Число рабочих, чел. |
| 5-6 | 12 | 7-8 | 20 |
| 6-7 | 60 | 8-9 | 8 |
Задание 17
На основе данных таблицы 36 определить:
1) среднюю величину;
2) коэффициент вариации;
3) моду и медиану.
Таблица 36
Структура рабочих по продолжительности отпусков
| Продолжительность отпусков, хi | В процентах (частость) |
| 15 | 0 |
| 18 | 17 |
| 21 | 2 |
| 23 | 1 |
| 24 | 70 |
| 30 | 10 |
| Итого: | 100 |
Вопросы для самопроверки:
1. Что такое средняя величина признака и какова ее сущность?
2. Простая средняя арифметическая и область ее применения.
3. Средняя арифметическая взвешенная и область ее применения.
4. Средняя гармоническая, ее виды и область применения.
5. Свойства средней величины.
6. Что такое общий размах вариации, линейное отклонение и его средняя величина?
7. Что такое дисперсия и среднее квадратическое отклонение?
8. Что такое коэффициент вариации? Его значение в анализе распределения?
9.Что такое «мода» и «медиана» в рядах распределения? Их сущность и значение для анализа распределения единиц совокупности внутри размаха вариации.
|
|
|
