 |
НЕДЕЛЯ 6. Тема «Выборочное наблюдение»
|
|
|
|
Выборочное наблюдение - несплошное наблюдение, при котором статистическому обследованию подвергаются не все единицы изучаемой совокупности, а лишь часть, отобранная в определенном порядке.
Характеристики генеральной и выборочной совокупностей.
Основные понятия при выборочном наблюдении:
Генеральная совокупность (N) - совокупность единиц, из которых производится отбор (все крестьянские хозяйства области)
Выборочная совокупность (n) - совокупность отобранных единиц (отобранные в случайном порядке несколько крестьянских хозяйств)
Генеральная средняя (
) - средний размер в генеральной совокупности (средняя посевная площадь в генеральной совокупности)
Выборочная средняя (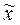
) - средний размер в выборочной совокупности
Генеральная доля (p = М/N) - доля единиц, обладающих тем или иным признаком в генеральной совокупности (доля к/х с посевной площадью от 1000 до 2000 га в генеральной совокупности)
Выборочная доля (w = m/n) - доля единиц, обладающих тем или иным признаком в выборочной совокупности (доля к/х с посевной площадью от 1000 до 2000 га в выборочной совокупности)
Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (средней 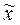и доли w) получить достоверные суждения о показателях средней «
»и доли «p» в генеральной совокупности.
Расхождения между выборочными и генеральными характеристиками (средней и доли) называют ошибками.
Средняя ошибка выборочной средней (µ) определяется по формулам:
- для повторного отбора
- для бесповторного отбора
где s2 – дисперсия признака в генеральной совокупности
Предельная ошибка выборочной средней определяется по формуле:
|
|
|
где t – коэффициент доверия, определяемый по интегральной функции Лапласа при заданной доверительной вероятности.
Степень вероятности и коэффициенты доверия
| (t)Р | 0,683 | 0,95 | 0,954 | 0,99 | 0,997 |
| t | 1 | 1,96 | 2 | 2,58 | 3 |
Средняя ошибка выборочной доли ( µω) определяется по формулам:
- для повторного отбора;
- для бесповторного отбора
Предельная ошибка выборочной доли определяется по формуле:
Генеральная средняя (
) отличается от выборочной средней (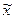
) на величину предельной ошибки выборки:
Это означает: с заданной вероятностью можно утверждать, что значение генеральной средней можно ожидать в пределаx от 
до 
, то есть что доверительный интервал (
) с заданной вероятностью заключает в себе генеральную среднюю.
Генеральная доля (р) отличается от выборочной доли (w) на величину предельной ошибки выборки:
Зная выборочную долю признака (w) и предельную ошибку выборки (
), можно определить границы, в которых заключена генеральная доля p: 
. Это означает: с заданной вероятностью можно утверждать, что значение генеральной доли можно ожидать в пределаx от 
до 
, то есть что доверительный интервал (
)с заданной вероятностью заключает в себе генеральную долю.
Пример выполнения задания
Произведена 30%-ная механическая выборка для изучения сменой выработки рабочих предприятия.
Выборка дала следующие результаты (таблица 37):
Таблица 37
Распределение рабочих по сменной выработке, штук
| Группы рабочих по сменной выработке, штук | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 |
| Число рабочих | 4 | 16 | 24 | 11 | 5 |
Определить:
1) пределы значений среднего уровня сменной выработки рабочих с вероятностью 0,954;
2) пределы значений доли рабочих, вырабатывающих за смену свыше 50 изделий, с вероятностью 0,997.
Решение:
Таблица 38
Расчет дисперсии
| Группы рабочих по сменной выработке, штук | Середина интервала, xi | Число рабочих fi | хi fi | (хi-  )2fi
|
| 21-30 | 25,5 | 40 | 1020 | 5941,406 |
| 31-40 | 35,5 | 16 | 568 | 76,5625 |
| 41-50 | 45,5 | 24 | 1092 | 1464,844 |
| 51-60 | 55,5 | 11 | 610,5 | 3490,137 |
| 61-70 | 65,5 | 5 | 327,5 | 3867,676 |
| Итого: | 96 | 3618 | 14840,63 | |
| Средняя | 37,69 | 154,6 |
|
|
|
1. Определение выборочной средней
(
) 
= 3618 / 96 =37,69 штук;
2. Определение генеральной совокупности
N = 96 / 0,3 = 320 рабочих
3. Определение средней ошибки выборочной средней для бесповторного отбора
= 
= 1,06
4. Определение предельной ошибки выборочной средней
= 2 × 1,06 = 2,12.
Вывод: С вероятностью 95,4% можно утверждать, что средний уровень сменной выработки в генеральной средней находится в пределаx:
от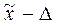 
до 
от 37,69 - 2,12 до 37,69 + 2,12 т.е. от 35,57 до 39,81 штук.
5. Определение выборочной доли рабочих, вырабатывающих за смену свыше 50 изделий:
W = m/n = 16: 96 = 0,167
6. Определение средней ошибки выборочной доли для бесповторного отбора
= 
= 0,031849
7. Определение предельной ошибки выборочной доли
= 3×0,031849 = 0,095547
8. Определение доверительного интервала, т.е. генеральной доли рабочих, вырабатывающих за смену свыше 50 изделий
от 0,166667 - 0,095547 до 0,166667 + 0,095547 или от 0,07112 до 0,262213.
Умножив полученные данные на 320, получается от 23 до 84 человек.
Задание 1
В государственном учреждении из 300 служащих проведена 20%-ная механическая выборка с целью определить фактическую продолжительность рабочего дня. В результате установлено, что в выборке у 6 человек потери рабочего времени превышают 30 минут в день. Определите с вероятностью 0,683 в каких границах находится доля таких служащих по всему учреждению.
Задание 2
Требуется проверить партию деталей на соответствие стандарту путем случайной бесповторной выборки. Какой объем выборки необходим в партии из 10 000 деталей, чтобы с вероятностью 0,954 предельная ошибка выборочной доли не превысила 2%, если по данным пробного исследования доля нестандартной продукции составляет около 8%?
Задание 3
В городе проживает 12 000 семей. Методом бесповторного отбора обследовано 480 семей. Из них 120 семей – многодетные. С вероятностью 0,954 установите пределы, в которых находится доля многодетных семей во всем городе.
Задание 4
При изучении естественной убыли произведено 3%-ное выборочное обследование партии хранящегося на складе сырья. В результате анализа установлено распределение образцов полученных методом механической выборки, представленные в таблице 39.
|
|
|
Таблица 39
Распределение образцов сырья по проценту естественной убыли в выборке
| Процент естественной убыли | Количество образцов |
| До 5 5-7 7-9 9-11 11 и выше | 4 16 28 37 15 |
| Итого: | 100 |
Определить для генеральной совокупности:
1) с вероятностью 0,997 возможные пределы доли сырья с естественной убылью выше 11%;
2) с вероятностью 0,997 возможные пределы среднего процента естественной убыли.
Задание 5
В результате обследования возраста рабочих методом случайного бесповторного отбора в выборочной совокупности из 1000 человек получены данные, представленные в таблице 40:
Таблица 40
Распределение рабочих по возрасту
| Возраст рабочих, лет | до 30 | 30-40 | 40-50 | 50-60 | свыше 60 |
| Число рабочих, человек | 8 | 22 | 10 | 6 | 4 |
Определить с вероятностью 0,997 пределы, в которых находится средний возраст рабочих.
Задача 6
При проверке продукции на таможне средняя влажность в выборке составила 6% при средней ошибке выборки 0,3%. С вероятностью 0,997 (t = 3) определить границы влажности продукции во всей импортируемой партии (по формуле случайного повторного отбора).
Задание 7
На предприятии работает 1250 человек. Для определения средней зарплаты было выбрано 20% и рассчитана средняя зарплата в 14600 тенге. Определить границы средней зарплаты по всему АО с вероятностью 0,997.
Задание 8
Произведена 30%-ная механическая выборка для изучения величины сменной выработки токарей завода. Результаты выборки представлены в таблице 41.
Таблица 41
Распределение рабочих по величине выработки, штук
| Группы рабочих по величине выработки, штук | 71-80 | 81-90 | 91-100 | 101-110 | 111-120 |
| Число рабочих | 4 | 16 | 24 | 11 | 5 |
Определить:
1) пределы значений среднего уровня сменной выработки токарей с вероятностью 0,954;
2) пределы значений доли токарей, вырабатывающих за смену свыше 100 деталей, с вероятностью 0,683.
|
|
|
Задание 9
В целях контроля за соблюдением норм расхода сырья, проведено выборочное обследование партии готовой продукции.
При механическом способе отбора 2 % изделий получены данные о весе обследованных единиц, представленные в таблице 42.
Таблица 42
Распределение образцов продукции по расходу сырья
| Вес изделия, грамм | Число образцов, штук |
| до 2000 | 6 |
| от 2000 до 2050 | 20 |
| от 2050 до 2100 | 60 |
| свыше 2150 | 4 |
При условии, что к стандартной продукции относятся изделия с весом от 2000 до 2150 грамм, установите для всей партии:
1) с вероятностью 0,954 возможны пределы удельного веса стандартной продукции;
2) с вероятность 0,997 возможные пределы среднего веса одного изделия в генеральной совокупности.
Задание 10
При выборочном обследовании 0,5 % партии кирпича (случайная бесповоротная выборка) установлено, что 320 единиц из обследованных 400 образцов отнесены к стандартной продукции.
Распределения образцов по весу приведено в таблице 43.
Таблица 43
Распределение образцов по весу
| Вес изделия, г. | Число образцов, шт. |
| до 3000 от 3000 до 3100 от 3100 до 3200 от 3200 до 3300 свыше 3300 | 10 50 190 130 20 |
Установить для всей партии продукции:
1) с вероятностью 0,997 возможные пределы удельного веса стандартной продукции;
2) с вероятностью 0,954 возможные пределы среднего веса изделия.
Задание 11
Произведено выборочное обследование длительности производственного стажа рабочих. В выборку было взято 200 рабочих из общего количества в 1000 человек. Результаты выборки приведены в таблице 44:
Таблица 44
Распределение рабочих по продолжительности стажа
| Продолжительность стажа в годах | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 |
| Число рабочих | 40 | 80 | 50 | 20 | 10 |
Определить:
1) с вероятностью 0,997 возможные пределы колебаний средней продолжительности стажа всех рабочих;
2) Какое число рабочих надо взять в выборку, чтобы ошибка не превышала 0,5 года на основе приведенных выше показателей?
Задание 12
Произведено выборочное обследование длительности производственного стажа рабочих в выборку было взято 100 рабочих из общего количества в 1000 человек. Результаты выборки представлены в таблице 45:
Таблица 45
Распределение рабочих по продолжительности стажа
| Продолжительность стажа в годах | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 |
| Число рабочих, человек | 20 | 40 | 25 | 10 | 5 |
Определить:
1) с вероятностью 0,997 возможные пределы колебаний средней продолжительности стажа всех рабочих;
2) Какое число рабочих надо взять в выборку, чтобы ошибка не превышала 0,5 года?
Задание 13
В районе выборочно обследована тысяча семей по уровню доходов путем 2%-ной случайной бесповторной выборки. Среди обследованных 300 семей оказались малообеспеченными. Требуется с вероятностью 0,997 определить границы для доли малообеспеченных семей по всему району.
|
|
|
Задание 14
АО «Казахтелеком» предполагает провести выборочное обследование для определения удельного веса телефонных разговоров, превышающих 5 минут. По данным пробного обследования доля таких разговоров составляет около 40%. Сколько телефонных разговоров надо обследовать на основе случайной повторной выборки, чтобы ошибка для доли разговоров длительностью более 5 минут не превысила 10% с вероятностью 0,954?
Задание 15
В акционерном обществе трудовой коллектив насчитывает 1 250 человек. С целью определить средний доход на 1 работника была проведена 20%-ная механическая выборка. Установлено, что средний доход на 1 работника за месяц составляет в выборке 14 600 тенге при среднем квадратическом отклонении 4 672 тенге. Определите границы среднего дохода на 1 работника по всему АО с вероятностью 0,997.
Задание 16
В государственном учреждении из 300 служащих проведена 20%-ная механическая выборка с целью определить фактическую продолжительность рабочего дня. В результате установлено, что в выборке у 6 человек потери рабочего времени превышают 30 минут в день. Определите с вероятностью 0,683 в каких границах находится доля таких служащих по всему учреждению.
Задание 17
Требуется проверить партию деталей на соответствие стандарту путем случайной бесповторной выборки. Какой объем выборки необходим в партии из 12 000 деталей, чтобы с вероятностью 0,954 ошибка выборочной доли не превысила 2%, если по данным пробного исследования доля нестандартной продукции составляет около 10%.
Задание 18
В процессе технического контроля из партии готовой продукции случайным бесповторным отбором проверено 50 изделий, среди которых оказались 4 изделия, не соответствующих стандартам качества. Можно ли утверждать с вероятностью 0,954, что доля нестандартной продукции не превысит 9%, если выборка составляет 10% всей партии?
Задание 19
Для определения среднего размера вклада в филиалах банка предполагается провести бесповторную выборку из 35 520 лицевых счетов. По данным предыдущего обследования установлено, что среднее квадратическое отклонение размера вклада составляет 20 тыс. тенге. Определите необходимый объем выборки при условии, что ошибка выборки не превысит 1,5 тыс. тенге с вероятностью 0,954.
Задание 20
Из 5 000 правонарушителей было обследовано 500 человек методом случайного бесповторного отбора. Установлено, что из них 300 человек выросли в неблагополучных семьях. С вероятностью 0,997 определить долю правонарушителей, выросших в неблагополучных семьях, в генеральной совокупности.
Вопросы для самопроверки:
1. Что такое генеральная и выборочная совокупности? Их отношение?
2. Виды выборки и способы отбора единиц в выборку.
3. Ошибки каких показателей должны вычисляться при оценке точности выборочного наблюдения?
4. Средняя ошибка, предельная ошибка, доверительный интервал.
5. Как связана величина доверительного интервала с вероятностью?
6. Как влияет способ отбора единиц на дисперсию в формуле ошибки?
7. Как влияет способ отбора единиц на учет доли выборки в формуле ошибки?
НЕДЕЛЯ 7. Тема «Индексы»
Индекс – относительный показатель, который получают при сопоставлении уровней сложных социально-экономических показателей для соизмерения их в пространстве, во времени и с планом.
Классификация индексов
1. По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы.
Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности (например, изменение выпуска легковых автомобилей определенной марки). Например, индивидуальный индекс цены определяется по формуле:
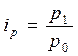
где р1 и p0 – цены в отчетном и базисном периоде.
Он показывает, как цена на данный товар в текущем периоде изменилась по сравнению с ценой этого же товара в базисном периоде.
Аналогичным образом строятся индивидуальные индексы сравнения с плановыми или нормативными значениями, например индекс выполнения плана по объему продукции определяется по формуле:
где q пл. - количество единиц данного вида продукции, предусмотренное планом.
В числителе и знаменателе территориальных индексов находятся значения показателя, относящиеся к двум сравниваемым территориям, например индивидуальный территориальный индекс цен на определенный товар имеет вид:
где рА, рВ - цена данного товара соответственно на территориях А и В.
Сводный индекс отражает изменение по всей совокупности элементов сложного явления и обозначается I. Сводный индекс состоит из: индексируемой величины, характер изменения которой определяется 
и соизмерителя, который называется весом.
Например, сводный индекс цен определяется по формуле:
веса
где р 0 и р 1 - себестоимость единицы продукции данного вида соответственно в базисном и отчетном периодах;
q 1- физический объем выпуска данного вида продукции в отчетном периоде.
Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились.
Сводный индекс физического объёма товарооборота определяется по формуле:
веса
Индексируемая величина – количество товаров в натуральном выражении. Его применение дает возможность оценить изменение физического объема продаж при сохранении цен неизменными. Цены в этом индексе фиксируются на уровне базисного периода.
2. По базе сравнения выделяют: динамические, территориальные индексы и индексы выполнения плана.
Динамические индексы рассчитываются как базисным, так и цепным способами. Цепной способ – текущий уровень показателя сопоставляют с уровнем показателя за предшествующий период. При базисном способе текущий уровень показателя сопоставляют с уровнем показателя за базисный период.
Территориальные индексы характеризуют уровни сложных показателей, характеризующих различные территории или совокупности (одноименные показатели).
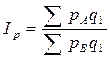
где рА и p В – цены на одни и те же товары в различных регионах.
Территориальные индексы выражают соотношение сложных экономических явлений в пространстве по городам, областям, районам, странам и т.д.
Индекс выполнения плана показывает изменение текущего уровня сложного показателя по сравнению с запланированным уровнем анализируемого показателя.
где z1 q1 –общая себестоимость каждого изделия в отчётном периоде;
z пл., q 1 – сумма затрат на изделие, выпущенное в отчетном периоде по плановой себестоимости.
3. По составу явления различают: индексы постоянного (фиксированного) состава и индексы переменного состава.
Индексом постоянного состава называется индекс, характеризующий динамику средних величин при одной и той же фиксированной структуре совокупности. То есть, в индексе постоянного состава изменяется только индексированная величина, а веса остаются неизменными.
Общий вид индекса постоянного состава определяется по формуле:
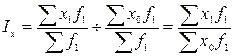
Относительную величину, характеризующую динамику двух средних показателей для однородной совокупности называют индексом переменного состава.
Индекс переменного состава характеризует общее изменение средней, как в результате изменения индивидуальных значений индексируемой величины, так и в результате изменения структуры совокупности (весов) определяется по формуле:
где х1 и х0 – уровни осредненного показателя в отчётном и базисном периодах;
f 1 и f 0 – веса (частоты) осредненного показателя в отчетном и базисном периодах.
Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов, как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчётную структуру, к фактической средней этого показателя в базисном периоде определяется по формуле:
или
Пример выполнения задания
В таблице 63 приведены данные о товарообороте в октябре и декабре и изменении цен:
Таблица 63
Изменение товарооборота и цен
| Товарные группы | Товарооборот, тыс. тенге | Изменение цен в декабре, % | |
| За октябрь, p0q0 | За декабрь, p1q1 | ||
| А Б В | 240 430 500 | 276 559 625 | +30 +60 +40 |
| Итого: | 1170 | 1460 | |
Определить:
1) индивидуальные и общий индексы физического объема товарооборота;
2) индивидуальные и общий индексы цен;
3) общий индекс товарооборота в действующих ценах.
Решение:
Определение индивидуальных индексов цен определяется по формуле:
Определение индивидуального индекса:
100 + 30 =1,3(А) 100 +60 = 1,6 (Б) 100+40 = 1,4 (В)
100 100 100
Использование формулы средней гармонической при вычислении общего индекса цен:
1460 = 1,45
= 276 + 559 + 625
1,3 1,6 1,4
В общем цены выросли на 45%.
Общий индекс товарооборота в действующих ценах определяется по формуле:
= 1460 / 1170 =1,248
Общий товарооборот вырос на 24,8%.
Используя систему взаимосвязанных индексов товарооборота:
 |  |  |
= ×
|
|
На основе этой системы по двум известным индексам определяется значение третьего неизвестного индекса физического объема товарооборота:
Iq = Ipq/ Ip = 1,25 / 1,45 = 0,86 физический объем снизился на 86% - 100% =14%
Задание 1
На основании данных таблицы 64 определить:
1) индивидуальный и общий индексы цен;
2) общий индекс товарооборота в фактических ценах;
3) индекс покупательной способности тенге;
4) сумму экономического эффекта, полученную в результате изменения цен.
Таблица 64
Изменение товарооборота и цен на товары
|
Наименование товаров | Продажа в фактических ценах, млн. тенге | Изменение цен во II периоде по сравнению с I периодом, % | |
| I период | II период | ||
| ПЭВМ Телефаксы Телефоны | 550 329 251 | 590 465 345 | +60 +45 +70 |
Задание 2
На основании данных таблицы 65 определить:
1) индивидуальные и общие индексы цен;
2) общий индекс товарооборота в фактических ценах;
3) общий индекс физического объема, используя взаимосвязь индексов;
4) абсолютную экономию (перерасход) от изменения цен.
Таблица 65
Товарооборот товаров, млн. тенге
| Товары | Товарооборот за I квартал | Товарооборот II квартал |
| А В С | 68,2 48,0 26,8 | 66 92,5 20,5 |
Во втором квартале по сравнению с первым цены на товар А повысились на 5%, на товар В снизились на 1%, а на товар С остались без изменения.
Задание 3
На основании данных таблицы 66 определить общий индекс цен и физического объёма продукции.
Таблица 66
Цены на овощи
| Продукция | Физический объем, в кг. | Цена за кг, тенге | ||
| Базисный q0 | Отчетный q1 | Базисный p0 | Отчетный p1 | |
| Картофель | 100 | 120 | 60 | 70 |
| Свекла | 80 | 90 | 55 | 60 |
| Итого: | 180 | 210 | ||
Задание 4
На основании данных таблицы 67 определить:
1) общий индекс товарооборота в фактических ценах;
2) индивидуальные и общий индексы цен;
3) индивидуальные и общий индексы физического объема;
4) абсолютные изменения товарооборота в целом и по факторам (влияние цен и влияние физического объема продаж) как по отдельным товарам, так и в целом.
Таблица 67
Товарооборот в фактических ценах, млн. руб.
| Товары | Товарооборот в фактических ценах | Изменения цен в % к базисному периоду | |
| базисный период | отчетный период | ||
| А | 141,5 | 262,6 | +4 |
| Б | 122,5 | 121,0 | – 2 |
| В | 136,0 | 148,8 | без изменений |
Задание 5
На основании данных таблицы 68 определить:
1) индивидуальные индексы физического объема продаж и цен;
2) агрегатный индекс физического объема продаж;
3) агрегатный индекс цен;
4) абсолютную экономию (перерасход) денежных средств покупателей от снижения (повышения) цен на товары.
Таблица 68
Цена и объем продаж товаров
| Наименование | Продано, единиц | Цена единицы, тыс. тенге | ||
| товара | базисный период | отчетный период | базисный период | отчетный период |
| А | 700 | 600 | 10 | 9 |
| В | 210 | 200 | 12 | 15 |
| С | 120 | 150 | 14 | 13 |
Задание 6
На основании данных таблицы 69 определить:
1) общий индекс цен и экономию (перерасход) у населения от изменения цен;
2) общий индекс товарооборота в неизменных ценах и влияние на объем товарооборота изменения физического объема продаж товаров;
3) общее изменение товарооборота в относительных и абсолютных величинах.
Таблица 69
Товарооборот товарных групп, млн. руб.
| Товарные группы | Товарооборот за 3-й квартал | Товарооборот за 4-й квартал | Изменение цен в 4-м кв. по отношению к 3-му, % |
| А | 428,2 | 662,6 | +6,5 |
| Б | 248 | 330 | – 2 |
| В | 326,8 | 430,7 | 0 |
Задание 7
На основании данных таблицы 70 определить:
1) общий индекс цен;
2) общий индекс физического объема товарооборота;
3) индекс цен товарооборота в фактических ценах;
4) абсолютное изменение товарооборота в млн. руб. в целом и по отдельным факторам, сумму перерасхода у населения от роста цен на товары.
Таблица 70
Товарооборот товарных групп
| Товарные группы | Продано товаров в ценах соответствующего периода, млн.руб. | Изменения цен по сравнению с прошлым, % | |
| прошлый год | отчетный год | ||
| А | 633,5 | 685,0 | +15 |
| Б | 845 | 840 | +10,5 |
| В | 521,8 | 724,7 | без изменений |
Задание 8
На основании данных таблицы 71 определить:
1) общий индекс товарооборота в фактических ценах;
2) индивидуальные и общий индексы цен;
3) индивидуальные и общий индексы физического объема;
4) абсолютные изменения товарооборота в целом и по факторам (влияние цен и влияние физического объема продаж) как по отдельным товарам, так и в целом.
Таблица 71
Товарооборот товарных групп
| Товарные группы | Товарооборот в фактических ценах, млн. руб. | Изменения цен в % к базисному периоду | |
| базисный период | отчетный период | ||
| А | 141,5 | 262,6 | +4 |
| Б | 122,5 | 121,0 | – 2 |
| В | 136,0 | 148,8 | без изменений |
Задание 9
На основании данных таблицы 72 определить:
1) средние себестоимости 1 т. молока за 1-й и 2-й кварталы;
2) индекс средней себестоимости;
3) индекс постоянной структуры производства молока;
4) индекс влияния структурных сдвигов;
5) абсолютные изменения средней себестоимости в целом и по отдельным факторам.
Таблица 72
Изменение себестоимости и объема производства молока в двух фермах
| Фермы | Объем производства по кварталам, тонны | Себестоимость 1 т. молока, тыс. руб. | ||
| 1 -й квартал | 2-й квартал | 1-й квартал | 2-й квартал | |
| А | 120 | 150 | 1000 | 1100 |
| Б | 250 | 220 | 1200 | 1300 |
Задание 10
На основании данных таблицы 73 определить:
1) общий индекс товарооборота в неизменных ценах;
2) индивидуальные и общий индексы цен;
3) общий индекс товарооборота в фактических ценах;
4) сумму экономии (перерасхода) у населения от изменения цен;
5) абсолютные размеры изменения объема товарооборота за счет цен, физического объема продаж в целом.
Таблица 73
Товарооборот товарных групп, млн. руб.
| Товарные группы | Товарооборот в фактических ценах | Изменения цен в 3-м квартале по сравнению со 2-м кварталом, % | |
| 2-й квартал | 3-й квартал | ||
| А | 260 | 385 | без изменений |
| Б | 810 | 1235 | +30 |
| В | 120 | 240 | –10 |
Задание 11
На основании данных таблицы 74 определить:
1) индекс средних цен переменного, постоянного состава и структурных изменений;
2) изменение средних цен (в абсолютных величинах) в целом и за счет влияния отдельных факторов.
Таблица 74
Цены и объемы продаж картофеля на трех рынках
| Рынки | 2-й квартал | 3-й квартал | ||
| Количество, ц. | Цена, тенге за 1 кг | Количество, ц | Цена, тенге за 1 кг | |
| 1 | 120,0 | 70 | 180,0 | 75 |
| 2 | 140,0 | 80 | 160,0 | 85 |
| 3 | 140,0 | 90 | 180,0 | 95 |
Задание 12
На основании данных таблицы 75 определить:
1) индивидуальные индексы цен и физического объема реализации;
2) сводные индексы цен, физического объема реализации;
3) индекс товарооборота;
4) сумму дополнительных расходов населения за сч
|
|
|
