Построение экспериментальной переходной функции объекта

Управления

Проведение эксперимента начинают с установки на объекте управления выбранного режима работы, который характеризуется постоянством выходной переменной и всех влияющих на нее переменных. Уста­новившийся режим работы при заранее выбранном значении выходной переменной 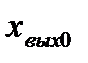выдерживают 2,0—2,5 мин для медленно протекающих процессов, связанных, например, с изменением температуры или влажности, и 0,3—0,5 мин — для более быстро протекающих процессов, таких, например, как изменение давления или расхода.

Затем скачком вводят испытательное воздействие и одновременно начинают регистрировать изменение выходной переменной во времени. Для дальнейшей оценки вида испытатель­ного воздействия необходимо также определить время его внесения. Помимо регистрации выходной переменной в процессе эксперимен­та желательно, если это возможно, записывать изменения основных возмущающих переменных и, в первую очередь, нагрузки объекта.

Окончание переходного процесса определяется по значению выходной переменной. При экспериментальном определении переходной функции на объектах с самовыравниванием (ρ >0) опыт считается законченным, если выходная переменная, начиная с некоторого момента времени, остается практически неизменной, а на объектах без самовыравнивания (ρ = 0)—если скорость изменения переменной достигает своего постоянного максимального значения.

Результаты эксперимента удобно представить в виде таблицы 6.1.

 

Таблица 6.1 – Экспериментальные данные для построения переходного

процесса

№ п/п	время	Значение входного параметра	Значение выходного параметра
	t0	x(t0)	h(t0)
	t1	x(t1)	h(t1)
	t2	x(t2)	h(t2)
…	…	…	…
n	tn	x(tn)	h(tn)

Рассмотрим синтез автоматической системы регулирования технологическим параметром на конкретном примере.

Пример. Экспериментальным путем на реально действующем объекте управления по нормализации молока построить графики переходного процесса.

Для этого на вход подается ступенчатое воздействие x(t) – расход молока от 1,2 до 1,6 кг/м³. Отслеживаются и записываются в таблицу 6.2 значения выходной величины.

Таблица 6.2 – Экспериментальные данные для построения переходной

функции ОУ

t, сек.
x(t), м3/ч	1,2	1,59	1,6	1,6	1,6	1,6	1,6	1,6	1,6	1,6	1,6
y(t), м			2,04	2,09	2,13	2,15	2,17	2,18	2,19	2,2	2,2

На рисунке6.1 представлен график скачкообразного воздействия на объект управления. Для построения графика использована программа MathCad.

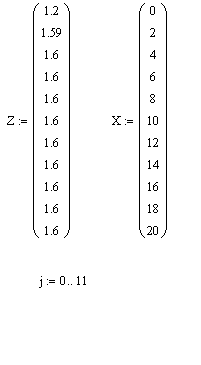
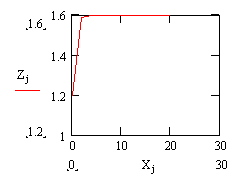
Z_j – изменение входной величины,

X_j – время

Рисунок 6.2 – График скачкообразного изменения входного воздействия

По данным таблицы 6.2 строится экспериментальная переходная функция объекта управления y(t) в программе MathCad.

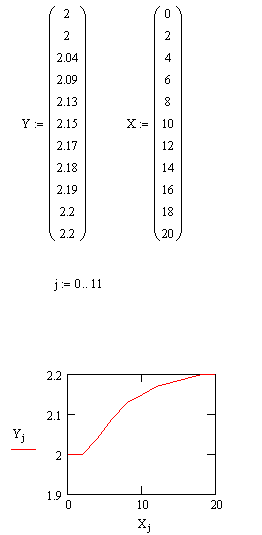
Y_j- изменение выходной величины, м; X_j- время, сек.

Рисунок 6.3 – Переходная функция объекта управления y(t),

 

Определение параметров передаточной функции объекта

Управления

Определение динамических параметров объекта по его экспериментально снятой переходной функции производят графическими или графоаналитическими методами.

В таблицах 6.3 и 6.4 приведены наиболее распространенные ме­тоды определения динамических параметров объекта и показаны графические построения, выполняемые при их использовании.

Таблица 6.3 - Определение динамических параметров объекта с самовыравниванием по экспериментальной переходной функции

 

 

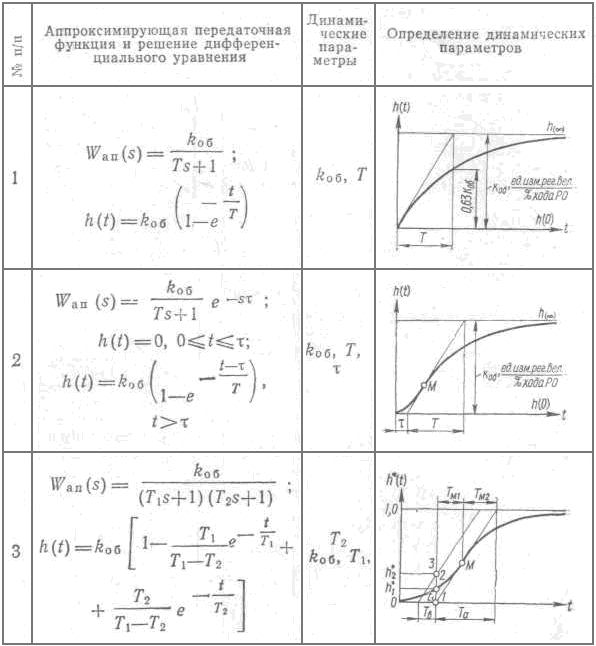
Таблица 6.4- Определение динамических параметров объекта без самовыравнивания по экспериментальной переходной функции

При определении динамических параметров объекта с самовы­равниванием вначале проводят линию нового установившегося значения h (∞), которого переходная функция должна достигнуть за бесконечное время. Её проводят на расстоянии примерно0,05[ h (∞)— h (0)]от последних опытных значений переходной функции. Значение коэффициента передачи объекта определяют как разность установившихся нового и начального значений переход­ной функции:

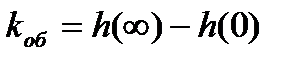(1)

Для определения временных постоянных проводят касатель­ную в точке переходной функции, в которой скорость изменения 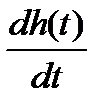имеет максимальное значение, т. е. из всех возможных ка­сательных, которые можно провести к переходной функции, эта касательная должна иметь наибольший угол наклона.Проекция отрезка касательной, заклю­ченного между прямыми h (0) и h (∞), на ось времени равна по­стоянной времени T.

Пример: Вид полученной выше экспериментальной переходной функции позволяет сделать вывод, что с достаточной для практических задач точностью данный объект можно аппроксимировать последовательным соединением следующих типовых динамических звеньев: звеном чистого запаздывания и апериодическим звеном первого порядка. Таким образом, выражение для передаточной функции объекта управления будет иметь вид:

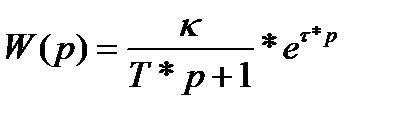, (2)

где К=0,23;

T=9;

τ=2.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: