Охарактеризуйте методы принятия управленческих решений

 

Эффективность управления зависит от комплексного применения многих факторов и не в последнюю очередь - от процедуры принимаемых решений и их практического воплощения в жизнь. Для того, чтобы управленческое решение было действенным и эффективным, нужно соблюсти определенные методологические основы.

Метод - способ, прием выполнения тех или иных действий.

Все методы принятия управленческих решений можно объединить в три группы:

· - неформальные (эвристические);

· - коллективные;

· - количественные.

- Неформальные(основанные на аналитических способностях и опыте руководителя)- совокупность логических приемов и методов выбора оптимальных решений руководителем путем теоретического (мыслительного) сравнения альтернатив с учетом накопительного опыта, базирующихся на интуиции. Преимущество заключается в том, что решения, как правило, принимаются оперативно. Недостаток заключается в том, что данный метод базируются, как правило, на интуиции, а отсюда - довольно высокая вероятность ошибок.

- Коллективные - метод "мозговой атаки", "мозговой штурм" - применяется, как правило, при необходимости принятия экстренного, сложного, многопланового решения, связанного с экстремальной ситуацией. Это требует от руководителей твердого мышления, умения излагать предложение конструктивно, коммуникабельно, компетентно. В ходе "мозговой атаки" предлагаются различные альтернативы, даже такие, которые выходят за рамки обычных приемов и способов реализации подобных ситуаций в обычных условиях.

Метод Делфи (по названию древнегреческого города Дельфы, известного жившими там мудрецами - предсказателями будущего) - многоуровневое анкетирование. Руководитель объявляет проблему и предоставляет подчиненным возможность формулирования альтернатив. Первый этап формулирования альтернатив проходит без аргументации, т.е. каждым из участников предлагается набор решений. После оценки эксперты предлагают подчиненным рассмотреть данный набор альтернатив.

На втором этапе сотрудники должны аргументировать свои предложения, варианты решения. После стабилизации оценок опрос прекращается и принимается предложенное экспертами или скорректированное наиболее оптимальное решение.

Метод "кингисе" - японская кольцевая система принятия решения, суть которой в том, что на рассмотрение готовится проект новации. Он передается для обсуждения лицам по списку, составленному руководителем. Каждый должен рассмотреть предлагаемый проект и дать свои замечания в письменном виде, после чего проводится совещание, на которое приглашаются сотрудники, чье мнение не совсем понятно, либо выходит за рамки обычного решения.

Решения принимаются руководителем на основе экспертных оценок с помощью одного из следующих принципов:

· - принципа большинства голосов;

· - принципа диктатора - за основу берется мнение одного лица группы;

· - принципа Курно - каждый эксперт предлагает свое решение; выбор не должен ущемлять интересов каждого в отдельности;

 

· - принципа Парето - эксперты образуют единое целое, одну коалицию;

 

· - принципа Эджворта - эксперты разбились на несколько групп, каждой из которых невыгодно отменять свое решение. Зная предпочтения коалиций, можно принять оптимальное решение, не нанося ущерба друг другу.

- Количественные - в их основе лежит научно-практический подход, предполагающий выбор оптимальных решений путем обработки больших массивов информации.

В зависимости от типа математических функций, лежащих в основе моделей, различают:

· - линейное моделирование (используются линейные зависимости);

· - динамическое программирование (позволяет вводить дополнительные переменные в процессе решения задач);

· - вероятностные и статистические модели (реализуются в методах теории массового обслуживания);

· - теорию игр (моделирование таких ситуаций, принятия решения в которых должно учитывать несовпадение интересов различных подразделений);

· - имитационные модели (позволяют экспериментально проверить реализацию решений, изменить исходные предпосылки

 

 

11. Какие классификационные группы экономико-математических моделей Вы знаете?

В экономико-математическом моделировании модели разделяются на классы по ряду признаков, относящихся к особенностям моделируемых объектов, целям моделирования и используемого инструментария.

Макроэкономические модели описывают экономику как единое целое со связями между агрегированными материальными и финансовыми показателями (ВВП, потребление, инвестиции, занятость, денежная масса, государственный долг, инфляция и др.).

Микроэкономические модели описывают взаимодействия структурных и функциональных составляющих экономики либо их поведение в отдельности в рыночной среде.

Теоретические модели являются аппаратом изучения общих свойств экономики и ее составляющих на основе дедукции выводов из формальных предпосылок.

Прикладные модели представляют собой аппарат оценок параметров конкретных экономических объектов, выработки рекомендаций для принятий экономических решений и разработки стратегии поведения фирм на рынке.

Равновесные модели описывают такие состояния экономики, когда результирующая всей воздействий на нее равна нулю. Как правило, равновесные модели являются описательными.

Оптимизационные модели используются в теории рыночной экономики на микроуровне (оптимизация деятельности потребителя, производителя или фирмы). На макроуровне результат выбора экономическими субъектами рационального поведения может приводить к состоянию относительного равновесия.

Статические модели описываю состояние экономических объектов в определенный момент или усреднено за некоторый период времени. При этом все параметры статических моделей полагаются фиксированными величинами, не зависящими от времени.

Динамические модели включают в себя зависимость и взаимосвязи переменным модели во времени. Они используют обычно аппарат дифференциальных и разностных уравнений и вариационного исчисления, где независимой переменной является время.

Детерминированные модели предполагают в своей основе только жесткие функциональные связи между переменными модели.

Стохастические модели допускают наличие случайных связей между переменными модели. Эти модели используют аппарат теории вероятностей и математической статистики.

Модели с элементами неопределенности используются для моделирования ситуаций, когда для определяющих факторов невозможно собрать статистические данные, и их значения неопределенны. В этих моделях используется аппарат теории игр и имитационного моделирования.

Экспортные модели – разрабатываются и имеют применение в ряде исследований экономических процессов, когда в условиях отсутствия количественных характеристик за основу принимаются мнения экспертов с оценками разных аспектов по определенной шкале. Эти оценки могут быть использованы в виде векторов некоторой размерности, которые, в свою очередь, можно сравнивать по мере их близости.

Предназначение модели состоит в том, что она является инструментом обработки информации.

 

 

12. Какие классификации решаемых экономических задач можно выделить?

По уровню информации о ситуации:

1. Детерминированный уровень – наиболее простой уровень информации о ситуации- когда условие, в которых принимаются решения, известны полностью.

2. Стохастический уровень – уровень, при котором известно множество возможных вариантов условий и их вероятностное распределение.

3. Неопределенный уровень - уровень, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях.

По виду информации о ситуации:

1. Статический вид – информация о ситуации не меняется во времени и известна заранее.

2. Динамический вид – информация о ситуации зависит от времени, прошедшего от начала операции.

По виду критерия оптимальности:

1.Однокритериальные задачи

2.Монокритериальные задачи

 

По типу критерия оптимальности:

1.Линейные задачи

2.Нелинейные задачи

 

По типу области ограничения:

1.Выпуклая область

2.Целочисленная область

3.Булева область

 

13. Поясните Основные понятия, используемые при решении задач оптимизации

Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели.

 

Цель оптимизации - предварительное количественное обоснование оптимальных решений.

 

Решение - Всякий определенный выбор зависящих от нас параметров.

 

Оптимальным называется решение, по тем или другим признакам предпочтительнее перед другими.

Элементы решения - параметры, совокупность которых образует решение.

Множеством допустимых решений называются заданные условия, которые фиксированы и не могут быть нарушены.

 

Показатель эффективности- количественная мера, позволяющая сравнивать по эффективности разные решения.

Все решения принимаются всегда на основе информации, которой располагает лицо принимающее решение (ЛПР).

Каждая задача в своей постановке должна отражать структуру и динамику знаний ЛПР о множестве допустимых решений и о показателе эффективности.

 

Задача называется статической, если принятие решения происходит в наперед известном и не изменяющемся информационном состоянии.

Задача называется динамической - если информационные состояния в ходе принятия решения сменяют друг.

Информационные состояния ЛПР могут по-разному характеризовать его физическое состояние:

-Если информационное состояние состоит из единственного физического состояния, то задача называется определенной.

-Если информационное состояние содержит несколько физических состояний и ЛПР кроме их множества знает еще и вероятности каждого из этих физических состояний, то задача называется стохастической (частично неопределенной).

-Если информационное состояние содержит несколько физических состояний, но ЛПР кроме их множества ничего не знает о вероятности каждого из этих физическихсостояний, то задача называется неопределенной.

 

14. Перечислите основные виды задач линейного программирования

Линейное программирование – метод решения задач оптимизации.

В отдельных оптимизационных задачах требуется выяснить, сколько различных изделий нужно произвести, чтобы получить максимальный доход, если известно количество ресурсов (сырья, рабочего времени, оборудования) и цены, по которым можно реализовать готовые изделия. Другой вид задач – выяснить, при каких условиях свести расходы к минимуму (это, например, задача о питании). Третий вид задач – оптимизировать транспортные перевозки, т.е. составить план перевозок так, чтобы стоимость всех перевозок была наименьшей.

Таким образом, общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений.

При этом переменные должны принимать неотрицательные значения (то есть положительные либо нулевые).

Функция цели в задаче линейного программирования обычно записывается так:

.

Или в сокращённом виде:

.

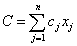Можно встретить обозначение целевой функции и через C, и через F.

Система ограничений в задаче линейного программирования обычно записывается так:

.

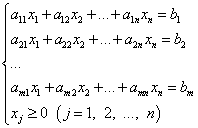Или в сокращённом виде:

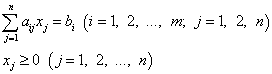
И система ограничений, и целевая функция имеют линейный характер, то есть содержат переменные только в первой степени.

Канонической задачей линейного программирования называется задача, в которой требуется найти максимум целевой функции при ограничениях, заданных системой линейных уравнений. Если все или некоторые ограничения в системе заданы неравенствами, то задачу можно свести к канонической путём преобразования неравенств в уравнения.

Множество чисел (запись последовательности иксов), удовлетворяющих системе ограничений, называется решением этой системы. Решение системы также часто называется планом, и немного реже – программой, но именно отсюда и пошло название «линейное программирование».

Оптимальным решением задачи линейного программирования называется решение системы, при которых функция цели обращается в максимум или минимум, в зависимости от условия задачи, или в общем смысле – в оптимум.

Задачи, решаемые методами ЛП, очень разнообразны по содержанию. Но их математические модели схожи и условно объединяются в три большие группы задач:

• транспортные задачи;
• задачи о составлении плана;
• задачи о смеси (о диете).

Рассмотрим примеры конкретных экономических задач каждого типа, подробно остановимся на построении модели каждой задачи.

Транспортная задача

На двух торговых базах А и В имеется 30 гарнитуров мебели, по 15 на каждой. Всю мебель требуется доставить в два мебельных магазина, С и Д причем в С надо доставить 10 гарнитуров, а в Д - 20. Известно, что доставка одного гарнитура с базы А в магазин С обходится в одну денежную единицу, в магазин Д - в три денежных единицы. Соответственно с базы В в магазины С и Д: две и пять денежных единиц. Составить план перевозок так, чтобы стоимость всех перевозок была наименьшей.
Данные задачи для удобства разметим в таблице. На пересечении строк и столбцов стоят числа, характеризующие стоимость соответствующих перевозок (табл. 1).

Таблица 1

магазины / базы	С	Д	отправлено гарнитуров
А
В
получено гарнитуров			30 = 30

Составим математическую модель задачи.
Необходимо ввести переменные. В формулировке вопроса говорится, что необходимо составить план перевозок. Обозначим через х ₁, х ₂ количество гарнитуров, перевозимых с базы А в магазины С и Д соответственно, а через у ₁, у ₂ - количество гарнитуров, перевозимых с базы В в магазины С и Д соответственно. Тогда количество мебели, вывозимое со склада А, равно (х ₁ + х ₂), а со склада В - (у ₁ + у ₂). Потребность магазина С равна 10 гарнитурам, и в него привезли (х ₁ + у ₁) штук, т. е. х ₁ + у ₁ = 10. Аналогично, для магазина Д имеем х ₂ + у ₂ = 20. Заметим, что потребности магазинов в точности равны количеству гарнитуров, имеющихся на складах, поэтому х ₁ + у ₂ = 15 и у ₁ + у ₂ = 15. Если бы со складов вы увезли меньше, чем по 15 комплектов, то магазинам не хватило бы мебели для удовлетворения их потребностей.
Итак, переменные х ₁, х ₂, у ₁, у ₂ по смыслу задачи неотрицательны и удовлетворяют системе ограничений:
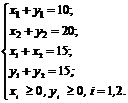(3.1)
Обозначив через F транспортные расходы, посчитаем их. на перевозку одного комплекта мебели из А в С тратится одна ден. ед., на перевозку x ₁ комплектов - x ₁ ден. ед. Аналогично, на перевозку x ₂ комплектов из А в Д затратится 3 x ₂ ден. ед.; из В в С - 2 y ₁ ден. ед., из В в Д - 5 y ₂ ден. ед.
Итак,
F = 1 x ₁ + 3 x ₂ + 2 y ₁ + 5 y ₂ → min (3.2)
(мы хотим, чтобы общая стоимость перевозок была минимальной).
Сформулируем задачу математически.
На множестве решений системы ограничений (3.1) найти такое решение, которое обращает в минимум целевую функцию F (3.2), или найти оптимальный план (x ₁, x _2, y ₁, y ₂), определяемый системой ограничений (3.1) и целевой функцией (3.2).
Задача, которую мы рассмотрели может быть представлена в более общем виде, с любым числом поставщиков и потребителей.
В рассмотренной нами задаче наличие груза у поставщиков (15 + 15) равно общей потребности потребителей (10 + 20). Такая модель называется закрытой, а соответствующая задача - сбалансированной транспортной задачей.
В экономических расчетах немалую роль играют и так называемые открытые модели, в которых указанное равенство не соблюдается. Либо запас у поставщиков больше потребности у потребителей, либо спрос превышает наличие товара. заметим, что тогда в систему ограничений несбалансированной транспортной задачи наряду с уравнениями будут входить и неравенства.

Рассмотрим пример несбалансированной транспортной задачи.
В пунктах А и В расположены кирпичные заводы, а в С и Д - карьеры, снабжающие их песком. потребность заводов в песке меньше, чем производительность карьеров. Известно, сколько песка нужно каждому из заводов и сколько добывается в каждом карьере. Также известна стоимость перевозки 1 т песка из каждого карьера к заводам (числа на стрелочках). Нужно так спланировать снабжение заводов песком, чтобы затраты на перевозку были наименьшими. Данные задачи на схеме.

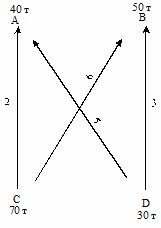
Постоим математическую модель задачи.
Введем переменные:
x ₁₁ - количество тонн песка, перевозимого с карьера С на завод А;
x ₁₂ - с карьера С на завод А;
x ₂₁ - количество тонн песка в А с карьера Д;
x ₂₂ - количество тонн песка с карьера Д на завод В.
На завод А должно быть доставлено 40 т с обоих карьеров, значит x ₁₁ + x ₂₁ = 40, на завод В должно быть доставлено 50 т, значит x ₁₂ + x ₂₂ = 50. Из карьера С вывезено не более 70 т, т. е. x ₁₁ + x ₁₂ ≤ 70, аналогично x ₂₁ + x ₂₂ ≤ 30. Имеем систему ограничений:
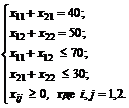(3.3)
И целевая функция F, выражающая стоимость перевозок, имеет вид
F = 2 x ₁₁ + 6 x ₁₂ + 5 x ₂₁ + 3 x ₂₂→min. (3.4)

Задача о составлении плана

Некоторому заводу требуется составить оптимальный план выпуска двух видов изделий, которые обрабатываются на четырех видах машин. Известны определенные возможности и производительность оборудования; цена изделий, обеспечивающая прибыль заводу, составляет 4 тыс. руб. за изделие I вида, 6 тыс. руб. - за изделие II вида. Составить план выпуска этих изделий так, чтобы от реализации их завод получил наибольшую прибыль. В таблице указано время, необходимое для обработки каждого из двух видов изделий на оборудовании всех четырех видов (табл. 3.2).

Таблица 3.2

Изделия	Виды машин
I		0,5
II
Возможное время работы машин

Построим математическую модель.
В задаче необходимо определить план выпуска изделий, обозначим за x количество изделий I вида, за y - количество изделий II вида. Тогда посчитаем, сколько времени затратит первая машина на обработку всех производственных изделий. Она тратит одну единицу времени на одного изделие I вида, значит на x штук изделий потратит 1 x ед. времени, на обработку y изделий II вида затратится 1 y ед. времени. Всего резерв времени работы первой машины - 18 единиц времени. Значит, x + y ≤ 18. Аналогичные рассуждения со второй машиной, третьей и четвертой дадут систему ограничений:
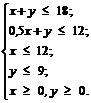(3.5)
Общая прибыль будет выражена в целевой функции:
F = 4 x + 6 y → max. (3.6)
Задача состоит в нахождении на множестве решений системы (3.5) такого решения, при котором значение целевой функции (3.6) было бы максимальным.

Задача составления смеси

Еще одна распространенная задача ЛП - задача о составлении смеси. Примером таких задач может быть задача о составлении таких смесей нефтепродуктов, которые бы удовлетворяли определенным техническим требованиям и были наиболее дешевыми по стоимости. Либо задачи о рационе, когда известна потребность в определенных веществах и содержание этих веществ в различных продуктах. Необходимо составить рацион так, чтобы удовлетворить потребности в необходимых веществах и при этом продуктовая корзина имела бы минимальную стоимость при заданных ценах на продукты.
Практически подобные задачи ставятся, к примеру, в любом животноводческом хозяйстве и имеют очень большой спектр применения.
Рассмотрим пример. Для откорма цыплят на птицефабрике в их рацион необходимо включать не менее 33 единиц вещества А, 23 единиц питательного вещества В, 12 единиц С. Для откорма используются три вида корма. Данные о содержании питательных веществ в каждом виде корма заданы таблицей. Также известна стоимость кормов. Необходимо составить наиболее дешевый рацион (табл. 3.3).

Таблица 3.3

Корма-продукты	Вещества	Стоимость 1 ед. корма
А	В	С
I
II
III

Для понимания задачи можете представить себе, что вещества А, В, С - это жиры, белки, углеводы, а продукты I, II, III - то, чем кормят цыплят, например пшено, комбикорм, витаминные добавки. Тогда первая строка таблицы показывает содержание в одной единице пшена: 4 ед. белка, 3 ед. жиров, одной ед. углеводов. Вторая строка - содержание белков, жиров, углеводов в 1 ед. II продукта и т. д.
Если постановка задачи ясна, приступим к построению математической модели.
В качестве ответа на поставленную задачу мы должны предложить рацион, т. е. указать сколько и каких кормов взять, чтобы необходимое количество питательных веществ было соблюдено и при этом он стоил как можно дешевле.
Поэтому, обозначим за x ₁ количество кормов типа I в рационе, за x ₂ - количество кормов типа II и, соответственно, x ₃ - количество корма III в рационе. Тогда, вещества А при употреблении такого рациона цыплята получат 4 x ₁ - при потреблении продуктов типа I, 3 x ₂ - при потреблении II продукта, 2 x ₃ - при потреблении III. Всего вещества А необходимо употребить по условию задачи не менее 33 единиц, следовательно 4 x ₁ + 3 x ₂ + 2 x ₃ ≥ 33.
Аналогично рассуждая с веществами В и С, имеем:
3 x ₁ + 2 x ₂ + 1 x ₃ ≥ 23 и x ₁ + x ₂ + 2 x ₃ ≥ 12.
Таким образом, получим систему ограничений:
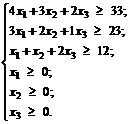(3.7)
Переменные неотрицательны по смыслу задачи. При этом стоимость рациона выражается функцией:
F = 20 x ₁ + 20 x ₂ + 10 x ₃ → min, (3.8)
т. к. 20, 20, 10 - стоимость одной ед. продуктов I, II, III типов соответственно, а в рационе их содержится x ₁, x ₂, x ₃ единиц.
Система ограничений (3.7) вместе с целевой функцией (3.8) и составляют математическую модель исходной задачи. Решить ее - значит найти x ₁, x ₂, x ₃, удовлетворяющие системе ограничений и обращающие значение функции F в минимальное.

 

20. Поясните основные понятия динамического программирования

Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги).

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.

Экономический процесс является управляемым, если можно влиять на ход его развития.

 

Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.

 

Операция – управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.

 

Решение на каждом шаге называется «шаговым управлением».

 

Совокупность всех шаговых управлений представляет собой управление операцией в целом.

При распределении средств между предприятиями шагами целесообразно считать номер очередного предприятия; при распределении на несколько лет ресурсов деятельности предприятия – временной период. В других задачах разделение на шаги вводится искусственно.

 

Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:

F(x)=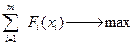

Где F – выигрыш за операцию;

F_i(x_i) – выигрыш на i-м шаге;

х – управление операцией в целом;

х_i – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х₁, х₂, … х_m) могут стать числами, векторами, функциями.

 

То управление (х*), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*₁, х*₂, … х*_m

F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.

Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.

 

 

21. В чем заключается принцип оптимальности Беллмана?

Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.

Суть принципа:

Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться ОПТИМАЛЬНЫМИ относительно состояния, к которому придет система в конце каждого шага.

Важно понимать, что в ДП речь не идет о простой оптимизации каждого шага управления независимо от других шагов. Шаговое управление должно проводиться дальновидно, с учетом последствий в будущем. Т.е. управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах, включая данный.

Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.

Условная оптимизация

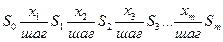
Безусловная оптимизация

S_i – состояние системы на i-м шаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:

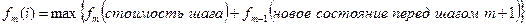, где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге m находится в состоянии i.

Величина f_m(i) – есть максимальная прибыль завершения задачи из состояния i, если предположить, что на шаге m, система находится в состоянии i.

Максимальная прибыль может быть получена максимизацией суммы прибылей самого шага m и максимальной прибыли шага (m+1) и далее, чтобы дойти до конца задачи.

Планируя многошаговую операцию надо выбирать управление на каждом шаге с учетом всех его будущих последствий на ещё предстоящих шагах.

Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы была максимальна сумма выигрышей на всех оставшихся шагах плюс данный шаг.

Среди всех шагов последний шаг планируется без оглядки на будущее, т.е. чтобы он сам, как таковой принес наибольшую выгоду.

Задача динамического программирования начинает решаться с конца, т.е. с последнего шага. Решается задача в 2 этапа:

 

1 этап (от конца к началу по шагам): Проводится условная оптимизация, в результате чего находится условные оптимальные управления и условные оптимальные выигрыши по всем шагам процесса.

 

2 этап (от начала к концу по шагам): Выбираются (прочитываются) уже готовые рекомендации от 1-го шага до последнего и находится безусловное оптимальное управление х*, равный х*₁, х*₂, …, х*_m.

 

24. Каков алгоритм решения задачи распределения средств между двумя предприятиями на 4 года методом динамического программирования?

Для двух предприятий выделено 1400 единиц денежных средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от х единиц, вложенных в первое предприятие равен 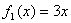, а доход от у единиц, вложенных во второе предприятие равен 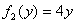. Остаток средств к концу года составляет - для первого предприятия, 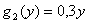- для второго предприятия. Решить задачу методом динамического программирования.

Решение

Процесс распределения средств разобъем на 4 этапа – по соответствующим годам.
Обозначим - средства, которые распределяются на к –ом шаге как сумма средств по предприятиям.

Суммарный доход от обоих предприятий на к –ом шаге:

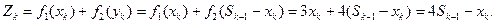
Остаток средств от обоих предприятий на к –ом шаге:

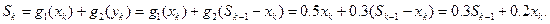
Обозначим - максимальный доход, полученный от распределения средств 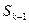между двумя предприятиями с к -го шага до конца рассматриваемого периода.
Рекуррентные соотношения Беллмана для этих функций

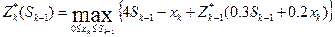- максимум от ф-ии дохода тек периода + ф-ии дохода след периода (к-го + (к+1)-го) -

Проведем оптимизацию, начиная с четвертого шага:

4-й шаг.
Оптимальный доход равен: , т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при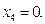

Й шаг.

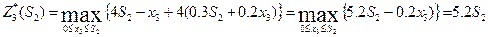
т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при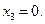

Й шаг.

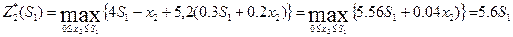
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .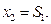

Й шаг.

т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .

Результаты оптимизации:

 

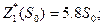
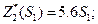
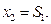
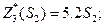
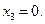
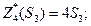
Определим количественное распределение средств по годам:

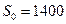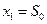Т.к. и , то .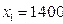

Получаем

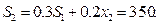
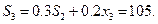
Представим распределение средств в виде таблицы:

предприятие	год

При таком распределении средств за 4 года будет получен доход, равный

 

25. Поясните основные понятия теории игр.

Теория игр - это математическая теория, исследующая конфликтные ситуации, в которых принятие решений зависит от нескольких участников.

Математическая модель конфликтной ситуации называется игрой. Стороны, участвующие в конфликте - игроки, а исход конфликта - выигрыш (проигрыш). Выигрыш или проигрыш может быть задан количественно.

Игра называется антагонистической или игрой с нулевой суммой, если выигрыш одного из игроков равен проигрышу другого, поэтому для полного «задания» игры достаточно указать величину выигрыша первого игрока.

Стратегией игрока называется совокупность принципов, определяющих выбор его действий при каждом личном ходе в зависимости от сложившейся ситуации.

Для того чтобы найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй игрок придерживается своей стратегии. В тоже время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии.

Такие стратегии называются оптимальными.

При выборе оптимальной стратегии следует полагать, что оба игрока ведут себя разумно с точки зрения своих интересов.

Матрица, элементы которой характеризуют выигрыш первого игрока (МЫ –игрок А) и проигрыш второго (игрок В) при их возможных стратегиях (обозначается |α_ij|), называется платежной матрицей игры.

Величина α = max min a_ij называется нижней ценой игры –

j i

гарантированный выигрыш игрока А при применении игроком В своих стратегий. Находится путем выбора минимального значения из a_ij в каждой строке платежной матрицы игры (получаем столбец) и из этих минимальных значений находится максимальное, которое и соответствует нижней цене игры α.

 

Величина β = min max a_ij называется верхней ценой игры –

i j

минимальный проигрыш игрока В при применении игроком А своих стратегий. Находится путем выбора максимального значения из a_ij по столбцам (получим строку) и из этих максимальных значений находится минимальное значение, которое и соответствует верхней цене игры β.

 

Выигрыш, соответствующий оптимальному решению, называется ценой игры γ. Цена игры удовлетворяет неравенству α ≤ γ ≥ β.Такие игры называются играми в смешанных стратегиях.

Если нижняя и верхняя цены игра совпадают, то их общее значение

α = β = γ чистой ценой игры или седловой точкой. Такие игры называются играми в чистых стратегиях.

Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность (А_iВ_j) – оптимальным решением или решением игры.

Игра, в которой интересы игроков противоположны называется антагонистичной.

 

В некоторы

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: