 |
Проецирование прямых частного положения
|
|
|
|
Кроме рассмотренного общего случая, существуют частные случаи расположения прямой по отношению к плоскостям проецирования.
Прямые частного положения имеют важное значение. Необходимо усвоить положение проекций этих прямых на эпюре и уметь безошибочно определять положение таких прямых в пространстве.
Прямые уровня. Прямая, параллельная какой-либо из плоскостей проекций, называется прямой уровня.
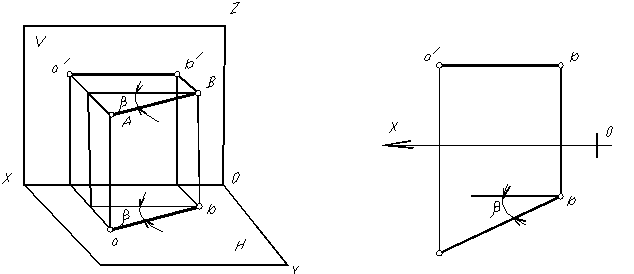 |
Рис. 1.20
Прямая, параллельная горизонтальной плоскости проекций (точки A и В удалены от горизонтальной плоскости проекций на одинаковое расстояние, т.е. ZA = ZB) называется прямой горизонтального уровня или горизонталью (рис. 1.20). Прямая, параллельная фронтальной плоскости (YA = YB) – называется прямой фронтального уровня или фронталью (рис. 1.21).

Прямая, параллельная профильной плоскости (XA = XB) – профильная прямая.
Рис. 1.21
На комплексных чертежах данных прямых уровня, видны углы наклона прямых к плоскостям проекций.
a - угол наклона прямой к горизонтальной плоскости,
b - угол наклона прямой к фронтальной плоскости.
Если прямая параллельна плоскости, то на эту плоскость она проецируется без искажения, т.е своей натуральной величиной. Горизонтальная проекция горизонтали равна длине самой горизонтали, ее фронтальная проекция параллельна оси ОХ. Длина фронтальной проекции фронтали равна длине самой фронтали, ее горизонтальная проекция параллельна оси ОХ.
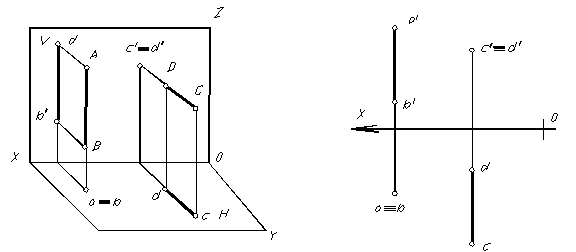 |
Прямые перпендикулярные плоскости
Рис. 1.22
Прямая, перпендикулярная плоскости проекций называется проецирующей прямымой (рис. 1.22). АВ – горизонтально-проецирующая прямая. На горизонтальную плоскость проекций такая прямая проецируется в точку, на фронтальную – в саму себя перпендикулярно оси ОХ. CD – фронтально-проецирующая прямая, На фронтальную плоскость проекций она проецируется в точку, на горизонтальную в саму себя перпендикулярно оси ОХ (рис. 1.22).
|
|
|
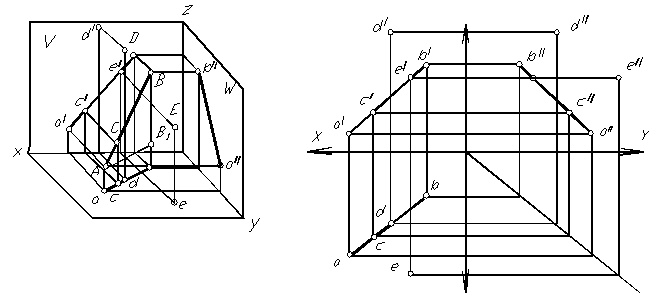
Рис.1.23
Взаимное положение точки и прямой
Если точка принадлежит прямой, то ее проекции принадлежат соответствующим проекциям данной прямой и лежат на одном перпендикуляре к оси. На рисунке 1.15 точка В принадлежит прямой АС, на рисунках 1.16 и 1.17точки А и В принадлежат прямой MN.
На комплексном чертеже (рис. 1.23) показана точка С, принадлежащая прямой АВ, точка D, находящаяся над прямой, E - перед прямой.
Взаимное положение прямых
Прямые в пространстве могут быть параллельны, пересекаться и скрещиваться.
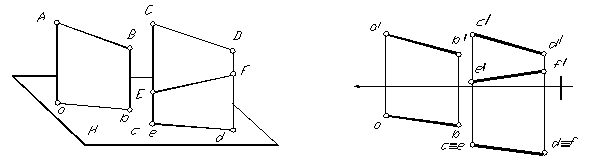 |
Рис. 1.24
Параллельные прямые. Исходя из одного из инвариантных свойств ортогонального проецирования: их одноименные проекции параллельны между собой. если прямая АВ параллельна прямой CD, то, образуя вместе со своими проекциями плоскости перпендикулярные горизонтальной плоскости проекций, они дадут ав параллельно сd (рис. 1.24)
Однако и прямая EF (не параллельная AB) также имеет своей проекцией ef совпадающей с cd. Следовательно, чтобы судить о параллельности прямых в пространстве необходимым должна быть параллельность их горизонтальных, фронтальных, а в некоторых случаях и профильных проекций между собой.

Рис. 1.25 1.26
Справедливо ли обратное заключение, т.е. будут ли параллельны две прямые в пространстве, если на комплексном чертеже их одноименные проекции параллельны? Да, если параллельность одноименных проекций соблюдается на трех плоскостях проекций.
Прямые АВ и CD параллельны, следовательно ab 11 cd. Прямая EF также имеет соей проекцией cd, т.е ab 11 ef, однако АВ не параллельна EF. Следовательно, чтобы судить о параллельности прямых в пространстве по проекциям на одну плоскость не достаточно.
|
|
|
Т.о. заключение о параллельности прямых в пространстве можно сделать по двум проекциям для прямых общего положения.. Если параллельные прямые в свою очередь параллельны какой-либо из плоскостей проекций, то
судить о их параллельности между собой можно лишь имея три проекции данных прямых (рис. 26, 27) или по чередованию буквенных обозначений.
На комплексном чертеже (рис. 1.26) можно сразу установить, что профильные прямые АВ и CD не параллельны между собой, не прибегая к построению третьей проекции, достаточно обратить внимание на чередование буквенных обозначений.

Если через данную точку А требуется провести прямую, параллельную данной CD, то достаточно через горизонтальную проекцию точки А провести прямую параллельную cd, а через а – параллельную cd.
Рис. 1.27 Рис. 1.28
На рисунке 1.27 дан комплексный чертеж параллельных прямых, лежащих друг над другом (прямые принадлежат одной плоскости, которая перпендикулярна горизонтальной плоскости проекций). На рисунке 1.28 - параллельных прямых, лежащих друг перед другом (прямые также принадлежат одной плоскости, перпендикулярной фронтальной плоскости проекций).
Параллельные прямые лежат в одной плоскости.
Пересекающиеся прямые. Если прямые пересекаются, то они имеют одну общую точку (рис.1.29 а).
Исходя из одного из инвариантных свойств ортогонального проецирования, если прямые в пространстве пересекаются, то их проекции пересекаются в точках, лежащих на одном перпендикуляре к оси (на одной проекционной линии связи их разделяющей). Это положение, безусловно только для
 |
а б
Рис. 1.29
прямых общего положения.
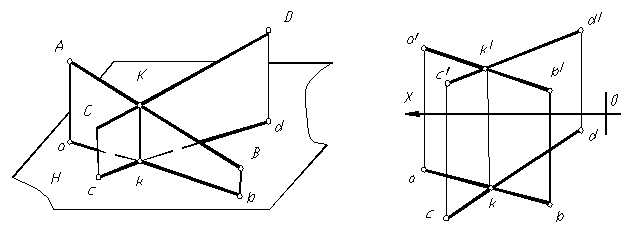
Т.к. прямые пересекаются, то точка К – общая для двух прямых, а исходя из свойства принадлежности точки прямой, проекции точки должны лежать на одном перпендикуляре к оси.
Рис. 1.30 Рис. 1.31
Судить о пересечении прямых в пространстве можно по двум проекциям в том случае, если обе прямые общего положения. Если одна из прямых находится в частном положении (параллельна какой-либо плоскости проекций), то судить о их пересечении можно имея третью проекцию или из условия деления отрезка в пропорциональном отношении (рис. 1.29 б). На рисунке 1.29 а a/k/ : k/ b/ = ak: kb – прямые пересекаются.
|
|
|
На рисунке 1.29 б дан комплексный чертеж прямых АВ и CD (АВ параллельна профильной плоскости проекций – профильная прямая) не пересекающихся между собой. Судить о положении данных отрезков прямых, можно построив третью проекцию, а также из условия деления отрезка в пропорциональном отношении. Отношение проекций отрезков на горизонтальной и фронтальных плоскостях не совпадают.
Пересекающиеся прямые, так же как и параллельные лежат в одной плоскости.
Скрещивающиеся прямые. Скрещивающиеся прямые не параллельны и не пересекаются между собой.
Рис. 1.32
 |
Проекции таких прямых могут пересекаться, но точки пересечения проекций не находятся на одном перпендикуляре к оси (рис. 1.32).
Точки пересечения проекций у скрещивающихся прямых называются конкурирующими. В действительности конкурирующие точки принадлежат разным прямым.
Конкурирующие точки дают возможность судить о положении прямых друг относительно друга в пространстве, а именно используются для определения видимости ребер гранных геометрических тел (призм, пирамид) на отдельных плоскостях проекций. Каждая проекция представляет собой проекции двух точек, из которых одна принадлежит первой прямой, а другая – второй.
Свойства проекций:
а) точки пересечения проекций не лежат на одной линии связи,
б) скрещивающиеся прямые, в отличии от параллельных и пересекающихся не лежат в одной плоскости,
в) через две скрещивающиеся прямые можно провести две параллельные плоскости,
г) расстояние между двумя скрещивающимися прямыми равно расстоянию между проведенными через них параллельными плоскостями.
д) угол между скрещивающимися прямыми равен углу, стороны которого параллельны скрещивающимся прямым.
 |
Определение видимости элементов гранного тела. На рисунке 1.33 с помощью конкурирующих точек определена видимость граней треугольной призмы. Точки 1 и 2, принадлежащие соответственно ребрам AB и SC служат для определения видимости на фронтальной плоскости проекций. Обозначив их на фронтальной проекции ребер, находятся их горизонтальные проекции. Точка 2, принадлежащая ребру AB имеет большую игрековую координату, нежели точка, следовательно, находится ближе к наблюдателю и вместе с ней и ребро AB – ребро AB на фронтальной плоскости видимо. Другая пара конкурирующих точек 3 и 4 служит для определения видимости на горизонтальной плоскости проекций. Точка 4, принадлежащая ребру SC, находится выше точки 3 (у нее больше координата Z чем у точки 3), следовательно ребро SC на горизонтальной плоскости видимо.
|
|
|
|
|
|


