Опорные задачи по теме «Многогранники».

Как уже говорилось, изучение многогранников является важнейшей частью курса стереометрии. Они дают богатый задачный материал как при изучении самой темы «многогранники», так и при изучении последующих тем стереометрии. Чаще всего в учебниках мало простых задач «на геометрические тела», поэтому на уроке удается решить всего 2-3 задачи средней трудности. Но они не всем ученикам под силу. Если ограничиваться только такими задача­ми, то многие ученики не смогут принимать актив­ное участие в их решении, и будут отставать. Если же специально уделять на уроке время для задач, которые сводятся к одной-двум операциям и пото­му доступны для устного решения, то можно втя­нуть в работу всех учеников.

Устное решение задач «на многогранники» зна­чительно улучшает пространственное мышление уча­щихся, которое играет важную роль в стереометрии. Поэтому подробнее остановимся именно на таких задачах.

Так как основные геометрические тела, изучаемые в школе, это призмы и пирамиды, то задачи, приведенные ниже, посвящены темам: «Призма. Пирамида. Их сечения. Площади полной и боковой поверхностей». Кроме того, задачи разбиты на типы: задачи на доказательство, на исследование, на построение, на вычисление.

 Большое количество задач можно предлагать для решения вместе с готовым рисунком, когда один рисунок будет сопровождать несколько задач, в которых идет речь об одном и том же геометрическом теле. Но готовые рисунки сопутствуют далеко не всем задачам, поскольку само изготовление изоб­ражения является важной частью решения. Учитель может варьировать стратегию обучения. В одних случаях - начинать с готового рисунка, а в других ­демонстрировать рисунок (на откидной доске или на экране) только после того, как учащиеся сами сделали нужные изображения в своих тетрадях.

Задачи по теме «Призма».

  Для простоты введем обозначения. Буквами а, b, c обозначим соответственно длину, ширину и высоту прямоугольного параллелепипеда, бук­вой d - длину диагонали основания. Прописные буквы Н, D и P соответствуют высоте, длине наибольшей диагонали призмы и периметру ее ос­нования, а буквы s, Q, S_б и S _n - площадям: s – основания, Q - диагонального сечения, S_б - боко­вой поверхности, S _n - полной поверхности приз­мы. Угол между диагональю прямоугольного парал­лелепипеда и плоскостью основания обозначаем греческой буквой γ.

Задачи на вычисление.

Четырехугольная призма.

Перед решением задач 1 и 2 следует повторить формулы для вычисления элементов куба со сторо­ной a:

, , , .

Задача 3 и некоторые из следующих за ней, в которых речь идет о прямоугольном параллелепипеде, потребуют использования формул:

D² = а² + b ² + с², d ² =a² + b ², s = а b, Q = d ∙ с, S_б= Р ∙с.

1. Ребро куба равно а. Найдите: диагональ гра­ни; диагональ куба; периметр основания; площадь грани; площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трех ребер, выходящих из одной и той же вершины..

2. По рис. 4.1 и по данным элементам в табл. 1 найдите остальные элементы куба.

Таблица 1

а	d	D	s	Q
5
	14
		11
			196

 

3. По рис.4.2 и по данным элементам в табл. 2 найдите остальные элементы прямоугольного па­раллелепипеда.

 

Таблица 2.

а	b	с	d	D	γ	s	Q
3	4	5
5	12
7	24				45˚
8	6
15		17	17

4. Перпендикулярным сечением наклонной 4-угольной призмы является ромб со стороной 3 см. Вычислите площадь боковой поверхности призмы, если боковое ребро равно 12 см.

5. Найдите боковую поверхность наклонного параллелепипеда с боковым ребром 32 см и смеж­ными сторонами перпендикулярного сечения 10 см и 8 см.

6. Сторона основания правильной четырехуголь­ной призмы равна 3 см. Высота призмы - 5 см. Найдите: диагональ основания; диагональ боковой грани; диагональ призмы; площадь основания; площадь диагонального сечения; площадь боковой поверхности; площадь поверхности призмы.

7. Площадь боковой поверхности правильной четырехугольной призмы равна -32 см, а площадь поверхности 40 см. Найдите высоту призмы.

Решение. Площадь основания равна S= (см²), сторона основания - 2 см, периметр основания Р = 8 см, а высота призмы (см²).

 

Треугольная, шестиугольная и n -угольная призмы.

Перед решением задач целесообразно повторить формулы; S_б = РН и   S_п = 2 S_б + 2s для произволь­ной призмы, а также формулы:

Р = 3а, s = 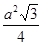 - для правильной треугольной и

Р = 6а, s = 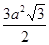 -для правильной шестиуголь­ной призмы со стороной основания а.

8. Расстояния между боковыми ребрами наклон­ной треугольной призмы равны: 2 см, 3 см и 4 см. Боковая поверхность призмы - 45 см'. Найдите ее боковое ребро. ­

Решение. В перпендикулярном сечении призмы - треугольник (рис. 4.3), периметр которого 2 + 3 + 4 = 9 (см), поэтому боковое ребро равно 45: 9 = 5 (см).

9. Вычислите площадь боковой поверхности пра­вильной треугольной призмы, если известно, что площадь сечения, проходящего через средние ли­нии оснований, равна 25 см'.

Решение. В сечении - прямоугольник, у ко­торого одна сторона равна боковому ребру, а дру­гая - половина стороны основания (рис. 4.4). Следо­вательно, его площадь в 2 раза меньше площади бо­ковой грани. Итак, площадь боковой грани 50 см', а боковой поверхности – 50 ∙ 3 = 150 (см').

10. Каждое ребро правильной треугольной приз­мы равно 12 см. Вычислите: площадь основания; площадь боковой поверхности; площадь поверхно­сти; площадь сечения, проведенного через медиану основания и боковое ребро, которые проходят через одну вершину основания.

11. В прямой треугольной призме все ребра рав­ны. Площадь боковой поверхности 12 см'. Найди­те высоту.

12. Найдите неизвестные элементы правильно треугольно   й призмы по элементам, заданным в табл.3.

а	Н	Р	Sб	Sп
6			90
		6
	15		90
		12	144
			108	12б

 

13. Найдите площадь боковой поверхности пра­вильной шестиугольной призмы, если дана площадь Q большего диагонального сечения.

Решение. Площадь большего диагонального сечения (рис. 4.5) Q=2 a H, aH= 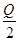. Площадь боковой поверхности равна 6∙ Q = 3 Q.

14. Через две неравные диагонали основания пра­вильной 6-угольной призмы проведены диагональ­ные сечения. Найдите отношение их площадей.

Решение. Отношение площадей диагональных сечений (рис. 4.5-4.6) равно отношению неравных диагоналей правильного 6-угольника, сторона ко­торого а: S₁,: S₂ = 2а: а = 2: .

15. По элементам, данным в табл. 4, найдите неизвестные элементы правильной шестиугольной призмы.

 

 Таблица 4

а	Н	Р	Sб	Sп
4	7
6			720
	5	18
	20		240
		12	144

16. В правильной n-угольной призме проведена плоскость под углом 60˚ к основанию так, что она пересекает все боковые грани призмы. Площадь основания равна 50 см². Найдите площадь сечения.

Решение. S_осн = S_сеч ∙ cos 60,

        S_{се ч} = = 100 (см ²).

17. Дана n-угольная призма. Найти сумму вели­чин ее плоских углов.

Решение. Найдем сумму плоских углов двух оснований и всех боковых граней: 180(n - 2) ∙2 + 360 n = 360 n - 720 + 360 n = 720(n - 1).

 

Задачи на исследование.

1. Поставьте куб так, чтобы ни одна грань не была вертикальной. Будут ли тогда у него горизонталь­ные грани?

                      Ответ: нет.

2. Можно ли куб с ребром в 7 см оклеить лис­том бумаги в виде прямоугольника шириной14 см и длиной в 21 см?

Решение. Для оклейки нужны 6 квадратов со стороной 7 см. Данный прямоугольник разрезать на два со сторонами 7 см и 21 см, а потом каж­дый из них - на три квадрата со стороной 7 см. Получим 6 нужных квадратов, которыми можно оклеить куб.        ­

3. Сколько нужно взять прямоугольников и ка­ким свойством они должны обладать, чтобы из них можно было составить прямоугольный параллеле­пипед?

Решение. Два прямоугольника для оснований со сторонами а и b, четыре прямоугольника для боковой грани. Из них два со сторонами с и а и два со сторонами с и b.

4. Установите, прямой или наклонной является призма, у которой две смежные боковые грани пер­пендикулярны основанию.

Решение. Призма является прямой. Две смеж­ные боковые грани пересекаются по прямой, пер­пендикулярной плоскости основания. Остальные ребра параллельны данному ребру и, следователь­но, тоже перпендикулярны основанию.

5. Исследуйте, существует ли призма, имеющая 50 ребер? 54 ребра?

Решение. Число ребер n-угольной призмы 3 n, поэтому призмы, имеющей 50 ребер, не существу­ет, а 54 ребра имеет 18-угольная призма.

6. Какой многоугольник лежит в основании призмы, если она имеет n граней?

Решение. Число сторон многоугольника, ле­жащего в основании, равно числу боковых граней призмы. Из условия следует, что это число равно n - 2, так как в призме две грани являются основа­ниями. Таким образом, в основании (n - 2)-уголь­ник.

 

Задачи на доказательство.

1. В параллелепипеде диагонали основания рав­ны, а боковое ребро перпендикулярно двум смеж­ным сторонам основания. Докажите, что паралле­лепипед прямоугольный.

Доказательство. В основании - параллелограмм с равными диагоналями, т.е. прямоугольник, а бо­ковое ребро перпендикулярно основанию по при­знаку перпендикулярности прямой и плоскости.

2. Докажите, что число ребер призмы кратно 3.

Доказательство. В n-угольной призме боковых ребер n, а ребер нижнего и верхнего оснований 2 n, всего 3n ребер.

3. Докажите, что сумма двугранных углов при всех боковых ребрах четырехугольной призмы рав­на 360".

Доказательство. Рассмотрим перпендикулярное сечение призмы. В сечении - четырехугольник, сумма его углов S = 180°(4 - 2) = 360°.

4. Если призма имеет 18 граней, то в ее основа­нии лежит 16-угольник. Докажите.

Доказательство. У призмы две грани оснований и, значит, боковых граней 16. Следовательно, в основании 16-угольник.

5. В кубе из вершины N проведены диагонали граней NE, NF, NK Концы их соединены отрез­ками (рис. 4.7). Докажите, что многогранник NEFK­ - правильный тетраэдр.

6. Если две боковые грани треугольной призмы взаимно перпендикулярны, то сумма квадратов их площадей равна квадрату площади третьей боко­вой грани  (рис. 4.8). Докажите.

7. Докажите, что сечение параллелепипеда пло­скостью не может быть правильным пятиугольни­ком.

Доказательство. Среди сторон многоугольника в сечении параллелепипеда плоскостью найдутся параллельные, а у правильного пятиугольника ни­какие две стороны не параллельны.

Задачи на построение

Сечения можно рисовать на заранее подготов­ленном изображении призмы.

1. Постройте сечение куба в виде: а) треугольни­ка, б) четырехугольника, в) пятиугольника, г) ше­стиугольника.

2. Постройте плоскость, проходящую через сто­рону нижнего основания треугольной призмы. Ка­кие многоугольники получаются в сечении приз­мы при вращении этой плоскости вокруг стороны?

Ответ: сечение может иметь форму

       треугольника, трапеции.

3. В правильной треугольной призме плоскость сечения ВСМ образует с плоскостью основания двугранный угол α  (рис. 4.9). Постройте линейный угол этого двугранного угла. Дайте объяснения.

Построение. Проведем из вершины A правиль­ного треугольника АВС высоту АК. Точка K принадлежит ребру ВС. Соответственно отрезок МК перпендикулярен ребру ВС. Угол МКА­ - искомый.

4. В основании прямой призмы (рис. 4.10) лежит равнобедренная трапеция. Сечение ABC ₁ D ₁ обра­зует с плоскостью основания двугранный угол α. Постройте его линейный угол.

Построение. Это угол между высотами трапеций ABCD и ABC ₁ D ₁ проведенными из их общей вер­шины тупого угла. (Используем теорему о трех пер­пендикулярах.)

5. Сечение BCD ₁ A ₁ прямоугольного параллеле­пипеда (рис. 4.11) образует с плоскостью основания двугранный угол β. Как построить его линейный угол?     Построение. Следует использовать теорему о трех перпендикулярах. Искомый угол - это угол между диагональю А₁В (или D ₁ C). боковой грани и стороной основания АВ (или CD), лежащей в этой грани.

 

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: