Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Задачи по теме «Пирамида».

Задачи на вычисление

1. В правильной четырехугольной пирамиде вы­сота составляет с боковой гранью угол, равный 37°. Найдите угол между апофемами противоположных боковых граней.

               Ответ: 74°.

2. Боковое ребро правильной пирамиды вдвое больше ее высоты. Определите угол наклона боко­вого ребра к плоскости основания.

               Ответ: 30°.

3. Периметр основания пирамиды равен 20 см, а площадь ее основания 16 см2. Найдите периметр и площадь сечения пирамиды, проведенного парал­лельно основанию через середину бокового ребра.

   Ответ:10 см, 4 см2.

4. Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника, лежащего в основа­нии, и равны 12 см. Вычислите высоту пирамиды.

         Ответ: 6  см.

5. В правильной четырехугольной пирамиде бо­ковое ребро равно 20 см, оно составляет с основа­нием угол 45°. Определите расстояние от центра основания до бокового ребра.

Решение. Искомое расстояние d равно длине высоты, опущенной из вершины равнобедренного прямоугольного треугольника на гипотенузу, которой является боковое ребро, d = 10 см.

            Ответ: 10 см.

6. Используя рис. 4.12, на котором изображена пра­вильная треугольная пирамида, заполните пустые ячейки в табл. 1 и табл. 2.

      Таблица 1

№ а b h k β
1 6 4      
2 12       45°
3   4     60°
4     4 2  

Таблица 2

 

№ а k h b α
I 2      
2     1   45°
3   4 2    
4 4       60°

Указание. Перед решением задачи следует повто­рить и затем записать на доске формулы

NC = , ON = , OC =

7. Используя рис. 4.13, на котором изображена пра­вильная четырехугольная пирамида, заполните пу­стые ячейки в табл. 3 и табл. 4.

Таблица 3

№ а k h b α
1 2      
2 2       45°
3   6 3    
4   4     30°

Таблица 4

№ а b h k β
1   4     60°
2     2   45°
3   8 4    
4 4 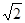8      

Указание. Перед решением этой задачи следует повторить и затем записать на доске формулы

AC = , ON = , OC =

8. Площадь боковой поверхности пирамиды, в основании которой лежит трапеция, равна 2 Q. Бо­ковые грани пирамиды составляют с плоскостью основания равные углы. Найдите сумму площадей боковых граней, проходящих через непараллельные стороны трапеции.

Ответ: Q.

9. В основании пирамиды лежит ромб. Боковые грани пирамиды образуют с основанием равные углы. Площадь одной из боковых граней равна Q. Найдите площадь боковой поверхности пирамиды.

Ответ: 4 Q.

10. Вычислите площадь боковой поверхности правильной пятиугольной пирамиды, если извест­но, что ее боковое ребро. равное а. со стороной основания составляет угол 60°

Ответ: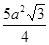

11. Дана правильная треугольная пирамида, у ко­торой а - сторона основания, k - апофема, P - периметр основания, S1 - площадь боковой поверхности, S - площадь пирамиды. Заполните табл. 5.

Таблица 5

№ а k Р S1 S
1 5     75  
2   24 24    
3   18   297  
4     45 315  
5       198 202

Указание. Задачу следует решать по заранее заготовленному чертежу.

Перед решением необходимо повторить и запи­сать на доске формулы:

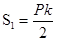, P =3 a, S = S 1 + S 2, S 2 =  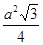 (S2 - площадь основания пирам иды.)

12. Дана правильная четырехугольная пирамида. у которой а - сторона основания, k - апофема, P - периметр основания, S1 - площадь боковой поверхности, S - площадь пирамиды.

 

 

Таблица 6

№ а k р S, S
I 6 12      
2 13       689
3   16   288  
4     44 396  
5       352 416

Указание. Задачу следует решать по заранее заго­товленному чертежу.

Перед решением следует повторить и записать на доске формулы:

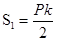, P=4a, S=S1+S2, S2= a2   (S2 - площадь основания пирамиды.)

2)Задачи на исследование.

1. Сколько вершин, ребер и граней имеет n-угольная пирамида?

Ответ:   n + 1 вершин. n + 1 граней, 2п ребер.

2. Какое основание может иметь пирамида, у которой все ребра равны?

Решение. Плоские углы при вершине пира­миды равны 60°, так как каждая боковая грань - ­равносторонний треугольник. Следовательно, бо­ковых граней меньше, чем 360°: 60° = 6. т.е. в основании может быть равносторонний треуголь­ник, квадрат или пятиугольник.

3. В каких пределах находится плоский угол α при вершине правильной n -угольной пирамиды. если n = 3, 4, 5, 6?

4. У треугольной пирамиды все боковые ребра равны. Может ли высота такой пирамиды находить­ся на одной из граней?

Ответ: может, если в основании прямоугольный треугольник.

5. Сравните термины: «правильная треугольная пирамида» и «правильный тетраэдр». Можно ли утверждать, что они определяют одно и то же?

6. Боковые ребра пирамиды равны. Может ли ее основанием быть: а) прямоугольная трапеция, б) ромб?

Ответ: а) не может, поскольку такую тра­пецию нельзя вписать в окружность; б) может только в случае, если осно­вание - квадрат.

7. При каком соотношении в правильной тре­угольной пирамиде между стороной основания а и боковым ребром b ее можно построить?

                   Ответ:   

Задачи на доказательство.

1. Докажите, что число плоских углов в n -уголь­ной пирамиде делится на 4.

2. Если в правильной треугольной пирамиде высота Н равна стороне основания а, то боковые ребра составляют с плоскостью основания углы в 60°. Верно ли это утверждение?

Решение. Высота пирамиды проектируется в центр окружности радиуса R, описанной около основания, α - искомый угол,

tgα =  =  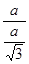= , α=60°.

3. Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правиль­ная».

Решение. Основание пирамиды - правильный многоугольник. Так как боковые ребра равны, то вершина проектируется в центр основания, следо­вательно, пирамида - правильная.

4. Доказать, что сумма площадей проекций бо­ковых граней пирамиды на основание может быть больше площади основания.

Ответ: может, если высота пирамиды не

проходит через основание пирамиды.

5.. Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, пост­роить правильную четырехугольную пирамиду с боковым ребром 7 см.

Решение. Половина диагонали квадрата является катетом в прямоугольном треугольнике, этот катет равен 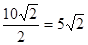,а боковое ребро - гипо­тенуза - равно 7 см. Получается, что катет больше гипотенузы.

6. Доказать, что в правильной пирамиде угол наклона бокового ребра к плоскости основания α меньше угла наклона боковой грани к плоскости основания β.

Задачи на построение.

1. Постройте два изображения одной пирамиды, одно - имеющее наибольшее число видимых ре­бер, другое - наименьшее число видимых ребер.

Указание. Вид со стороны вершины, все ребра видимые. Вид со стороны основания, видны толь­ко ребра основания.

2. В правильной четырехугольной пирамиде (рис. 4.14) апофема образует с плоскостью основания угол 1. Обозначьте этот угол на рисунке.

3. На рис. 4.15 изображена пирамида РАВС, у кото­рой PH  АВС, PK.  ВС, TE РВС, Е PBC. Верен ли чертеж?

Решение. По условию PH АВС, PK ВС, т.е. по теореме о трех перпендикулярах HK  ВС, и PHK PBC. Так как, опять же по условию, TE РВС, то отрезок ТЕ либо параллелен плос­кости РНК, либо принадлежит ей. В любом случае чертеж неверен.

4. На рис. 4.16 изображена пирамида КА BCD. Че­рез точку М, М АВК, провести прямую, парал­лельную BD.

Решение. Проведем через прямую BD и дан­ную точку М плоскость. Она пересечет грань АВК по прямой ВЕ (Е КА), а грань ADK по прямой ED. В построенной плоскости BED проведем через точку М прямую параллельно BD.

5. Постройте точку пересечения прямой МН с плоскостью основания пирамиды SABCD (рис. 4.17).

6. В основании треугольной пирамиды, боковые ребра которой равны, лежит прямоугольный тре­угольник (рис. 4.18). Постройте высоту пирамиды.

7. Через точку М на плоскости α (рис. 4.19) проведена прямая, которая пересекает грань АКС пирамиды КАВС в точке Н. Какую еще грань пересечет эта прямая?

8. Постройте многогранник, имеющий 11 ребер.

Указание. Четырехугольная пирамида имеет 8 ре­бер, если у нее «срезать» угол при основании, добавит­ся 3 ребра. Всего у многогранника будет 11 ребер. [25], [26], [8], [12], [13]

 

 

Заключение

Целью данной работы было рассмотрение особенностей методики изучения темы «Многогранники» в курсе стереометрии 10-11 классов. В связи с чем были выполнены следующие задачи: были рассмотрены различные подходы к определениям многогранника, выпуклого многогранника и правильного многогранника, а также были сделаны выводы о том, какие подходы целесообразнее использовать в школе. Кроме того, были рассмотрены особенности изучения темы в учебниках разной направленности: общеобразовательной, гуманитарной, с математическим уклоном. Были рассмотрены также различные средства наглядности, которые могут быть использованы при изучении данной темы. И, наконец, были подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы.

Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в курсе математики 5-6 классов.


Литература

1. Автономова Т.В. Основные понятия и методы школьного курса геометрии: Книга для учителя./ Т.В. Автономова, Б.И. Аргунов. – М.: Просвещение, 1988.

2. Александров А.Д. Что такое многогранник? / А.Д. Александров// Математика в школе. – 1981. - № 1-2.

3. Александров А.Д. Геометрия для 10-11 классов: Учеб. Пособие для учащихся шк. и классов с углубл. изуч. математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. - М.: Просвещение, 1992. – 464 с.

4. Атанасян Л.С. Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. - М.: Просвещение, 1998. – 207 с.

5. Бескин Л.Н. Стереометрия. / Л.Н. Бескин. - М.: Просвещение, 1971.

6. Болтянский В.Г. Выпуклые многоугольники и многогранники. / В.Г. Болтянский, И.М. Яглом // Математика в школе. – 1966. - № 3.

7. Болтянский В.Г. Элементарная геометрия: Кн. для учителя. / В.Г. Болтянский. - М.: Просвещение, 1985. – 320 с.

8. Веселовский С.Б. Дидактические материалы по геометрии для 11 класса. / С.Б. Веселовский, В.Д. Рябчинская. - М.: Просвещение, 1998. – 96 с.

9. Глаголев Н.А. Геометрия: Стереометрия. / Н.А. Глаголев, А.А. Глаголев. - М.: Учпедгиз, 1958.

10. Джордж Пойа. Математическое открытие. / Джордж Пойа. - М.: Наука, 1976.

11. Земляков А.Н. Геометрия в 10 классе: Метод. рекомендации к преподаванию курса геометрии по учеб. пособию А.В. Погорелова: Пособие для учителя. / А.Н. Земляков. - М.: Просвещение, 1986. – 208 с.

12. Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. - М.: Просвещение, 2000.

13. Зив Б.Г. Задачи к урокам геометрии. 7-11 классы. / Б.Г. Зив. – С.-Петербург, 1998.

14. Каченовский М.И. Математический практикум по моделированию. / М.И. Каченовский. - М.: Просвещение, 1959.

15. Киселев А.П. Геометрия: Учебник для 9-10 классов средней школы. / А.П. Киселев. - М.: Учпедгиз, 1956.

16. Клопский В.М. Геометрия: Учебное пособие для 9 и 10 классов средней школы. / В.М. Клопский, З.А. Скопец, М.И. Ягодовский / Под. ред. З.А. Скопеца. - М.: Просвещение, 1979.

17. Люстерник Л.А. Выпуклые фигуры и многогранники. / Л.А. Люстерник. - М.: Государственное издательство технико-теоретической литературы, 1956.

18. Методика преподавания геометрии в старших классах средней школы. / Под. ред. А.И. Фетисова. - М.: Просвещение, 1967.

19. Методика преподавания математики: Общая методика. / Составители: Р.С. Черкасов, А.А. Столяр. - М.: Просвещение, 1985.

20. Паповский В.М. Углубленное изучение геометрии в 10-11 классах: Метод. рекомендации к преподаванию курса геометрии в 10-11 кл. по учеб. пособию А.Д. Александрова, А.Л. Вернера, В.И. Рыжика: Кн. для учителя. / В.М. Паповский. - М.: Просвещение, 1993. – 223 с.

21. Петрова Е.С. Теория и методика обучения математике: Учеб.-метод. пособие для студ. мат. спец.: В 3 ч. Ч. 1. Общая методика. / Е.С. Петрова - Саратов: Изд-во Сарат. ун-та, 2004. – 84 с.

22. Погорелов А.В. Геометрия: Учеб. для 7-11 кл. сред. шк. / А.В. Погорелов. - М.: Просвещение, 1990. – 384 с.

23. Преподавание геометрии в 9-10 классах. / (сб. статей) сост. З.А. Скопец, Р.А. Хабиб. - М.: Просвещение, 1980.

24. Саакян С.М. Изучение темы «Многогранники» в курсе 10 класса. / С.М. Саакян, В.Ф. Бутузов. // Математика в школе. – 2000. - № 2.

25. Сверчевская И.А. Устные задачи по теме «Призма». / И.А. Сверчевская. // Математика в школе. – 2003. - № 6.

26. Сверчевская И.А. Устные задачи по теме «Пирамида». / И.А. Сверчевская. // Математика в школе. – 2003. - № 7.

27. Смирнова И.М. В мире многогранников: Кн. для учащихся. / И.М. Смирнова. – М.: Просвещение, 1995. – 144 с.

28. Смирнова И.М. Геометрия: Учеб. пособие для 10-11 кл. гуманит. Профиля. / И.М. Смирнова. – М.: Просвещение, 1997. – 159 с.

29. Смирнова И.М. Об определении понятия правильного многогранника. / И.М. Смирнова. // Математика в школе. – 1995. - № 3.

30. Смирнова И.М. Уроки стереометрии в гуманитарных классах. Изучение многогранников. / И.М. Смирнова. // Математика в школе. – 1994. - № 4.

31. Ходеева Т. Свойства многогранников. / Т. Ходеева. // Математика. – 2002. - № 11.


Приложение 1.
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...