Двух- и трехсекторные модели развития национальной экономики

(8 часов)

1) Модель Маркса:

Выполнение работы строится на данных табл.2 (Приложение 3).

Предпосылки модели.

В этой модели выделяются два подразделения общественного производства: I – производство средств производства и II – производство предметов потребления.

Стоимость валового общественного продукта, – как и валового продукта каждого подразделения, – складывается из стоимости постоянного капитала (С), стоимости переменного капитала (V) и прибыли, выражающей прибавочную стоимость (π). Сумма прибыли, образующейся в обоих подразделениях, равняется произведенной прибавочной стоимости (m). Она зависит от нормы прибавочной стоимости, т.е. отношения , которая ежегодно повышается в силу действия объективных законов.

Национальный доход (НД) складывается из вновь созданной стоимости, т.е. стоимости переменного капитала и прибавочной стоимости: V + m = V + π.

Норма прибыли, т.е. отношение прибыли к издержкам производства, или 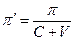– одинаковая в обоих подразделениях.

В каждом подразделении прибыль используется на потребление (П) и накопление (Н), накопление идет на прирост постоянного капитала (ΔС) и переменного капитала (ΔV). Соотношение между ними определяется органическим строением капитала в соответствующем подразделении, т.е. отношением постоянного капитала к переменному: , которое ежегодно возрастает на основе развития технического прогресса.

Связь между подразделениями в каждом году выражается балансовым уравнением: С _II + ΔС _I + ΔС _II = V _I+ π _I, где индексы I и II означают данные для I и II подразделений общественного производства соответственно.

Используя исходные данные по СССР,

а) рассчитайте значения органического строения капитала, нормы прибавочной стоимости и нормы накопления (отношение 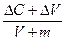) для каждого года;

б) оцените степень достоверности гипотезы о росте органического строения капитала, выраженной формулой: , l > 0;

в) рассчитайте наиболее вероятное значение параметра l и постройте графики динамики органического строения капитала: фактической и расчетной;

г) оцените степень достоверности гипотезы о росте нормы прибавочной стоимости, выражающейся формулой: , m > 0;

д) рассчитайте наиболее вероятное значение параметра m и постройте графики динамики нормы прибавочной стоимости: фактической и расчетной;

е) используя дополнительные данные:

для подгруппы 1 – за 1970 г.,

для подгруппы 2 – за 1965 г.

и предполагая, что органическое строение капитала прирастает в обоих подразделениях одинаковым годовым темпом, равным рассчитанному значению l, а норма прибавочной стоимости ежегодно прирастает темпом, равным рассчитанному значению m, а также, что между подразделениями общественного производства сохраняется сбалансированность, рассчитайте динамику для подгруппы 1 – до 1988 г., для подгруппы 2 – до 1985 г. следующих показателей:

- доли валовой продукции I подразделения общественного производства в сумме стоимости продукции обоих подразделений;

- норм накопления в I и II подразделениях (норма накопления – доля накопления в прибыли, т.е. отношение );

- нормы прибыли;

- потребности обоих подразделений в рабочей силе.

Потребность в рабочей силы оцените относительно, т.е. число занятых в начальном году примите за единицу, а рост занятости приравняйте к росту переменного капитала.

Расчеты проведите при разных значениях доли накопления в национальном доходе (Н – накопление в обоих подразделениях, Н Д – национальный доход), равных:

1) 35%,

2) 25%,

Постройте графики найденных значений.

Сделайте выводы о характере расчетной динамики перечисленных показателей в сравнении с фактической, зависимости этой динамики от уровня нормы накопления.

2) Трехсекторная модель Колемаева:

Предпосылки модели.

Предполагается, что экономика состоит из трех секторов: 0-ой сектор – производство предметов труда (материалов), 1-ый сектор – производство средств труда (основных фондов), 3-ий сектор – производство предметов потребления. Объем выпуска в каждом секторе описывается производственной функцией Кобба-Дугласа. Между секторами имеют место взаимосвязи, описываемые следующими формулами:

1) продукция сектора 1 идет на воспроизводство основных фондов (инвестиции) во всех трех подразделениях: Х ₁ = I ₀ + I ₁ + I ₂ = I; инвестиции (I), в свою очередь, используются в каждом секторе для возмещения износа (mК, m – норма амортизации)и прироста (ΔК) основных фондов;

2) продукция сектора 0 используется в качестве материальных затрат во всех секторах: Х ₀ = а ₀ Х ₀ + а ₁ Х ₁ + а ₂ Х ₂, где а – коэффициент материальных затрат в соответствующем секторе;

3) количество труда, используемое в секторах, в каждом году ограничено:

L ₀ + L ₁+ L ₂ = L.

Процесс экономического роста отражается в этой модели как рост производства в секторах и зависит от распределения инвестиций и труда по секторам, при этом должна соблюдаться сбалансированность между секторами, выраженная в пп.1)–3).

Для расчетов используйте следующие исходные данные (расчет за 1990 г. по России):

- производственные функции секторов экономики:

Сектор 0: ;

Сектор 1: ;

Сектор 2: ;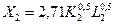

- коэффициенты выбытия основных фондов и прямых материальных затрат:

Сектор 0: m = 0,054, a = 0,39; объем основных фондов = 667,9 млрд. руб.;

Сектор 1: m = 0,072, a = 0,29; объем основных фондов = 178,9 млрд. руб.;

Сектор 2: m = 0,052, a = 0,52; объем основных фондов = 382,7 млрд. руб.;

В материальном производстве занято всего 53,4 млн. чел. Каждый год численность занятых сокращается на 0,3%.

Рассчитайте траекторию развития экономики (рост производства в секторах: 0, 1 и 2) за 10 лет при двух вариантах заданных параметрах распределения ресурсов:

Подгруппа 1:

1) .

2) .

Подгруппа 2:

1) .

2) .

Сделаете вывод о том, как повлияло изменение параметров распределения ресурсов на траекторию развития.

Какая из траекторий лучше и почему?

Лабораторная работа № 4

Статическая модель межотраслевого баланса (8 часов)

I. Используя данные табл. 3 (Приложение 4), рассчитать:

1) технологические коэффициенты модели МОБ (коэффициенты прямых материальных затрат);

2) матрицу (Е - А)^-1 (А – матрица прямых материальных затрат);

3) вектор валовых выпусков Х, (валовой выпуск равняется сумме промежуточного и конечного продуктов, т.е. материальных затрат и добавленной стоимости (ВВП));

4) полные затраты труда, продуктов, зарплаты на единицу выпуска в отраслях 1, 2, 3;

(- вектор полных затрат труда на единицу выпуска рассчитываются по формуле: m = B^Тl, где B^Т – транспонированная матрица (Е – А)^-1, l – вектор коэффициентов прямой трудоемкости;

- матрица коэффициентов полных затрат продуктов – это матрица (Е - А)^-1;

- вектор полных затрат заработной платы на единицу выпуска рассчитывается по формуле: V = (Е - А)^{- 1} v, где v – вектор прямых затрат заработной платы на единицу выпуска);

5) вектор чистого дохода (разность между добавленной стоимостью и заработной платой);

6) Для подгруппы 1:

а) как изменится чистый доход в сельском хозяйстве, если цена на продукцию промышленности вырастет на 10%, а тарифы на услуги транспорта и связи – на 20%?

б) как повлияет рост на 30% зарплаты и соответствующее ему повышение цен в сфере управления, финансов, кредита и страхования на чистый доход в строительстве (при постоянстве остальных цен).

Для подгруппы 2:

а) как изменится чистый доход в ЖКХ, если цена на продукцию промышленности вырастет на 20%, а продукцию строительства – на 15%?

б) как повлияет рост на 20% зарплаты и соответствующее ему повышение цен в сфере здравоохранения, образования и культуры на чистый доход в промышленности (при постоянстве остальных цен)?

II. Используя данные табл. 4 (Приложение 5), рассчитайте:

1) матрицу (Е – А)^-1;

2) полные затраты труда и продуктов на производство единицы продукции в отраслях 1, 2, 3;

3) максимальное число заданных наборов Y (т.е. наборов с той же структурой ВВП) при ограничении на общую численность работников:

для подгруппы 1: L = 50 млн. чел.,

для подгруппы 2: L = 60 млн. чел.

 

Лабораторная работа № 5

Динамические межотраслевые модели экономического роста (8 часов)

Используя данные табл. 5 (а) и б))(Приложение 6), рассчитайте:

1) вектор конечного продукта Y;

2) коэффициенты прямых материальных затрат, прямой трудоемкости и фондоемкости;

3) показатели развития экономики за три года (следующие за данным):

- вектор численности занятых по отраслям экономики, - вектор потребления

при следующих предположениях:

для подгруппы 1:

а) при заданной структуре конечный продукт растет на 5% ежегодно;

б) доля конечной продукции отрасли, идущая на чистое производственное накопление по отраслям: промышленность = 9,3%; сельское хозяйство = 2,8 %; строительство = 42,0%; остальные отрасли = 0;

в) коэффициенты прямой трудоемкости во всех отраслях ежегодно снижаются на 4%; капитальных затрат (K_ij) – растут на 2% (в исходном году они соответствуют коэффициентам, рассчитанным по табл. 5б));

г) общая численность трудовых ресурсов остается постоянной;

для подгруппы 2:

а) при заданной структуре конечный продукт растет на 6% ежегодно;

б) доля конечной продукции отрасли, идущая на чистое производственное накопление по отраслям: промышленность = 10 %; сельское хозяйство = 3,5 %; строительство = 50,0%; остальные отрасли = 0;

в) коэффициенты прямой трудоемкости во всех отраслях ежегодно снижаются на 3,5%; капитальных затрат (K_ij) – растут на 2,4 % (в исходном году они соответствуют коэффициентам, рассчитанным по табл. 3б));

г) общая численность трудовых ресурсов остается постоянной.

4) считая коэффициенты прямых затрат труда, продуктов и фондов постоянными, а структуру Y – определенной как в п. 5б), постройте магистральную модель накопления и найдите соответствующий ей темп роста.

 

Лабораторная работа № 6

Моделирование рынка товаров (8 часов)

Работа выполняется на основе данных табл. 6 (Приложение 7).

1)Модели потребления и сбережения

Используя данные таблицы показателей развития российской экономики, оцените уровень достоверности связей, выраженных перечисленными ниже моделями потребления и сбережения, а также величину параметров этих моделей:

а) кейнсианская модель:

С_t = c ₀ + c_YY_t;

С_t – потребительские расходы домашних хозяйств (строка 2), Y_t – располагаемый доход (сумма строк 2 и 3); постройте функцию сбережений, отвечающую этой модели;

б) модель С. Кузнеца:

С_t = c_YY_t

(смысл обозначений тот же), постройте функцию сбережений, отвечающую этой модели;

в) модель Ф. Модильяни, преобразованная к виду:

D C_t = aY_t + bS_{t – 1}

(S – объем сбережений домашних хозяйств (строка 3); постройте функцию сбережений, отвечающую этой модели;

г) модель М. Фридмена, преобразованная к виду:

С_t = a₁C_{t – 1} + a ₂ Y_t

(обозначения те же), постройте функцию сбережений, отвечающую этой модели;

д) неоклассическая модель:

С_t = a ₀ + a ₁ w_t + a ₂ z_t, ;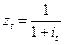

i_t – реальная депозитная ставка процента (рассчитать на основе строк 12 и 13 таблицы), w_t – реальная ставка заработной платы (строка 5); постройте функцию сбережений, отвечающую этой модели.

е) модель Н. Калдора:

( – доля заработной платы в сумме заработной платы и прибыли (строка 6), – доли прибыли в сумме заработной платы и прибыли (строка 7), s_Y – доля сбережений в располагаемом доходе (отношение строки 3 к сумме строк 2 и 3); постройте функцию потребления, отвечающую этой модели;

Для каждой модели раскройте экономический смысл найденных параметров.

Модели инвестиций

а) Неоклассическая модель, приведенная к виду:

I_t = a ₁ X_t + a ₂ K_t,,

где: I_t – инвестиции в основные фонды,

,

Y_t – реальный ВВП (строка 4), d – коэффициент выбытия основных фондов (строка 9), i – реальная кредитная ставка процента (рассчитать на основе строк 11 и 13), K_t – основные фонды. Оценить значимость связей, выраженных моделью, величину параметров а ₁, а ₂. Объяснить экономический смысл этих параметров.

б) Провести аналогичные расчеты для второго варианта неоклассической модели:

I_t = a ₁ X_t + a ₂ K_t,

где: , Y_t – реальный национальный доход (строка 1)

в) Кейнсианская модель, приведенная к виду:

I_t = a ₀ – a ₁ i + a (Y_t – Y_{t – 1}),

где: I_t – инвестиции в основной капитал, i – реальная кредитная ставка процента, Y_t – реальный национальный доход. Оценить значимость связей, выраженных моделью, величину параметров а, а ₀, а ₁. Объяснить экономический смысл параметров модели.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: