Расчет оптимального портфеля ценных бумаг

На основе данных табл. 8 (Приложение 9) за период с августа 2005 г. по ноябрь 2006 г. (строки 1-16) рассчитайте доходность ценных бумаг в разные моменты времени и оптимальную структуру портфеля, используя следующие модели:

а) Портфель составлен из рисковых активов. Доходность портфеля задана:

- для подгруппы 1 – 1,5% в месяц;

- для подгруппы 2 –1% в месяц.

Минимизировать риск.

б) Портфель составлен из рисковых и безрискового актива (доходность безрискового актива – 0,3% в месяц). Ожидаемая доходность портфеля:

- для подгруппы 1 – 1,2% в месяц;

- для подгруппы 2 –1,5% в месяц.

Минимизировать риск.

в) Портфель составлен из рисковых активов. Функция М. Рубинштейна (целевая функция) задана выражением:

U = ym_P – s_P²,

где: y = 1,5 (для подгруппы 1) и 1,2 (для подгруппы 2), m_P и s_P ² – математическое ожидание и дисперсия доходности портфеля.

г) Минимизируется степень риска портфеля рисковых активов (y = 0).

д) При заданной степени риска:

- для подгруппы 1 – 20%;

- для подгруппы 2 – 15%

максимизируется математическое ожидание доходности портфеля рисковых бумаг.

е) Равномерное распределение вложений («наивная диверсификация»).

 

Лабораторная работа № 8

Моделирование безработицы и инфляции (8 часов)

1) Используя данные табл. 9 (приложение 10), оцените степень достоверности связей, выраженных перечисленными ниже моделями, а также величину параметров этих моделей:

а) Неоклассическая модель спроса на труд (строки 1, 4, 7, 8):

,

где: K_t – объем основных фондов, (w / P) _t – реальная ставка заработной платы, а ₀ и а ₁ – постоянные. В качестве объема спроса на труд взять численность занятых плюс число вакансий.

б) Неоклассическая модель предложения труда (строки 2, 3, 7, 9)

Два варианта:

,

где – межвременное соотношение реальных ставок заработной платы, id – реальная депозитная ставка процента, а, b, а ₀, а ₁ – постоянные. В качестве объема предложения труда взять число безработных плюс число занятых. Для расчета реальной ставки процента воспользоваться дефлятором (строка 12).

в) Кейнсианская модель спроса на труд (строки 1, 2, 4, 8):

Три варианта:

;

;

где; L ₀, а, b, а ₁, а ₂ – постоянные, Y_t – реальный ВВП, К_t – основные фонды. В качестве объема спроса на труд взять численность занятых плюс число вакансий.

г) «Естественная» безработица (строки 2, 3, 4, 5, 6):

Определите по годам уровень естественной безработицы:

– как отношение числа вакансий к числу экономически активного населения и

– по монетаристской формуле:

,

где: d - отношение числа уволенных к числу занятых, g – отношение числа принятых на работу к числу безработных.

Сравните уровень и динамику этих двух показателей.

2) Используя данные табл. 10 (Приложение 11), оцените степень достоверности связей, выраженных перечисленными ниже моделями, а также наиболее вероятную величину параметров этих моделей:

а) Закон Окуня

Использовать формулу: , которая предполагает, что потенциальный объем выпуска прямо пропорционален предложению труда (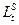), в качестве предложения труда взять численность экономически активного населения; а ₀ и а ₁ – постоянные, Y_t – реальный объем ВВП, u_t и u_t* – фактический и «естественный» уровни безработицы.

б) Кривая Филлипса

,

ожидаемый уровень инфляции оценить по формуле:

,

b, l ₁, l ₂, l ₃ – постоянные множители.

в) Динамические модели совокупного предложения и спроса

где а, b, с, h – постоянные параметры. Уровень ожидаемой инфляции и ее прирост оценивается по той же формуле, что и в предыдущем пункте, потенциальный объем ВВП оценивается по формуле: (b – постоянный множитель), π_t и m_t – темпы инфляции и прироста денежной массы, Y_t – реальный ВВП, 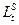– объем предложения труда (численность экономически активного населения).

г) Монетаристская модель инфляции

p_t – p_{t – 1} = m_t – m_{t – 1} – (y_t – y_{t – 1}). В левой части – логарифм темпов роста цен, в правой – разность логарифмов темпа роста денежной массы и реального ВВП.

 

Лабораторная работа № 9

Моделирование социальных процессов (4 часа)

1) На основе данных табл. 11 (Приложение 12) для всех лет, по которым приведены стат. данные, построить график кривой Лоренца и рассчитать величину индекса Джини. Затем построить график, отражающий изменение индекса Джини во времени. Проанализировать его и сделать выводы относительно дифференциации доходов населения РФ.

Рассчитать индекс Джини по децильным группам, используя данные табл. 17 (Приложение 18), взяв вместо величины дохода группы размер ее расходов и определив долю расходов каждой группы в общей сумме расходов.

2) На основе данных таблиц 12, 13, 14 и 15 (Приложения 13, 14, 15, 16) для всех лет, по которым приведены данные, рассчитать коэффициенты, характеризующие степень дифференциации средней заработной платы по видам деятельности (табл. 12) и по субъектам РФ (табл. 13), а также степень дифференциации среднедушевых доходов (табл. 14) и среднего размера пенсии по субъектам РФ (табл. 15). Построить графики динамики рассчитанных коэффициентов во времени, провести их анализ и сделать выводы о динамике степени различий в уровне соответствующих показателей.

Для расчета указанных коэффициентов дифференциации применить следующую формулу:

,

где: у – значение коэффициента, N – число наблюдений соответствующего показателя (заработной платы, дохода, пенсии), i и j – номера наблюдений, 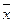– среднее значение соответствующего показателя (заработной платы, дохода, пенсии). (Суммирование идет по всем значениям параметра).

3) Пользуясь данными табл. 6, проанализировать зависимость структуры расходов домашних хозяйств от уровня их доходов в 2005 г. В качестве показателя уровня дохода взять долю соответствующей 20-процентной группы домашних хозяйств в зависимости от уровня их доходов в 2005 г. качестве населения в общей сумме доходов (см. табл. 11). Использовать модели линейной и степенной регрессий:

где: у – доля соответствующего элемента (напр., расходов на продукты питания, или на алкогольные напитки и т.п.) в структуре расходов; х – уровень дохода.

Аналогичные вычисления проведите по данным табл. 17 (Приложение 18) (децильные группы).

Сделать выводы о наличии или отсутствии рассмотренных зависимостей, их значимости.

4) Используя данные табл. 18, 19 и 20 (приложения 19, 20 и 21), проведите анализ зависимости объема потребления ряда основных видов потребительских товаров от уровня реальных доходов населения и цен (по тем товарам, где имеются сведения о ценах). Для этого необходимо вначале привести все индексы цен к уровню 2000 г., взяв его за единицу. Затем разделить эти индексы на общий индекс цен продовольственных товаров за соответствующий год, – с тем, чтобы определить относительное удорожание или удешевление данного вида товаров по сравнению со всеми продовольственными товарами в том или ином году.

В качестве эконометрических моделей использовать линейную и степенную регрессии:

где: у – объем потребления товара, I - размер дохода, P – уровень цены товара (индекс цен, приведенный к базовому периоду), a, b и c – коэффициенты. Для тех товаров, по которым отсутствуют сведения о ценах, расчеты сделайте по однофакторным моделям.

Определите значимые факторы и оценки параметров моделей.

Прокомментируйте результаты расчетов. Какие из найденных зависимостей могут быть использованы для прогнозирования объемов потребления товаров, если известен достоверный прогноз роста доходов?

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: