Тема 1 . Задачи математического программирования

Методы и модели анализа динамики экономических процессов

А информатики и компьютерных технологий

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ

 

 

Методические указания к лабораторным работам

для студентов направлений подготовки бакалавриата

120700, 080100, 080200

 

САНКТ-ПЕТЕРБУРГ

 

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Национальный минерально-сырьевой университет «Горный»

 

Кафедра информатики и компьютерных технологий

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ

Методические указания к лабораторным работам

для студентов направлений подготовки бакалавриата

120700, 080100, 080200

 

САНКТ-ПЕТЕРБУРГ

 

УДК 519.86:622.3.012 (075.83)

Линейное программирование. Оптимальное распределение ресурсов. Методические указания для выполнения лабораторных работ для студентов направлений подготовки бакалавриата 120700, 080100 и 080200./НМСУ «Горный». Сост. В.В. Беляев, Т.Р. Косовцева. СПб, 2013., 62 с.

 

Методические указания содержат необходимые теоретические сведения по решению задач линейного программирования аналитическими (симплекс-метод) и численными методами. Приведены примеры решения типовых задач по определению и анализу оптимального плана выпуска продукции предприятия.

Предназначены для студентов направлений подготовки бакалавриата 120700 «Землеустройство и кадастры», 080100 «Экономика», 080200 «Менеджмент»» дневной и заочной формы обучения,, изучающих дисциплины «Экономико-математические методы и моделирование», «Методы оптимальных решений», «Методы принятия управленческих решений».

Табл. 13. Рис.32. Библиогр.: 2 назв.

 

 

Научный редактор - доц. Прудинский Г.А.

 

© Национальный минерально-сырьевой университет «Горный», 2013 г.

 

Введение

Любой человек в течение всей своей жизни вынужден принимать решение, как в житейских, так и в производственных ситуациях. Как правило, существует множество вариантов решения одной и той же проблемы. Среди этого множе­ства желательно найти наилучший в некотором смысле вариант с учетом ограничений, наличие которых обусловлено лимитированостью природных, эко­номических и технологических ресурсов. Математические методы, позволяющие применять для анализа и синтеза экономических ситуаций и систем современную вычислительную технику, объединяются под общим названием — математическое программирование.

Математическое программирование — область мате­матики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограниче­ниями, т. е. задач на экстремум функции многих пере­менных с ограничениями на область изменения этих переменных.

Функцию, которая отражает качество принимаемого решения, называют целевой или показателем эффективности или критерием опти­мальности. Экономические возможности формализуются в виде системы ограничений. Ограничения, как правило, задаются в виде системы уравнений и неравенств.

Один из разделов математического программирования называется линейным программированием. К задачам линейного программирования относятся задачи, в которых целевая функция и ограничения выражаются линейными соотношениями. Методы и модели линейного программирования широко применяются при оптимизации процессов во множестве отраслей народного хозяйства. Особенно широкое применение методы и модели линейного програм­мирования получили при решении задач экономии ресур­сов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов), производственно-транспорт­ных и других задач.

Эффективным методом решения данного класса задач является симплекс-метод.

 

ЛАБОРАТОРНАЯ РАБОТА 1

Тема 1. ЗАДАЧИ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ

 

Цель работы:

· изучить основные понятия линейного программирования;

· освоить графический метод решения простейших задач линейного программирования;

· научиться использовать сим­плексный метод с искусственным базисом на примере задачи о диете.

1. Основная задача линейного программирования

1.1. Основные формулы и определения

В каноническом виде задача линейного программирования (ЛП) формулируется следующим образом.

Найти такой набор 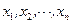, который является решением системы

(1.1)

удовлетворяет соотношению

(1.2)

и обеспечивает максимум (минимум) линейной функции

(1.3)

Соотношения (1.1) принято называть фазовыми ограничениями, соотношения (1.2) – естественными ограничениями.

Функцию F принято называть целевой функцией.

Система ограничений всегда может быть приведена к каноническому виду.

Если ограничения заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих) ресурсов.

Так, например, в неравенстве достаточно добавить к левой части некоторую величину x_n+1³0 и получится равенство: .

Чтобы балансовые переменные не влияли на искомый оптимум, их вводят в целевую функцию (1.1) с нулевыми коэффициентами.

В дальнейшем будет рассматриваться только задача на максимизацию. Если необходимо решить задачу на минимизацию линейной формы, то коэффициенты целевой функции следует умножить на (-1) и решать эту новую задачу на максимум. Искомый минимум целевой функции получается умножением найденного максимального значения на (-1), т.е. .

Задачу ЛП, определяемую соотношениями (1.1)-(1.3), можно записать в матричном виде:

,

,

,

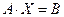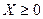где , , ,

.

В дальнейшем при анализе задачи также используется расширенная матрица системы (1.1) 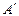, которая составляется из матрицы А и вектора В.

Пример 1. Задача о диете.

Составить задачу ЛП, позволяющую оптимизировать расход кормов, и привести ее к каноническому виду.

Для откорма животных употребляют два вида кормов; стоимость 1 кг корма I вида - 5 у.е., а корма - II вида 2 у.е. В каждом килограмме корма I вида содержится 5 ед. питательного вещества А, 2.5 ед. питательного вещества B и 1 ед. питательного вещества C. В каждом килограмме корма II вида содержится соответственно 3, 3 и 1.3 ед. Суточный рацион предусматривает питательных единиц A не менее 225 ед., типа B - не менее 150 ед. и типа C - не менее 80 ед. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты были минимальны?

Решение

Построим математическую модель данной задачи. Обозначим через x ₁ и x ₂ количество кормов I и II вида соответственно. Тогда суммарная стоимость кормов будет равна 5 x ₁ +2 x ₂. Поэтому целевая функция будет иметь вид:

(1.4)

Ограничения по содержанию питательных веществ в рационе будут иметь вид:

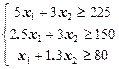
	(1.5)
	(1.6)

Соотношения (1.4)-(1.6) корректно определяют задачу ЛП, но предложенная форма записи не является канонической. Для приведения задачи к этой форме домножим ЦФ (1.4) на –1, в результате получим новую ЦФ (1.7). Для преобразования фазовых ограничений (1.5) к канонической форме введем положительные балансовые переменные x ₃, x ₄ и x ₅. Тогда фазовые ограничения примут вид (1.8), а естественные - вид (1.9).

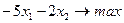
(1.7)

 

	(1.8)
	(1.9)

Соотношения (1.7) – (1.9) определяют задачу ЛП в канонической форме.

1.2. Симплекс-метод

1.2.1. Геометрическая интерпретация

Геометрическое истолкование симплекс-метода наиболее просто может быть проиллюстрировано в случае двух переменных.

Положение 1.

Каждое неравенство с двумя переменными x ₁ и x ₂ определяет полуплоскость в системе координат x ₁ 0 x ₂.

Положение 2.

В случае, когда задана система неравенств

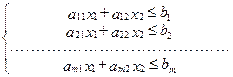
(1.10)

то она определяет многоугольную область D на плоскости, которая является результатом пересечения m полуплоскостей. Область D называется областью решений системы неравенств. Область D может быть ограниченной, неограниченной или пустой. Область решений D обладает важным свойством – она является выпуклой.

Определение 1. Область называется выпуклой, если она вместе с любыми двумя точками содержит весь отрезок их соединяющий.

Определение 2. Прямая называется опорной по отношению к области, если:

1) имеет с областью по крайней мере одну общую точку;

2) вся область лежит по одну сторону от этой прямой.

Положение 3. Пусть задана линейная функция

(1.11)

Для каждой точки плоскости в системе координат x ₁ 0 x ₂. функция F принимает фиксированное значение F=F ₁.

Определение 3. Множество точек, в которых функция двух переменных принимает фиксированное значение, называется линией уровня.

Линия уровня для линейной функции – прямая, которая определяется уравнением . Придавая F ₁ различные значения, получим различные линии уровня.

Все линии уровня (для линейной функции) параллельны между собой.

Нормаль к линии уровня определяется через градиент функции. Градиент произвольной функции двух переменных f (x _1, x ₂) может быть вычислен по формуле

,

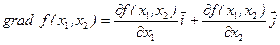(1.12)

поэтому градиент линейной функции определяется уравнением , т.е. градиент может быть задан вектором 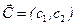, выходящим из начала координат.

Градиент указывает направление наибыстрейшего роста функции в данной точке.

Положение 4. Графическое решение задачи ЛП, определяемой фазовыми ограничениями (1.10), естественными ограничениями и целевой функцией (1.11), основано на мысленном эксперименте по перемещению линии уровня относительно области допустимых решений D. Область допустимых решений D задачи ЛП – это множество точек, координаты которых удовлетворяют фазовым и естественным ограничениям. Допустим, множество D ограничено. Пусть при движении прямой F ₁ в положительном направлении вектора она впервые встретится с многоугольником решений в его вершине, тогда в этом положении прямая F ₁ становится опорной, и на этой прямой функция F принимает наименьшее значение. При дальнейшем движении в том же направлении прямая F ₁ пройдет через другую вершину многоугольника решений (выходя из области решений), и станет также опорной прямой; на ней функция F принимает наибольшее значение среди всех значений, принимаемых на многоугольнике решений.

Таким образом, максимизация линейной функции на многоугольнике решений достигается в точке пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору .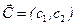

Положение 5. Существование решения и количество решений задачи ЛП основано на анализе взаимного расположения области допустимых решений D и линии уровня.

Если область D ограничена, то возможны два варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – множество решений (вся сторона многоугольника).

Если область D не ограничена, то возможны три варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – имеется множество решений;

В) не существует опорной прямой (в направлении роста функции) - множество решений пусто (нет решений).

Пример 2.

Решить графически задачу ЛП (1.13)-(1.15).

	(1.13)
	(1.14)
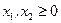
	(1.15)

 

Решение

Построим область допустимых решений.

Первое неравенство системы (1.14) задает полуплоскость, границей которой является прямая y ₁, определяемая равенством 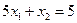. Построим эту прямую на координатной плоскости x ₁ 0 x ₂ (рис.1.1), искомой полуплоскостью (она заштрихована) будет, та, которая лежит выше этой прямой.

Второе неравенство задает полуплоскость, границей которой является прямая y ₂, определяемая равенством . Также построим прямую y ₂ на координатной плоскости и заштрихуем соответствующую полуплоскость.

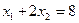Аналогично построим полуплоскости, соответствующие неравенствам три и четыре, их границы y ₃ и y ₄, определяются уравнениями и соответственно.

Пересечение этих четырех плоскостей и плоскостей естественных ограничений определяют область допустимых решений D.

Рис. 1.1

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору . Линия F 1, проходящая через начало координат, соответствует значению 1, поскольку 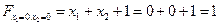. Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника D соответствует положению F 3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Продолжим движение линии уровня до выхода из множества D. Этому положению соответствует положение F 7. Рассмотрим крайнюю точку M, которая является точкой пересечения прямых y ₃ и y ₄, ее координаты можно определить как решение линейной системы.

Решением системы является пара чисел x ₁=4 x ₂=2. Этому решению соответствует искомое максимальное значение линейной функции

.

Таким образом, F _max=7 при x ₁=4 x ₂=2.

Вывод. В данном случае линейная функция достигает своего максимального значения в вершине множества решений.

 

Пример 3.

Решить графически задачу ЛП (1.16) – (1.18).

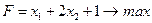
	(1.16)
	(1.17)
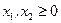
	(1.18)

Решение

Заметим, что система фазовых ограничений (1.17) совпадает с системой (1.14). Поэтому область допустимых решений D будет той же самой, что и в примере 2 (рис.1.2).

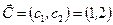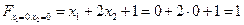Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору . Линия F1, проходящая через начало координат, соответствует значению 1, поскольку . Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника соответствует положению F 3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Продолжим движение линии уровня до выхода из множества D,. этому положению соответствует положение F 8. Заметим, что линия уровня параллельна стороне MN, поэтому решением является множество точек лежащих между крайними точками M и N, Точка M является точкой пересечения прямых y ₃ и y ₄, ее координаты можно определить как решение линейной системы.

Решением этой системы является пара чисел x ₁=4, x ₂=2. Эта пара чисел определяет координаты точки М и в ней достигается искомое максимальное значение линейной функции, равное

.

Таким образом, F _max=9, при x ₁=4, x ₂=2.

Точка N является точкой пересечения прямых y ₁ и y ₄; ее координаты можно определить как решение линейной системы

 

Рис.1.2

Решением полученной системы является пара чисел x ₁=2/9, x ₂=35/9, которые определяют координаты точки N, значение целевой функции в которой равно

.

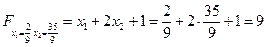Таким образом, значение в точке N совпадает со значением в точке M. F _max=9, при x ₁=2/9, x ₂=35/9.

Координаты всех точек, лежащих между M и N можно записать в виде

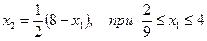
Значение функции во всех этих точках равно 9.

Вывод. В данном случае линейная функция достигает своего максимального значения во всех точках ребра MN множества решений D.

Пример 4.

Решить графически задачу ЛП (1.19) – (1.21).

	(1.19)
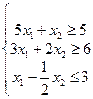
	(1.20)
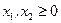
	(1.21)

Решение.

Построим область допустимых решений D (рис. 1.3).

Построение области аналогично примеру 2, но в этом построении отсутствует прямая y ₄.

Пересечение трех полуплоскостей с учетом естественных ограничений определяет неограниченную область допустимых решений D.

Рис. 1.3

 

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору– . Линия F 1, проходящая через начало координат, соответствует значению 1, поскольку .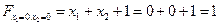

Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника соответствует положению F 3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Заметим, что многогранник незамкнут в направлении роста целевой функции, поэтому целевая функция не имеет максимума. Это объясняется тем, что для любой линии уровня найдется другая линия уровня, лежащая в направлении вектора , которой соответствует большее значение функции.

Вывод. Целевая функция не ограничена, если многогранник незамкнут в направлении роста целевой функции.

Пример 5.

Решить графически задачу ЛП (1.22) – (1.24).

	(1.22)
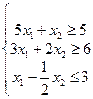
	(1.23)
	(1.24)

Решение

Построим область допустимых решений D (рис. 1.4), она совпадает с областью в примере 3.

Заметим, что вектор-градиент направлен в противоположную сторону (по сравнению с рис. 1.3). Максимум достигается в единственной точке Р, являющейся точкой пересечения оси x₁ и прямой y ₂.

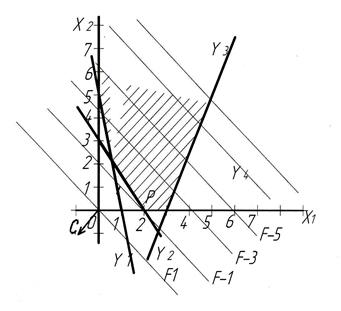
Рис. 1.4

Координаты точки Р можно определить, решив систему уравнений:

Ее решение x ₁=2, x ₂=0, значение функции в этой точке равно

Вывод. Задача ЛП имеет решение, когда многогранник замкнут в направлении роста целевой функции.

Рассмотренные примеры иллюстрируют четыре варианта Положения 5.

1.2.2. Основная идея симплекс-метода

Если ранг матрицы А системы (1.1) и ранг расширенной матрицы системы равен r(r£m), то r переменных 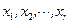могут быть выражены через остальные переменные:

(1.25)

Переменные (неизвестные) называются базисными, а весь набор () – базисом, остальные переменные называются свободными. Система ограничений (1.25) называется системой приведенной к единичному базису.

Отметим важнейшие условия наличия единичного базиса:

· от каждого уравнения в него входит одна и только одна неизвестная;

· каждая переменная из этого набора входит с коэффициентом +1 и отсутствует в остальных уравнениях;

· все значения ,

Подставляя в линейную форму F (1.3) вместо базисных переменных их выражения через свободные переменные из системы (1.25), получим:

(1.26)

Полагая все свободные переменные равными нулю, найдем значения базисных переменных: 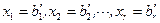. Если все значения , решение () системы ограничений является допустимым. Такое допустимое решение называется базисным или опорным, обозначим его через . Для полученного базисного решения значение целевой функции . Решение задачи при помощи симплекс-метода подразумевает ряд шагов, состоящих в том, что от данного базиса переходим к другому базису с таким расчетом, чтобы значение целевой функции F увеличивалось или, по крайней мере, не уменьшалось, т.е. .

Геометрическая интерпретация симплекс-метода состоит в том, что аналитическому переходу от одного базиса к другому соответствует переход от одной вершины многогранника (множества допустимых решений) к другой, в которой целевая функция имеет не меньшее значение. Этот факт основан на том, что вершинам многоугольника множества допустимых решений соответствуют опорные решения системы ограничений.

Решение симплекс-методом заканчивается, когда среди опорных решений будет найдено такое, которое обеспечивает максимум линейной формы (1.3). Такое решение называется оптимальным.

1.2.3. Реализация симплекс-метода (простейший случай)

Рассмотрим идею симплекс-метода на конкретном примере:

	(1.27)
	(1.28)
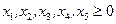
	(1.29)

 

Решение

Данная система уравнений совместна, так как ранги матрицы системы

и расширенной матрицы

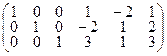
совпадают и равны 3. Следовательно, три переменные (базисные) можно линейно выразить через две свободные переменные. Выразим, например, x₁, x₂ и x₃ через x₄ и x₅, т.е. приведем систему к единичному базису:

(1.30)

Линейная форма уже выражена через x₄ и x₅.

При x ₄ =0 и x ₅= 0, найдем значения базисных переменных x₁= 1, x₂ =2 и x₃= 3.

Таким образом, первое допустимое решение имеет вид x₁= 1 ,x₂ =2, x₃= 3, x₄ = 0, x₅= 0 или (1,2,3,0,0). При найденном допустимом решении линейная форма F имеет значение 0, т.е. F₁= 0.

Теперь попытаемся увеличить значение F:

- увеличение x₄ уменьшит F, так как перед x₄ стоит отрицательный коэффициент, а увеличение x₅ даст увеличение;

- будем увеличивать x₅ таким образом, чтобы одна из базисных переменных (x ₁ или x₂ или x₃)обратилась в ноль, а остальные базисные переменные оставались бы неотрицательными.

Анализируя первое уравнение системы (1.30), приходим к выводу, что x₅ можно увеличить неограниченно. При этом x₁ остается положительным и никогда необратиться в ноль. Из второго уравнения системы (1.30) следует, что x₅ можно увеличить до 2 (больше увеличивать нельзя, т.к. x₂ станет отрицательным). Из третьего уравнения системы (1.24) следует, что x₅ можно увеличить до 3. Принимая во внимание приведенный анализ, приходим к выводу, что x₅= 2.

Таким образом, получим второе допустимое решение x₁= 5, x₂= 0, x₃= 1, x₄ = 0, x₅= 2 или (5,0,1,0,2).

Значение линейной формы F при этом допустимом решении равно F₂= 2, т.е. значение целевой функции увеличилось.

Примем за свободные переменные x₂ и x₄., т.е. те переменные, которые в этом решении равны 0. С этой целью из второго уравнения системы (1.27) выразим x₅ .

Получим . Тогда

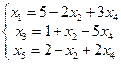
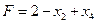
(1.31)

Для увеличения значения F будем увеличивать x₄. Проведя аналогичный анализ системы (1.31), заключаем, что x₄ можно увеличить до 1/5 (следует из рассмотрения второго уравнения системы (1.31)). Таким образом, получим третье допустимое решение x₁= 28/5, x₂= 0, x₃= 0, x₄= 1/5, x₅= 12/5 или (28/5, 0, 0, 1/5, 12/5). Значение линейной формы F при этом допустимом решении равно F₃=11/5, т.е. значение целевой функции увеличилось.

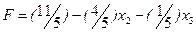
(1.32)

 

Так как в последней линейной форме обе свободные переменные входят с отрицательными коэффициентами, то наибольшее значение достигается при x₂ =0, x₃= 0.

Из этого следует, что решение (28/5, 0, 0, 1/5, 12/5) является оптимальным и F_max= 11/5.

Для того, чтобы упростить трудоемкие операции по пересчету коэффициентов и перезаписи системы ограничений, можно выполнять преобразования специальной симплекс-таблицы.

Симплексные таблицы

Для составления такой таблицы систему фазовых ограничений и целевую функцию необходимо записать в стандартной форме, т.е. сведенной к единичному базису:

	(1.33)
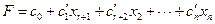
	(1.34)

 

В виде таблицы (табл.1.1) эти данные можно представить так:

Таблица 1.1

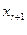
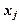
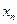
Базисные переменные		…		…			…		…		Свободные члены
		…		…					…
…		…		…		…		…	…	…	…
		…		…					…
…	…	…	…	…	…	…	…	…	…	…	….
		…		…					…
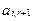
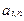
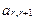
F		…		…					…

Заметим, что в строку с целевой функцией коэффициенты записываются с противоположным знаком .

Каждой итерации соответствует преобразование симплексной таблицы, в результате которого получается новое базисное решение, которому соответствует первый столбец.

Правила преобразования симплексной таблицы.

1. Выбирают разрешающий столбец из условия 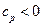и хотя бы один элемент .

2. Выбирают q -ю разрешающую строку из условия

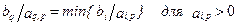
Элемент , стоящий на пересечении разрешающего (с индексом p) столбца и разрешающей (с индексом q) строки, называется разрешающим элементом.

3. В состав базисных переменных вводят переменную , которую записывают в строку с номером q.

4. Производят пересчет элементов разрешающей q -й строки по формуле

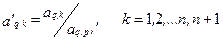
В результате преобразования получают единицу на месте разрешающего элемента.

5. Вычисляют элементы всех остальных строк (при k¹p) по формуле:

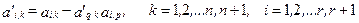
Строке с номером r+ 1 соответствует строка целевой функции, столбцу с номером n+ 1 соответствует столбец свободных членов.

Другими словами, умножая разрешающую строку на подходящие числа и прибавляя ее к остальным строкам, добиваются, чтобы остальные элементы разрешающего столбца стали равными нулю.

6. Далее анализируем полученную таблицу. Если решение получено или выяснено, что его нет, процесс решения закончен. Иначе переходим к пункту 1.

Анализ базируется на основной теореме симплекс-метода.

Теорема.

Если после выполнения очередной итерации (преобразования):

1) найдется хотя бы один отрицательный коэффициент , и в каждом столбце с таким коэффициентом окажется хотя бы один положительный элемент, то можно улучшить решение, выполнив следующую итерацию;

2) найдется хотя бы один отрицательный коэффициент , и в соответствующем столбце не содержится положительных элементов, то функция F не ограничена в области допустимых решений;

3) все коэффициенты окажутся неотрицательными, то оптимальное решение достигнуто.

Рассмотрим решение той же задачи (1.27) - (1.29) с помощью симплекс-таблиц.

Исходная симплекс-таблица, определяемая соотношениями (1.27) - (1.29) показана на рис. 1.5.

 

Базисные переменные	x1	x2	x3	x4	x5	Свободные члены
x1					-2
x2				-2
x3
F					-1

Рис.1.5. Исходная симплекс таблица

Заметим, что целевая функция в данном примере может быть записана в виде 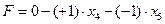, что соответствует виду (1.34). В качестве разрешающего столбца выберем столбец, соответствующий x ₅ , поскольку в нем в строке с целевой функцией стоит отрицательный элемент (– 1).

Для определения разрешающей строки заполним вспомогательный столбец (рис. 1.6).

Первая клетка в этом столбце оставлена пустой, поскольку в соответствующей клетке столбца x₅ стоит отрицательный элемент (– 2).

Из этого столбца выбираем минимальное значение min{2;3}=2; это значение стоит во второй строке, поэтому берем её в качестве разрешающей.

Базисные переменные	x1	x2	x3	x4	x5	Свобод-ные члены	Вспомога-тельный
x1					-2
x2				-2			2/1=2
x3							3/1=3
F					-1

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: