 |
Продолжение примера 1. Решение задачи о диете.
|
|
|
|
В примере 1 была составлена задача о диете (1.4)-(1.6) и она приведена к канонической форме (1.7)-(1.9). При этом ни одно из уравнений фазовых ограничений (1.8) не имеет предпочтительной формы, поэтому необходимо составить и решить М -задачу.
М -задача запишется так:
| (1.39) |
| (1.40) |
| (1.41) |
Выразим ЦФ через свободные переменные 
. Для вычисления 
сложим все уравнения фазовых ограничений: 
или
.
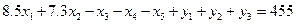Откуда следует
,
поэтому ЦФ (1.39) запишется в виде:
| (1.42) |
Приведя подобные коэффициенты при свободных переменных , получим ЦФ
| (1.43) |
Решим задачу ЛП (1.40), (1.41), (1.43) с помощью симплекс-метода, взяв в качестве базисных переменных искусственные переменные 
.
Решение, оформленное с помощью MS Excel, приведено ниже на рис.1.10-1.12. Существенным отличием от симплекс-таблиц, приведенных ранее, является выделение двух строк для записи ЦФ. Коэффициенты в ЦФ имеют вид 
. Первая строка содержит множители, стоящие перед постоянной М, т.е. 
, вторая строка 
. Обе строки будем преобразовывать по тем же правилам, что и остальные строки.
Поскольку 
сколь угодно большое положительное число, очевидно, что знак коэффициента 
полностью определяется знаком . Это определяет ход решения М -задачи:
1) сначала избавляемся от отрицательных коэффициентов в первой строке ЦФ (в таблицах эта строка помечена буквой «М»);
2) далее избавляемся от отрицательных коэффициентов во второй строке ЦФ (в таблицах эта строка помечена буквой «1»), при условии, что в этом столбце строки «М» содержится ноль.
Результат решения задачи после третьей итерации приведен на рис.1.12 в диапазоне ячеек A33:J39. Целевая функция имеет вид
| (1.44) |
Очевидно, что дальнейшее увеличение ЦФ может быть достигнуто за счет ввода 
в базис, поскольку при достаточно больших М коэффициенты при 
отрицательны.
|
|
|
Результат решения задачи после четвертой итерации приведен на рис.1.12 в диапазоне ячеек A41:J47. Целевая функция имеет вид
| (1.45) |
Очевидно, что все коэффициенты при свободных переменных отрицательны, при достаточно больших М. Оговорка относительно М существенна, поскольку коэффициент при будет отрицательным, когда М, например, больше 1. Таким образом, решение М -задачи получено, а значение ЦФ функции равно -150.
Поскольку в оптимальном плане М -задачи 
все искусственные переменные 
, то, в соответствие с теоремой, план
является оптимальным планом исходной задачи (1.4)-(1.6).
Таким образом, оптимальным решением задачи о диете является план, который предусматривает покупку кормов только второго вида в количестве 75 единиц, стоимость диеты равна 150 у.е. При этом перекорм по питательному веществу B равен 75 единиц, а по питательному веществу C равен 17.5 единиц, по питательному веществу A перекорма нет.
Рис.1.10. Решение М -задачи (начало)
Рис.1.11. Решение М -задачи (продолжение).
Рис.1.12. Решение М -задачи (окончание).
Задание
Каждый вариант содержит одну задачу.
Задача о диете.
Для откорма животных употребляют два вида кормов; стоимость 1 кг корма I вида- 
у.е., а корма - II вида 
у.е. В каждом килограмме корма I вида содержится 5 ед. питательного вещества А, 2.5 ед. питательного вещества B и 1 ед. питательного вещества C. В каждом килограмме корма II вида содержится соответственно 3, 4 и 1.5 ед. Суточный рацион предусматривает питательных единиц A не менее 
ед., типа B - не менее 
150 ед. и типа C - не менее 
ед. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты были минимальны, а животные получили питательных веществ А, B и C вида не меньше указанных нормативов?
Указание. Значения 
и 
равны 0.4 и -0.4 соответственно или задаются преподавателем, 
- номер студента в списке группы.
|
|
|
Исполнение: Решить задачу тремя способами:
- графическим методом;
- симплекс-методом;
- с помощью надстройки «Поиск решения» в MS Excel.
Сравнить полученные результаты.
ЛАБОРАТОРНАЯ РАБОТА 2
|
|
|
