Тема: задача о распределении ресурсов

Цель работы: Научиться строить модель задачи об оптимальном плане выпуска продукции в условиях ограниченности ресурсов. Получить понятие о двойственной задаче линейного программирования и её экономическом смысле. Научиться использовать понятие устойчивости для экономического анализа полученного решения.

2. Задача об оптимальном выпуске продукции

2.1. Постановка задачи, основные формулы

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования, которая записывается следующим образом:

	(2.1)
	(2.2)
	(2.3)

Здесь (2.1) - целевая функция; (2.2) - система ограничений; (2.3) - естественные ограничения;

x_j – количество выпускаемой продукции j -го типа, j =1,2, … n;

b_i - количество ресурса в наличии i -го вида (имеющийся запас), i =1,2,…, m;

a_ij - норма расхода i- го ресурса для выпуска единицы продукции j- го типа;

c_j - прибыль, получаемая от реализации единицы продукции j -го типа.

Значение целевой функции - это суммарная величина прибыли от реализации продукции, выпущенной в объемах x₁, x₂,...x_n. Левая часть неравенства (2.2) представляет собой общее количество ресурса i, используемого в соответствии с планом, правая часть - это имеющийся запас.

Каждой задаче линейного программирования соответствует двойственная задача, которая записывается по следующим правилам:

1. Каждому i -му ограничению исходной задачи соответствует переменная двойственной задачи u_i (двойственная переменная)

2. Каждой j -ой переменной исходной задачи соответствует ограничение двойственной. Матрица коэффициентов ограничений двойственной задачи является транспонированной матрицей ограничений исходной. Если в исходной задаче ограничения имеют знак £, то в двойственной - ³.

3. Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи

4. Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума:

	(2.4)
	(2.5)
	(2.6)

Можно доказать следующие утверждения:

§ Для оптимального решения значения целевых функций прямой и двойственной задач совпадают (maxF = minG).

§ Если соотношение maxF = minG записать в форме , то видно, что двойственная переменная u_i является коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении ресурса b_i на единицу. В литературе по оптимизации двойственные переменные принято называть двойственными оценками. В отчетах, полученных с помощью табличного процессора MS Excel, двойственная оценка называется теневой ценой.

§ Теневая цена ресурса отлична от нуля (точнее, больше нуля) только для тех видов ресурсов, которые используются полностью, т.е. ограничения (2.2) превращаются в равенства.

§ Симметричность прямой и двойственной задач заключается в том, что значения теневой цены в прямой задаче совпадают с решением двойственной и наоборот.

§ В теории ЛП также рассматриваются дополнительные двойственные переменные, которые в отчетах MS Excel называются нормированной стоимостью. Каждой основной переменной x _j соответствует своя нормированная стоимость v_j. Известно, что если x_j=0 (т.е. продукцию j- го типа выпускать не целесообразно), то v_j отлична от нуля (точнее v_j<0) и наоборот, если x_j>0 (продукцию выпускать целесообразно), то соответствующее v_j=0. Экономический смысл нормированной стоимости - это величина, которая показывает, на сколько уменьшится значение суммарной прибыли (ЦФ), при принудительном выпуске этой продукции.

2.2. Изменение оптимального плана выпуска при изменении величин прибыли и запасов ресурсов

Большое значение в экономическом анализе результата решения играет понятие структуры решения. Рассмотрим это понятие и связанные с ним эффекты подробнее.

Если набор значений величин {a_ij, b_i c_j i=1,...,m; j=1,...,n} зафиксирован, то этому набору соответствует некоторый оптимальный план X=(x₁,x₂, …,x_n), назовем этот план базовым. Среди этих значений есть ряд ненулевых значений (т.е. эти виды продукции выпускать выгодно) и, возможно, часть нулевых (эти виды продукции выпускать не выгодно).

Обратим внимание, что понятия «выгодно-невыгодно» имеют смысл только при конкретном соотношении между нормами расхода при производстве, величинами прибыли и величинами запасов ресурсов. Нормы расхода при данной технологии, как правило, не меняются.

Сначала рассмотрим влияние изменения величины прибыли.

Для этого воспользуемся геометрической интерпретацией задачи ЛП. Поскольку изменение величины прибыли (коэффициентов целевой функции) не оказывает влияния на фазовые и естественные ограничения, многогранник допустимых решений не изменится. Малые изменения коэффициентов целевой функции приводят к небольшому повороту градиента и линий уровня относительно первоначального положения.

Положение вершины, соответствующей оптимальному плану, в которой линия уровня касается многогранника допустимых решений, также не изменится. Т.е. значение целевой функции изменится, но значения переменных, при которых этот оптимум достигается, не изменятся (рис.2.1).

Существенное изменение коэффициента целевой функции приводит к существенному повороту градиента (линии уровня), и оптимальное решение будет достигаться в другой точке многогранника допустимых решений.

Рис.2.1 Влияние изменения коэффициента целевой функции на положение точки оптимума

На рис.2.1 D - область допустимых решений;

- градиент, определяемый базовым набором коэффициентов; оптимальному положению соответствует вершина N и линия уровня ;

- градиент, соответствующий малому изменению базового набора коэффициентов; оптимальному положению соответствует та же (что и в базовом) вершина N и линия уровня ;

- градиент, соответствующий существенному изменению базового набора коэффициентов; оптимальному положению соответствует другая вершина M и линия уровня .

Из приведенных рассуждений следует, что оптимальное решение может измениться как при увеличении коэффициента С₁, так и при его уменьшении. Очевидно, что существует граница между несущественным уменьшением (когда вершина, соответствующая оптимальному плану, остается той же самой) и существенным уменьшением (когда вершина, соответствующая оптимальному плану, изменяется). Эта граница называется допустимым уменьшением и обозначается L₁ . Аналогично, существует граница между несущественным увеличением и существенным увеличением. Эта граница называется допустимым увеличением и обозначается U₁ .

Допустимое увеличение показывает, на сколько можно увеличить соответствующий коэффициент целевой функции (при условии постоянства остальных) без изменения оптимального плана. Аналогично, допустимое уменьшение показывает, на сколько можно уменьшить соответствующий коэффициент целевой функции (при условии постоянства остальных) без изменения оптимального плана.

Зная величины L₁ и U₁, можно построить интервал, в котором структура решения сохраняется. Нижняя граница этого интервала c₁ - L₁, верхняя граница c₁+U₁.

Эти рассуждения можно провести для каждого вида продукции и построить для них интервалы, в которых структура решения сохраняется.

Рассмотрим влияние изменения количества ресурса.

Геометрический смысл изменения количества ресурса заключается в том, что соответствующая граница многогранника допустимых решений перемещается параллельно сама себе (рис.2.2). Это приводит к тому, что координаты точки, соответствующей оптимальному плану, меняются. При небольших изменениях количества ресурса координаты точки, соответствующей оптимальному плану, определяются пересечением того же набора прямых (гиперплоскостей), что и в базовом решении. При значительных изменениях количества ресурса, координаты точки, соответствующей оптимальному плану, определяются пересечением других прямых (гиперплоскостей). Допустимое увеличение показывает, на сколько можно увеличить количество соответствующего ресурса (при условии постоянства остальных), без изменения набора прямых, определяющих координаты точки, соответствующей оптимальному плану. Аналогично, допустимое уменьшение показывает, на сколько можно уменьшить количество соответствующего ресурса (при условии постоянства остальных), без изменения набора прямых, определяющих координаты точки, соответствующей оптимальному плану.

Рис. 2.2. Влияние изменения количества ресурсов на положение точки оптимума

На рис.2.2 показаны Y₁,Y₂,Y₃ – прямые, соответствующие фазовым ограничениям;

D – область допустимых решений; определяется естественными и фазовыми ограничениями;

- градиент, определяемый набором коэффициентов целевой функции.

Случай I. Y ₁(b ₁ ) – базовое положение прямой, определяемое уравнением

(*),

при а ₁₂ ¹ 0; уравнение следует из ограничения а ₁₁ х ₁+ а ₁₂ х ₂£ b _1. Оптимальному плану соответствует вершина N, которая определяется как точка пересечения прямых Y ₁ и Y ₂. L (0) – соответствующая линия уровня.

На рис. 2.2А область допустимых решений обозначена одинарной и двойной штриховкой. Содержательно (в задаче распределения ресурсов) эта ситуация означает, что «узким местом» является количество ресурсов первого и второго вида, т.е. эти ресурсы закончатся в первую очередь. Другими словами, эти виды ресурсов будут лимитирующими.

Случай II. Малое изменение D b ₁ величины ресурса b ₁; Y ₁(b ₁₊D b ₁ ) – положение прямой, определяемое уравнением

(**),

при а ₁₂ ¹ 0. Это уравнение следует из ограничения , которое соответствует изменению величины ресурсов на D b ₁. Сравнивая уравнения (*) и (**), заключаем, что прямые параллельны (из равенства коэффициентов при х ₁). Оптимальному плану соответствует вершина N ₁, которая является точкой пересечения прямых Y ₁ и Y ₂. L (D b ₁) – соответствующая линия уровня.

На рис. 2.2А область допустимых решений обозначена двойной штриховкой. Эта ситуация соответствует тому, что «узким местом» по-прежнему остается количество ресурсов первого и второго вида.

Случай III. Существенное изменение D b ₂ величины ресурса b ₁; Y ₁(b ₁₊D b ₁ ) - положение прямой, определяемое уравнением

(***),

при а ₁₂ ¹ 0. Прямая Y ₁(b ₁₊D b ₂ ) параллельна прямым Y ₁(b ₁ ) и Y ₁(b ₁₊D b ₁ ). Сравнивая уравнения (*), (**) и (***), заключаем, что прямые параллельны (из равенства коэффициентов при х ₁).Оптимальному плану соответствует вершина N₂, которая является точкой пересечения прямых Y ₁ и Y ₃. L (D b ₂) – соответствующая линия уровня.

На рис. 2.2B область допустимых решений обозначена двойной штриховкой. Эта ситуация означает, что «узким местом» теперь становится количество ресурсов первого и третьего вида.

Из приведенных рассуждений следует, что лимитирующие виды ресурсов могут измениться как при увеличении коэффициента b₁, так и при его уменьшении. Очевидно, что существует граница между несущественным уменьшением и существенным уменьшением. Эта граница называется допустимым уменьшением и обозначается l₁ .

Аналогично, существует граница между несущественным увеличением и существенным увеличением. Эта граница называется допустимым увеличением и обозначается u_1.

Допустимое увеличение показывает, насколько можно увеличить количество ресурса первого вида b₁ (при условии постоянства остальных) без изменения лимитирующих видов ресурсов. Аналогично, допустимое уменьшение показывает, насколько можно уменьшить количество ресурса первого вида b₁ (при условии постоянства остальных) без изменения лимитирующих видов ресурсов.

Зная величины l₁ и u₁, можно построить интервал, в котором лимитирующие виды ресурсов сохраняются. Нижняя граница этого интервала: c₁ - l₁, верхняя граница: c₁+u₁.

Эти рассуждения можно провести для каждого вида ресурса и построить для них соответствующие интервалы.

 

Пример 6.

Строительное предприятие может возводить жилые объекты четырех типов: панельный, блочный, кирпичный и монолитный. Реализация единицы площади каждого вида жилья дает прибыль в 5; 7; 6 и 9,5 условных единиц соответственно. Перечень ресурсов, их количество и нормы расхода для производства единицы площади каждого вида жилья приведены в таблице 2.1. Требуется составить такой план строительства, чтобы прибыль от реализации была максимальной.

Решить задачу двумя способами: аналитически, используя симплекс-метод, и с помощью надстройки MS Excel «Поиск решения». При анализе результатов использовать отчеты, сформированные при работе надстройки MS Excel «Поиск решения».

Таблица 2.1

Исходные данные задачи распределения ресурсов

Вид ресурса	Нормы расхода	Количество ресурса в наличии
блочный	панельный	кирпичный	монолитный
электроэнергия
трудовые ресурсы
железобетонные изделия
кирпич
пиломатериалы

Решение

Составим математическую модель для данной задачи. Пусть x _j – количество выпускаемой продукции j -го типа, j=1,2,3,4. Как видно из таблицы 2.1, для выпуска одного квадратного метра блочного жилья требуется 1 единица электроэнергии, значит, для выпуска всего количества блочного жилья потребуется 1 x _j единиц электроэнергии, для строительства всего количества панельного жилья потребуется 3 x ₂ единиц электроэнергии и т.д. Таким образом, ограничение по электроэнергии будет иметь вид: 1 x ₁+3 x ₂+2 x ₃+1 x ₄£100. В этом ограничении левая часть показывает потребность в ресурсе (затраты электроэнергии на строительство жилья в объемах x ₁, x ₂, x ₃, x ₄), а правая – его имеющееся количество в наличии.

Аналогично можно составить ограничения для других ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь следующий вид:

	(2.7)
	(2.8)
	(2.9)

 

Задача может быть решена симплекс-методом, описанным выше. Сами симплекс-таблицы могут быть могут быть оформлены с использованием MS Excel. Возможный вариант оформления приведен на рис. 2.3. Решением задачи (2.7)-(2.9) является набор

x₁ =20, x₂ =0, x₃ =0, x₄ =20,

а значение целевой функции равно 290. Это означает, что выгодно производить продукцию первого и четвертого вида в количестве 20 единиц каждого, производить продукцию второго и третьего вида не выгодно. Суммарная величина прибыли при этом равна 290.

Заметим, что целевая функция после последней итерации будет иметь вид:

(2.10)

Коэффициенты 2 и 4, взятые с противоположным знаком, при 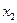и являются нормированной стоимостью продукции второго и третьего видов. Коэффициенты 4.5 и 0.1, взятые с противоположным знаком, при и являются теневой ценой ресурсов второго и четвертого видов.

Рис.2.3. Решение в MS Excel симплекс-методом

Рассмотрим решение задачи в MS Excel c помощью надстройки Поиск решения.

1. Разместим на рабочем листе MS Excel исходные данные, как показано на рис.2.4: в ячейках B3:E3 значения переменных можно положить равными 0, в ячейке F4 значение целевой функции вычисляется по формуле =СУММПРОИЗВ(B3:E3;B4:E4). Левая часть ограничений вычисляется следующим образом: в ячейку F7 заносится формула =СУММПРОИЗВ($B$3:$E$3;B7:E7), после чего она копируется в ячейки F8:F11.

Примечание: встроенная функция СУММПРОИЗВ(U,V), где U и V - интервалы ячеек, имеющих одинаковую конфигурацию, позволяет вычислить сумму произведений одноименных элементов. Результат вычисления по формуле СУММПРОИЗВ(B3:E3;B4:E4) равен В3*В4+С3*С4+D3*D4+E3*E4,

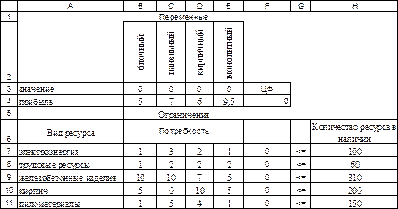т.е. этот результат соответствует значению ЦФ, определяемому формулой (2.7).

Рис.2.4. Исходные данные

2. Активизируем надстройку Поиск решения из пункта меню Сервис и заполним диалоговое окно, как это показано на рис.2.5 (в параметрах обязательно отметим линейность модели рис.2.6). Нажмем на кнопку Выполнить.

Рис.2.5. Диалоговое окно Поиск решения

3. На рис.2.7 показано полученное решение. При этом в ячейках диапазона B3:E3 находятся искомые значения объемов выпуска продукции, соответствующие оптимальному плану. В ячейке F4 находится значение целевой функции (ЦФ), которое соответствует этому оптимальному плану.

 

Рис.2.6. Параметры Поиска решения

 

 

Рис.2.7. Результаты работы «Поиска решения»

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: