Основана работа многих гидравлических устройств.

Гидравлический пресс (рис.1.21)состоит из двух цилиндров, соединенных между

Рис.1.20 Сообщающиеся сосуды собой трубопроводом. Цилиндры заполнены жидкостью. В малом цилиндре находится поршень (ныряло) диаметром d с рычагом, имеющим неподвижную опору. Плечи рычага b и (a-b). В большом цилиндре давление жидкости передается на поршень диаметром D. Если к рычагу приложена сила F, то силу давления Р₁, передаваемую на ныряло и создающую в жидкости дополнительное давление, можно определить из уравнения Р₁ b= Fа, откуда Р₁= Fа/ b.

Сила давления действующего на поршень большого цилиндра,

Р₂= Р₁ ω₂/ ω₁,

где ω₂ – площадь большого поршня (ω₂ = πD²/4);

ω₁ – площадь ныряла (ω₂₁= πd²/4).

Отсюда Р₂= Р₁(D/d)² = F .

С помощью подбора диаметров большого поршня и ныряла, а также плеч рычага можно получить сколь угодно большую силу Р₂ при значительно меньшей силе F. Усилие прессования Р_пр будет несколько меньше силы Р₂ из-за утечек жидкости и потерь на трение. Эти потери учитываются коэффициентом полезного действия пресса η, который на практике составляет 0,75…0,85:

Р_пр= η Р₂.

В современных прессах получают усилия прессования более 250000 кН.

 

Рис.1.21 Схема гидравлического пресса

 

Мультипликатор (рис.1.22)– устройство для повышения давления жидкости – состоит из двух связанных друг с другом цилиндров. В цилиндре низкого давления находится поршень большого диаметра D, который соединен с плунжером малого диаметра d, входящим в цилиндр высокого давления. Получаемое давление р_в будет в D²/d² раз больше подводимого давления р_н (на практике в 40-60 раз). Мультипликаторы, главным образом гидравлические, имеют ограниченное применение в современных гидравлических прессах (для увеличения усилия прессования), в пневмогидравлических усилителях (в многоточечных зажимных устройствах металлорежущих станков).

Ри..1.22 Схема гидрав­лического мультипли­катора:

1 — плунжер малого диа­метра; 2 — поршень боль­шого диаметра; 3 — рабо­чая жидкость

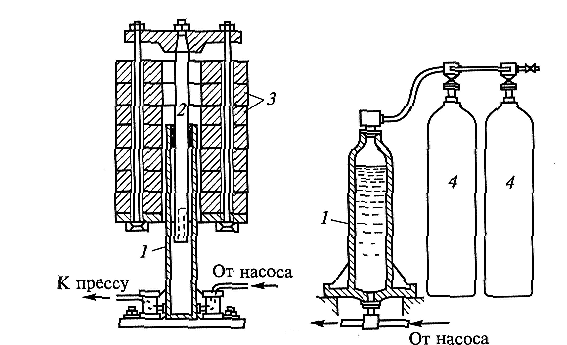Гидравлический аккумулятор (ри.1.23) служит для выравнивания давления и расхода жидкости или газа в гидравлических установках. Различают аккумуляторы поршневые и беспоршневые. Гидравлические аккумуляторы используют в системах с резко переменным расходом жидкости или газа. В периоды уменьшения потребления аккумулятор накапливает жидкость (газ), поступающую от насосов (или компрессоров), и отдает ее в моменты наибольших расходов.

Рис.1.23 Гидравлические аккумуляторы:

а — поршневой; 6 — беспоршневой;

/ — резервуар; 2— поршень;

3 — грузы; 4 — баллоны со сжатым воздухом

Поршневой аккумулятор имеет резервуар, как правило, цилиндрической формы, внутри которого свободно перемещается поршень. В резервуар подается жидкость под давлением, которое удерживается постоянным благодаря внешнему воздействию на поршень груза либо воздуха из подключенной пневмосети.

В беспоршневых аккумуляторах давление поддерживается постоянным за счет давления в пневмосети, непосредственно соединенной с резервуаром аккумулятора, причем давление воздуха равно давлению жидкости.

Разновидностью гидравлических аккумуляторов является пневматический аккумулятор для уменьшения колебаний давления сжатого воздуха в пневматической сети (применяют в крупных пневматических сетях, на ветроэлектростанциях и т.п.). Он представляет собой резервуар, включенный в воздуховод и снабженный предохранительным клапаном. Клапан регулирует на заданное предельное давление.

Домкрат (рис.1.24)– механизм для подъема тяжелых штучных грузов при выполнении ремонтных, монтажных или погрузочно-разгрузочных работ. Гидравлические домкраты могут быть периодического действия с ручным приводом и непрерывного действия с механическим приводом.

В домкрате периодического действия подъем поршня 1, являющегося опорой для груза, осуществляется рабочей жидкостью, подаваемой в нижнюю полость стакана 2 поршневым насосом, приводимым в действие вручную рукояткой 4 и снабженным всасывающим и нагнетательным клапанами. Опускание груза происходит при перепускании рабочей жидкости из стакана в резервуар насоса.

В домкратах непрерывного действия рабочая жидкость подается в надпоршневое пространство, в результате чего вверх перемещается не поршень, а стакан вместе с грузом, резервуаром и насосом. Стакан и поршень связаны между собой возвратными пружинами. Если при крайнем верхнем положении цилиндра под него подвести опоры и открыть спускной вентиль, то под действием усилия пружин поршень поднимается вверх и вытеснит жидкость в резервуар. Под поршень вновь подводят опоры, и цикл работы повторяется без перестановки домкрата. Гидравлические домкраты соединяют в себе достоинства винтовых и реечных. Они обладают высоким КПД (0,75…0,8), плавностью хода, точностью остановки, компактностью и большой грузоподъемностью. Их недостатки – малая скорость и небольшая высота подъема за один рабочий цикл.

Рис.1.24 Гидравлический домкрат периодического действия:

1 - поршень с подставкой для груза;
2 - стакан; 3 - клапанная коробка;.4 — рукоятка

ОСНОВЫ ГИДРОДИНАМИКИ

Основные понятия гидродинамики

 

Основные элементы движения жидкости. Причинами движения жидкости являются действующие на нее силы: объемные или массовые силы (сила тяжести, инерционные силы) и поверхностные силы (давление, трение). В отличие от гидростатики, где основной величиной, характеризующей состояние покоя жидкости, является гидростатическое давление, которое определяется только положением точки в пространстве, т.е. ,в гидродинамике основными элементами, характеризующими движение жидкости, будут два: гидродинамическое давление и скорость движения (течения) жидкости.

Гидродинамическое давление р – это внутреннее давление. развивающееся при движении жидкости. Скорость движения жидкости в данной точке и – это скорость перемещения находящейся в данной точке частицы жидкости, определяемая длиной пути l, пройденного этой частицей за единицу времени t.

В общем случае основные элементы движения жидкости р и и для данной точки зависят от ее положения в пространстве (координат точки) и могут изменяться во времени. Аналитически это положение гидродинамики записывается так:

,

.

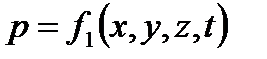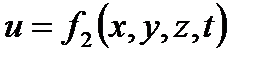Задачей гидродинамики и является определение основных элементов движения жидкости р и u, установление взаимосвязи между ними и законов изменения их при различных случаях движения жидкости.

Траектория частицы.Если в массе движущейся жидкости взять какую-либо частицу жидкости и проследить ее путь за какой-то промежуток времени (конечный, достаточно большой), то можно получить некоторую линию, выражающую геометрическое место этой точки в пространстве за время .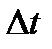

рис. 2.1

Линия тока. Если в массе движущейся жидкости в данный момент времени t взять какую-либо точку 1(рис.2.1), то можно в этой точке построить вектор скорости и₁, выражающий величину и направление скорости движения частицы жидкости в данной точке 1в этот момент времени.

В тот же момент времени t можно взять и другие точки в движущейся жидкости, например, точки 2, 3, 4,...... в которых также можно построить векторы скоростей u ₂, u ₃, и₄,… выражающие скорость движения других частиц жидкости в тот же момент.

Можно выбрать точки 1, 2, 3, 4... и провести через них плавную кривую, к которой векторы скоростей будут всюду касательны. Эта линия и называется линией тока.

Таким образом, линией тока называется линия, проведенная через ряд точек в движущейся жидкости так, что в данный момент времени векторы скорости частиц жидкости, находящихся в этих точках, направлены по касательной к этой линии. В отличие от траектории, которая показывает путь движения одной частицы жидкости за определенный промежуток времени , линия тока соединяет разные частицы и дает некоторую мгновенную характеристику движущейся жидкости в момент времени t. Через заданную точку в данный момент времени можно провести только одну линию тока.

Если в данных точках движущейся жидкости величина и направление скорости и гидродинамическое давление с течением времени не изменяются (такое движение называется установившимся), то и линия тока, и траектория частицы, оказавшейся на ней, совпадают и со временем не изменяются. В этом случае траектории частиц являются и линиями тока.

Рис. 2.2

Элементарная струйка. Если в движущейся жидкости выделить весьма малую элементарную площадку , перпендикулярную направлению течения, и по контуру ее провести линии тока, то полученная поверхность называется трубкой тока, а совокупность линий тока, проходящих сплошь через площадку 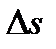, образует так называемую элементарную струйку (рис.2.2).

Элементарная струйка характеризует состояние движения жидкости в данный момент времени t. При установившемся движении элементарная струйка имеет следующие свойства:

1. форма и положение элементарной струйки с течением времени остаются неизменными, так как не изменяются линии тока;

2. приток жидкости в элементарную струйку и отток из нее через боковую поверхность невозможен, так как по контуру элементарной струйки скорости направлены по касательной;

3. скорость и гидродинамическое давление во всех точках поперечного лечения элементарной струйки можно считать одинаковым ввиду малости площади .

Поток. Совокупность элементарных струек движущейся жидкости, проходящих через площадку достаточно больших размеров, называется потоком жидкости. Поток ограничен твердыми поверхностями, по которым происходит движение жидкости (труба), и атмосферой (река, лоток, канал и т.п.).

 

 

2.2 Понятие о потоке жидкости.

 

Гидравлические элементы потока. Живым сечением называется поверхность в пределах потока, проведенная перпендикулярно к линиям тока (элементарным струйкам). В общем случае эта поверхность криволинейная (на рис.2.3 поверхность ABC). Однако в большинстве случаев практической гидравлики поток жидкости можно представить параллельно-струйным или с очень малым углом расхождения струек, а за живое сечение принять плоское поперечное сечение потока (на рис. 2.3 плоскость АС). Площадь живого сечения обозначается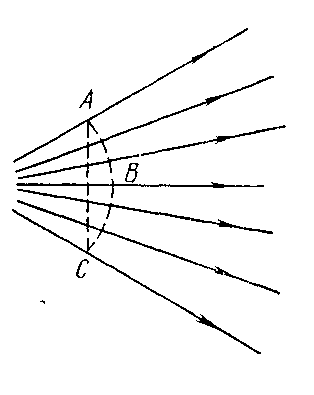

Рис.2.3

буквой s.

Смоченным периметром называется длина части периметра живого сечения, в пределах которой поток соприкасается с твердыми внешними стенками. Смоченный периметр обозначают буквой П.

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру:

.

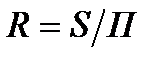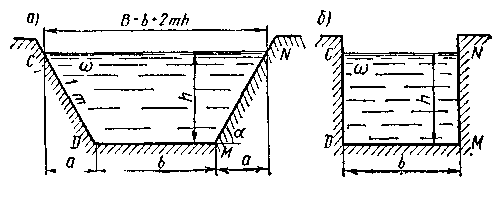
На рис. 2.4 приведены примеры поперечных сечений потока:

а) трапецеидальное; б) прямоугольное; в) круговое.

Для кругового сечения, заполненного жидкостью полностью (рис.2.4, в): ; ; .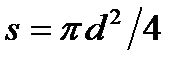

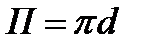Расход жидкости и средняя скорость. Расходом жидкости называется количество жидкости, проходящей через данное живое сечение потока в единицу времени.

Расход потока жидкости обозначают Q, а элементарной струйки – 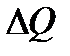. Единицами измерения расхода являются: м³/сек, м³/ч или л/сек, л/ч и др.

Рис. 2.4

Рассмотрим элементарную струйку (рис.2.2) с поперечным сечением и постоянной скоростью движения частицы жидкости и. Через промежуток времени t частицы переместятся из сечения 1-1 в сечение 2-2 на расстояние l. При этом через сечение 1-1 пройдет элементарный объем жидкости 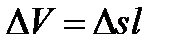. Разделив обе части уравнения на t, получим

,

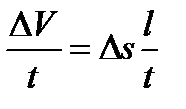но –расход элементарной струйки (объем, прошедший через элемент живого сечения 1-1 в единицу времени); –скорость движения частиц жидкости (путь, пройденный частицами жидкости за единицу времени).

Отсюда

рис.2.5

,

т. е. расход элементарной струйки равен площади ее поперечного сечения, умноженной на скорость в этом сечении. Поток жидкости в данном живом сечении представляет совокупность (сумму) большого числа элементарных струек, заполняющих сплошь площадь живого сечения, поэтому для определения расхода потока через живое сечение s необходимо взять сумму расходов 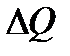элементарных струек, т.е.

. (*)

В общем случае, чтобы воспользоваться формулой (*) для определения расхода потока, надо знать закон распределения скоростей по живому сечению, который очень сложен или вообще неизвестен. Поэтому для практических расчетов вводится понятие средней скорости потока.

На рис.2.5 представлен график (эпюра) распределения действительных скоростей в точках живого сечения потока, из которого видно, что скорости по сечению распределяются неравномерно. При действительных скоростях через живое сечение проходит определенный расход Q. Можно найти некоторую постоянную для всех точек сечения фиктивную скорость, при которой через данное сечение проходил бы тот же самый расход, что и при действительных скоростях движения жидкости. Эта скорость v будет средней из действительных скоростей. Подставляя в формулу (*) скорость v получим 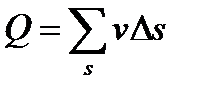, но 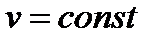, ,поэтому , (**)

т. е. расход жидкости в данном сечении потока равен произведению средней скорости движения жидкости, умноженной на площадь живого сечения.

Итак, средней скоростью потока в данном сечении v называется такая одинаковая для всех точек живого сечения скорость движения жидкости, при которой через это живое сечение проходит тот же расход Q, что и при действительных скоростях движения жидкости и.

Из формулы (**) можно написать

,

.

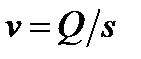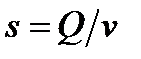Эти формулы используются при решении основных гидравлических задач, связанных с потоком жидкости.

 

Виды движения жидкости

 

Установившимся стационарным движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р не изменяются с течением времени, т.е. зависят только от координат точки. Аналитически это условие запишется так:

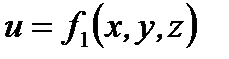и .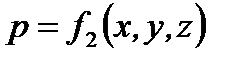

Неустановившимся (нестационарным) движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р – постоянно изменяются, т.е. зависят не только от положения точки в пространстве, но и от времени . Аналитически это условие запишется так:

и .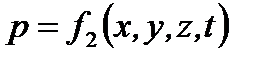

Примером установившегося движения может быть: движение жидкости в канале, в реке при неизменных глубинах, истечение жидкости из резервуара при постоянном уровне жидкости в нем и др. Неустановившееся движение – это движение жидкости в канале или реке при переменном уровне или при опорожнении резервуара, когда уровень жидкости в нем непрерывно изменяется.

В дальнейшем будет изучаться главным образом установившееся движение жидкости и в отдельных случаях будут разбираться примеры неустановившегося движения.

Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.

Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае 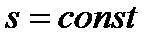; средние скорости по длине потока также не изменяются, т.е. 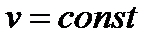. Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.

Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).

Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.

Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.

Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.

Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.

Отметим следующие свойства потока при плавно изменяющемся движении:

1. поперечные сечения потока плоские, нормальные к оси потока;

2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;

3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: