 |
Случайные события. Вероятность
|
|
|
|
ВЕРОЯТНОСТНЫЕ МОДЕЛИ В ЗАДАЧАХ
ТЕОРИИ ИНФОРМАЦИИ
Случайные события. Вероятность
Событие - всякий факт, который в результате опыта может произойти или не произойти. Вероятность события - это число, которое является мерой возможности реализации события. Вероятность P(A) случайного события A заключена в пределах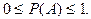 
Достоверное событие U такое, что 
Невозможное событие V такое, что 
Суммой или объединением событий называется событие A, которое происходит тогда и только тогда, когда происходит, по крайней мере, одно из этих событий. Сумма обозначается
Произведением или пересечением событий 
называется такое событие A, которое происходит тогда и только тогда, когда происходят события вместе. Произведение обозначается
События образуют полную группу событий, если в результате опыта появляется хотя бы одно из них:
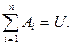
События A и B называются несовместными, если их совместное появление невозможно: 
Два события называются противоположными, если они несовместны и образуют полную группу. Событие, противоположное событию A, обозначается 
.
Когда рассматриваемый опыт имеет N равновозможных исходов, которые несовместны и составляют полную группу, вероятность события А можно рассчитать по формуле:
где m - число исходов, которые приводят к наступлению события A.
Частотой или статистической вероятностью P*(A) события A в данной серии испытаний называется отношение числа опытов n, в которых появилось событие, к общему числу N произведенных опытов:
По теореме Бернулли при большом числе опытов частота сходится по вероятности к вероятности события.
Расчеты вероятности сложного события A через вероятности более простых событий базируются на использовании основных теорем теории вероятностей.
|
|
|
Теорема сложения вероятностей. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:
Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое имело место:
где 
- условная вероятность события B, т.е. вероятность события B, вычисленная в предположении, что имело место событие A.
Во многих ситуациях событие A может появиться лишь как случайное следствие одного из несовместных событий 
образующих полную группу. В этих случаях безусловная вероятность P(A) события A при известных вероятностях 
и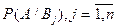 
определяется по формуле полной вероятности:
При этих же данных можно найти значения вероятностей событий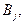 
если предположить, что событие A уже произошло. Задачи такого типа решаются с помощью формулы Байеса:
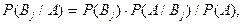
Рассмотрим несколько примеров.
Пример 1. В последовательности из N двоичных символов имеется M единиц. При передаче данной последовательности сохраняется n символов, остальные теряются. Какова вероятность того, что среди них будет не более m единиц?
Решение. Пусть A - событие, состоящее в том, что среди двоичных символов будет не более m единиц. Событие A произойдет тогда, когда среди n двоичных символов не будет ни одной единицы (событие 
) или одна единица (событие 
), или две (событие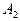 
),..., или окажется m единиц (событие 
), т.е.
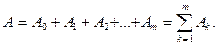
Вероятность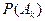 
события 
можно рассчитать следующим образом. Общее число возможных выборов n символов из N равно числу сочетаний из N по n, т.е. 
. Благоприятствующими событию являются случаи, когда из общего числа M единиц сохранено ровно K, что возможно в 
случаях. На каждый из этих случаев в сохраненной последовательности символов может быть 
различных комбинаций (
) нулей. Общее число случаев, благоприятствующих событию , равно 
. Поэтому
|
|
|
По теореме сложения
Пример 2. По каналу связи с помехами передается одна из двух команд управления управления в виде кодовых комбинаций 11111 и 00000, вероятности передачи этих команд равны соответственно 0,7 и 0,3. Вероятность правильного приема каждого из символов 0 и 1 равна 0,6. Символы искажаются помехами независимо друг от друга. На выходе канала имеем кодовую комбинацию 10110. Оценить, какая команда была передана.
Решение. Пусть A - событие, состоящее в приеме комбинации 10110. Это событие может произойти только в совокупности с одним из событий: 
- передавалась команда 11111, 
- передавалась команда 00000. При этом 
Условная вероятность приема комбинации 10110 при условии, что передавалась команда 11111 равна
Аналогично 
По формуле Байеса
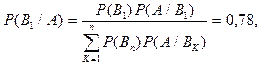
Сравнивая найденные результаты, заключаем, что более вероятна передача команды 11111.
|
|
|
