 |
Дискретная и непрерывная случайные величины
|
|
|
|
Случайной величиной называется такая переменная величина, которая в результате опыта может принимать то или иное заранее неизвестное значение  , из известного множества значений
, из известного множества значений  . Различают два основных типа случайных величин: дискретные и непрерывные.
. Различают два основных типа случайных величин: дискретные и непрерывные.
Дискретная случайная величина может принимать конечное или бесконечное множество значений 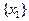 , которые можно пронумеровать
, которые можно пронумеровать 
Полной статистической характеристикой случайной величины является закон распределения вероятностей. В случае дискретной величины  под ним понимается соотношение, устанавливающее зависимость между возможными значениями дискретной случайной величины и их вероятностями
под ним понимается соотношение, устанавливающее зависимость между возможными значениями дискретной случайной величины и их вероятностями  при этом
при этом 
Закон распределения дискретной случайной величины можно задать в различных формах: табличной, графической, аналитической. Универсальной характеристикой, одинаково пригодной для дискретных и для непрерывных одномерных случайных величин, является функция распределения вероятностей 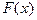 (интегральная функция распределения), определяющая вероятность
(интегральная функция распределения), определяющая вероятность  того, что случайная величина
того, что случайная величина  примет значение меньше некоторого некоторого числа
примет значение меньше некоторого некоторого числа 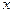 :
:
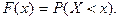
Функция распределения обладает следующими свойствами:
1. 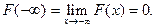
2. 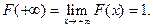
3.  неубывающая функция, т.е.
неубывающая функция, т.е.  при
при 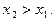
4. 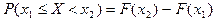 .
.
Функция распределения дискретной случайной величины представляет собой ступенчатую функцию со скачками в точках 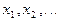
Во многих ситуациях невозможно определить закон распределения случайной величины, часто в этом нет необходимости. В таких ситуациях рассматривают отдельные параметры (числовые характеристики) этого закона. Наиболее важными числовыми характеристиками случайной величины  с множеством значений
с множеством значений  и законом распределения вероятностей
и законом распределения вероятностей 
|
|
|
являются:
 - математическое ожидание;
- математическое ожидание;
 - средний квадрат;
- средний квадрат;
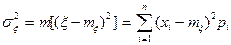 - дисперсия.
- дисперсия.
Возможные значения непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток или даже всю ось. Функция распределения непрерывной случайной величины представляет собой непрерывную функцию.
Часто предполагают, что функции распределения непрерывных случайных величин дифференцируемы во всей области возможных значений случайных величин. При таком предположении непрерывная случайная величина  чаще своего описывается плотностью распределения вероятности
чаще своего описывается плотностью распределения вероятности  , которая иногда называется дифференциальным законом распределения или дифференциальной функцией распределения. Плотность вероятности определяется как производная функции распределения:
, которая иногда называется дифференциальным законом распределения или дифференциальной функцией распределения. Плотность вероятности определяется как производная функции распределения:

Плотность вероятности обладает следующими основными свойствами:
1. Плотность вероятности неотрицательна, т.е. 
2. Вероятность попадания непрерывной случайной величины в интервал  равна интегралу от плотности вероятности в этих пределах:
равна интегралу от плотности вероятности в этих пределах:
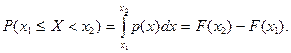
3. Интеграл в бесконечных пределах от функции  равен единице (условие нормировки):
равен единице (условие нормировки):
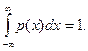
Для непрерывной случайной величины формулы для математического ожидания и дисперсии имеют вид:

Рассмотрим несколько примеров.
Пример 1. По двоичному каналу связи с помехами передаются две цифры 1 и 0 с вероятностями  Вероятность перехода единицы в единицу и нуля в нуль соответственно равны
Вероятность перехода единицы в единицу и нуля в нуль соответственно равны  ,
, 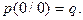 Определить закон распределения вероятностей случайной величины
Определить закон распределения вероятностей случайной величины  - однозначного числа, получаемого на приемной стороне.
- однозначного числа, получаемого на приемной стороне.
Решение.  . Нуль
. Нуль  на приемной стороне может быть получен в двух случаях: при передаче нуля или при передаче единицы, следовательно, по формуле полной вероятности
на приемной стороне может быть получен в двух случаях: при передаче нуля или при передаче единицы, следовательно, по формуле полной вероятности


Поэтому 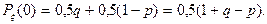
Аналогично 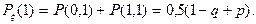
Распределение вероятностей представлено в табл. 1.
| Табл. 1. | |||||
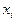
| |||||
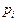
| 
| 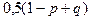
| |||
Пример 2. Производится прием символов 0 и 1 до первого появления символа 1. Вероятность появления 1 при приеме  . Принимается не более четырех символов. Вычислить математическое ожидание
. Принимается не более четырех символов. Вычислить математическое ожидание  , дисперсию
, дисперсию  и среднеквадратическое отклонение
и среднеквадратическое отклонение  величины числа принятых символов.
величины числа принятых символов.
|
|
|
Решение. Распределение вероятностей можно рассчитать следующим образом:

По определению математического ожидания имеем:
 ,
,
для дисперсии получаем:
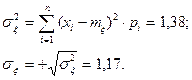
Пример 3. Функция распределения 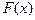 случайной величины
случайной величины  задана графиком (рис. 1.1).
задана графиком (рис. 1.1).
   

         F(x) F(x)
| Требуется:
1) найти аналитическое выражение для функции
распределения;
2) построить график плотности вероятности  3) определить вероятность
3) определить вероятность  того, что величина того, что величина  примет значение от 3,5 до 4,5.
Решение.1. Когда значения величины
примет значение от 3,5 до 4,5.
Решение.1. Когда значения величины  заключе
ны в пределах от 3 до 5, функция распределения заключе
ны в пределах от 3 до 5, функция распределения
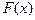 представляет собой отрезок прямой, прохо- представляет собой отрезок прямой, прохо-
|
дящей через две точки с координатами (3,0) и (5,1). Используя уравнение прямой в виде  получаем
получаем  т.е.
т.е.  Следовательно,
Следовательно,
 при
при 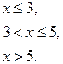
2. По определению,  Поэтому
Поэтому
    
         при при 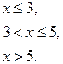
3. | p(x) |
Задачи
1.3.1. Сообщения  источника, заданного распределением вероятностей
источника, заданного распределением вероятностей  , кодируются словами:
, кодируются словами: 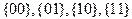 соответственно. Необходимо найти вероятность появления единицы в первой позиции кодового слова при условии, что во второй позиции кодового слова появилась единица; вероятность появления нуля во второй позиции кодового слова при условии, что в первой позиции кодового слова появился нуль; вероятность появления сообщения
соответственно. Необходимо найти вероятность появления единицы в первой позиции кодового слова при условии, что во второй позиции кодового слова появилась единица; вероятность появления нуля во второй позиции кодового слова при условии, что в первой позиции кодового слова появился нуль; вероятность появления сообщения  при условии, что в первой позиции кодового слова появился нуль. Исходные данные:
при условии, что в первой позиции кодового слова появился нуль. Исходные данные:

1.3.2. Сигнал  подается на вход канала с вероятностью
подается на вход канала с вероятностью  Поступивший сигнал воспроизводится на выходе с вероятностью
Поступивший сигнал воспроизводится на выходе с вероятностью  и теряется с вероятностью
и теряется с вероятностью  При отсутствии сигнала на входе возможен ложный сигнал на выходе с вероятностью
При отсутствии сигнала на входе возможен ложный сигнал на выходе с вероятностью 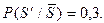 Какова вероятность правильного решения, если мы по сигналу на выходе считаем, что был сигнал на входе? Какова вероятность ошибки в этом случае? Какова вероятность правильного решения, если мы при отсутствии сигнала на выходе, считаем, что на входе его нет? Какова при этом вероятность ошибки?
Какова вероятность правильного решения, если мы по сигналу на выходе считаем, что был сигнал на входе? Какова вероятность ошибки в этом случае? Какова вероятность правильного решения, если мы при отсутствии сигнала на выходе, считаем, что на входе его нет? Какова при этом вероятность ошибки?
|
|
|
1.3.3. По двоичной системе связи с помехами передается одна из двух команд в виде двоичных векторов  или
или  Вероятность правильной передачи каждой координаты в системе равна
Вероятность правильной передачи каждой координаты в системе равна 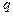 , причем координаты искажаются независимо друг от друга. На выходе зарегистрирована кодовая комбинация
, причем координаты искажаются независимо друг от друга. На выходе зарегистрирована кодовая комбинация 

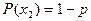 . Определить правило решения о предпочтении команды
. Определить правило решения о предпочтении команды  или
или  в виде соотношений p и q. Определить, какая команда передавалась для p= 0,5+0,01 N; q= 0,7+0,01 N.
в виде соотношений p и q. Определить, какая команда передавалась для p= 0,5+0,01 N; q= 0,7+0,01 N.
1.3.4. Некоторый объект наблюдается с помощью двух станций слежения.
Известно, что объект может находиться в двух состояниях  и
и  , случайно переходя из одного в другое. Априори известно, что (50- А)% времени объект может находиться в состоянии
, случайно переходя из одного в другое. Априори известно, что (50- А)% времени объект может находиться в состоянии  , а (50+ А)% времени - в состоянии
, а (50+ А)% времени - в состоянии  . Станция слежения №1 передает ошибочные сведения о состоянии объекта в двух процентах случаев, а станция №2 - в восьми процентах. В некоторый момент времени станция №1 приняла решение
. Станция слежения №1 передает ошибочные сведения о состоянии объекта в двух процентах случаев, а станция №2 - в восьми процентах. В некоторый момент времени станция №1 приняла решение  состоящее в том, что объект находится в состоянии
состоящее в том, что объект находится в состоянии  , а станция №2 - решение
, а станция №2 - решение 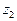 , что объект находится в состоянии
, что объект находится в состоянии 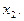 Определить, какое из решений
Определить, какое из решений  или
или 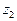 является более достоверным при
является более достоверным при 
1.3.5. В двоичной системе связи под воздействием шума каждый из входных символов изменяет независимым образом свое значение с вероятностью 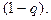 Четыре статистически независимых сообщения могут передаваться по системе с одинаковой вероятностью в виде кодовых векторов
Четыре статистически независимых сообщения могут передаваться по системе с одинаковой вероятностью в виде кодовых векторов 
 На выходе регистрируются сигналы:
На выходе регистрируются сигналы: 
 Определить распределение вероятностей входного алфавита
Определить распределение вероятностей входного алфавита  и входного алфавита
и входного алфавита 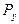 .
.
1.3.6. Определить распределение вероятностей входных и выходных сигналов системы. Дана матрица системы передачи информации
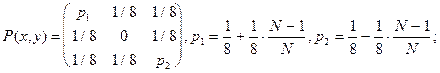
1.3.7. Принимается последовательность из  двоичных символов. Символы поступают независимо. Вероятность появления единицы при приеме
двоичных символов. Символы поступают независимо. Вероятность появления единицы при приеме 
Определить среднее число единиц в последовательности. Какова дисперсия числа единиц в последовательности?
1.3.8. Полезный сигнал на входе канала связи имеет постоянное значение 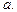 В канале присутствует помеха с нулевым математическим ожиданием
В канале присутствует помеха с нулевым математическим ожиданием 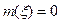 и дисперсией
и дисперсией  На выходе канала значение принимаемого сигнала
На выходе канала значение принимаемого сигнала 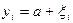 фиксируется
фиксируется  раз. В качестве оценки
раз. В качестве оценки  входного сигнала принимается среднее арифметическое зафиксированных значений выходного сигнала
входного сигнала принимается среднее арифметическое зафиксированных значений выходного сигнала 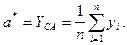 Определить математическое ожидание оценки и среднеквадратичное отклонение оценки
Определить математическое ожидание оценки и среднеквадратичное отклонение оценки  от истинного значения
от истинного значения  находилась в пределах 0,1.
находилась в пределах 0,1.
|
|
|
1.3.9. Плотность вероятности 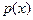 случайной величины
случайной величины  имеет вид
имеет вид

где  и
и  - постоянные величины. Найти соотношение, которому должны удовлетворять постоянные
- постоянные величины. Найти соотношение, которому должны удовлетворять постоянные  и
и  . Вычислить функцию распределения
. Вычислить функцию распределения 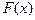 случайной величины
случайной величины  . Построить графики плотности вероятности
. Построить графики плотности вероятности 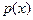 и функции распределения
и функции распределения 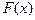 при
при  =2.
=2.
1.4. Контрольные вопросы
1.4.1. Что такое случайное событие? Определите события: достоверное, невозможное, противоположное, сумма событий, произведение событий, полная группа событий.
1.4.2. Что такое вероятность?
1.4.3. Что такое условная вероятность? Каковы ее свойства?
1.4.4. Сформулируйте теорему умножения вероятностей.
1.4.5. Сформулируйте теорему сложения вероятностей.
1.4.6. Напишите формулу полной вероятности.
1.4.7. Напишите формулу Байеса.
1.4.8. Известны события A,B,C, причем A влечет за собой B. Определить: AB, A+B, ABC, A+B+C.
1.4.9. Система состоит из четырех приемников с непересекающимися сферами. Длительность сигнала такова, что он не может быть одновременно обнаружен двумя приемниками. Найти связь событий: A - сигнал обнаружен системой,  - сигнал обнаружен i -м приемником.
- сигнал обнаружен i -м приемником.
1.4.10. Прибор состоит из двух блоков первого типа и трех блоков второго типа. Определены события: 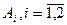 - исправен i -й блок первого типа;
- исправен i -й блок первого типа; 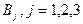 - исправен j -й блок второго типа. Прибор исправен, если работает хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие «Прибор работает» через события
- исправен j -й блок второго типа. Прибор исправен, если работает хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие «Прибор работает» через события  и
и  .
.
1.4.11. Что является полным описанием дискретной случайной величины?
1.4.12. Что такое математическое ожидание, дисперсия, средний квадрат дискретной величины?
1.4.13. Показать, что математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий этих величин.
1.4.14. Показать, что математическое ожидание произведения независимых случайных величин равно произведению матожиданий этих величин.
1.4.15. Доказать, что дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.
1.4.16. Вывести расчетное соотношение для дисперсии 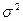 через матожидание
через матожидание  и средний квадрат
и средний квадрат 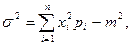 где
где 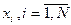 - возможные значения случайной величины;
- возможные значения случайной величины; 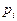 - вероятность этих значений.
- вероятность этих значений.
1.4.17. Показать, что для среднеарифметического независимых случайных величин  с одинаковыми средними
с одинаковыми средними  и дисперсиями
и дисперсиями 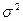 выполняются соотношения
выполняются соотношения 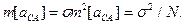
1.4.18. Как определяется плотность распределения вероятности непрерывной случайной величины?
|
|
|
1.4.19. Какими свойствами обладает плотность распределения вероятности непрерывной случайной величины?
1.4.20. Что такое математическое ожидание, дисперсия непрерывной случайной величины?
|
|
|



 График плотности вероятности
График плотности вероятности 