 |
Информационная мера шеннона.
|
|
|
|
Количество информации и избыточность.
Дискретные системы связи - системы, в которых как реализации сообщения, так и реализации сигнала представляют собой последовательности символов алфавита, содержащего конечное число элементарных символов.
Пусть 
и 
- случайные величины с множествами возможных значений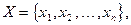 
Количество информации 
при наблюдении случайной величины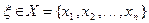 
с распределением вероятностей 
задается формулой Шеннона:
Единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения.
При равномерном распределении 
количество информации задается формулой Хартли:
.
Справедливы следующие соотношения:
1) 
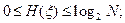
2) 
3) 
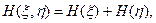если и - независимы.
Избыточностью называется 
Рассмотрим примеры.
Пример 1. Имеются два источника информации, алфавиты и распределения вероятностей которых заданы матрицами:
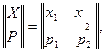
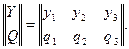
Определить, какой источник дает большее количество информации, если
1) 
2) 
Решение. Для первого источника при равновероятном распределении воспользуемся формулой Хартли. Для 
и 
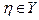имеем
Следовательно, источник с тремя символами дает большее количество информации. Для второго случая воспользуемся формулой Шеннона:
с учетом условия задачи имеем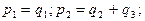 
С другой стороны,
Поскольку
то 
Пример 2. Источник сообщений выдает символы из алфавита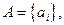 
с вероятностями 
Найти количество информации и избыточность.
Решение. По формуле Шеннона
(бит).
По определению избыточности 
Энтропия непрерывных сообщений
Непрерывныесистемы передачи информации - системы, в которых как реализации сообщения, так и реализации сигнала на конечном временном интервале 
представляют собой некоторые непрерывные функции времени.
|
|
|
Пусть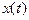 
- реализации непрерывного сообщения на входе какого-либо блока схемы связи, 
- реализация выходного сообщения (сигнала), 
- плотность вероятности ансамбля входных сообщений, 
- плотность вероятности ансамбля выходных сообщений
Формулы для энтропии 
непрерывных сообщений получаются путем обобщения формул для энтропии дискретных сообщений. Если 
- интервал квантования (точность измерения), то при достаточно малом энтропия непрерывных сообщений
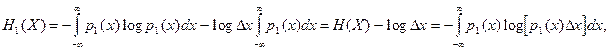
где 
По аналогии 
Пример 1. По линии связи передаются непрерывные амплитудно-модулированные сигналы 
распределенные по нормальному закону с математическим ожиданием 
и дисперсией 
Определить энтропию 
сигнала при точности его измерения 
Решение. По условию плотность вероятности сигнала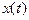
Подставляя числовые значения, получаем
дв. ед.
Задачи
2.3.1. Определить энтропию источника информации 
, передающего сообщения 
, 
Вероятность сообщений определяются по формулам:
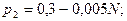
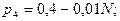
Известно, что в сообщении источника 100 символов. Определить, сколько символов потребуется для передачи этой информации при использовании безызбыточного алфавита той же размерности;
2.3.2. На выходе источника сообщений может появляться нуль и единица. Вероятность появления каждого сообщения изменяется со временем и в каждый момент времени может быть определена по формулам:
Необходимо исследовать изменение энтропии источника информации во времени и определить момент времени, когда математическая модель опыта теряет смысл. Энтропия источника сообщений вычисляется в соответствии с формулой Шеннона. Все вычисления сводятся в таблицу:
| Таблица 2 | |||||||
| t | P(0) | P(1) | H(0) | H(1) | H | ||
|
|
|
Значения 
задаются целыми числами через равные промежутки времени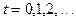 
Математическая модель опыта имеет смысл, когда выполняются соотношения для вероятностей 
Значения , при котором эти соотношения перестают выполняться, и есть момент времени, когда модель опыта теряет смысл.
После заполнения таблицы результатами вычислений следует построить графики изменения 
При анализе графиков обратить внимание на точку, где энтропия принимает наибольшее значение и наименьшее значение. Указать значения вероятностей появления символов в этих точках и моменты времени.
2.3.3. Определить значение энтропии 
по заданным аналитическим выражениям плотности вероятности 
:
1) для равномерного (прямоугольного) закона распределения:
,
2) для Гауссовского (нормального) закона распределения:
,
3) для Симпсоновского (треугольного) закона распределения:
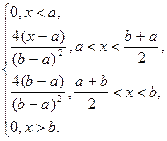
2.4. Контрольные вопросы
2.4.1. Дать определение энтропии.
2.4.2. Как связаны между собой формулы Хартли и Шеннона?
2.4.3. Может ли энтропия быть отрицательной?
2.4.4. В каких случаях энтропия равна нулю?
2.4.5. При каких условиях энтропия принимает максимальное значение?
2.4.6. В чем состоит правило сложения энтропий для независимых источников?
2.4.7. Что понимают под непрерывными системами передачи?
2.4.8. Как определить количество информации непрерывных сообщений?
|
|
|
