 |
Абсолютная и относительная погрешности
|
|
|
|
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
По проведению практических занятий
По дисциплине
«ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
по направлению
010300.68 Математическое обеспечение и администрирование информационных систем
Тольятти 2015
Содержание
1 Планы практических занятий. 3
1.1 Занятие № 1. Теория погрешности. 3
1.2 Занятие № 2. Решения алгебраических уравнений. Отделение корней. 11
1.3 Занятие № 3. Метод хорд (секущих) и метод деления пополам. 13
1.4 Занятие № 4. Метод Ньютона (касательных). 17
1.5 Занятие № 5. Комбинированный метод. 20
1.6 Занятие № 6. Метод итераций. 21
1.7 Занятие № 7. Прямые методы решения систем линейных алгебраических уравнений. 24
1.8 Занятие № 8. Метод итераций для систем уравнений. 29
1.9 Занятие № 9. Равномерное приближение функций многочленами. Интерполяционный многочлен Лагранжа. 35
1.10 Занятие № 10. Интерполяционный многочлен Ньютона. Многочлены Чебышева. 44
1.11 Занятие № 11. Интерполяция с кратными узлами и формула Эрмита. 65
1.12 Занятие № 12. Понятие сплайна. Виды сплайнов. 69
1.13 Занятие № 13. Численное дифференцирование. 76
1.14 Занятие № 14. Численное интегрирование. Квадратурные формулы Ньютона-Котеса. 79
1.15 Занятие № 15. Квадратурные формулы Гаусса. 88
1.16 Занятие № 16. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Классификация методов. Метод Пикара. 93
1.17 Занятие № 17. Методы Эйлера. 96
1.18 Занятие № 18. Методы Рунге-Кутта. 105
1.19 Занятие № 19. Пошаговый контроль точности. Метод Кутты-Мерсона. 110
1.20 Занятие № 20. Многошаговые методы Адамса. 114
1.21 Занятие № 21. Методы прогноза и коррекции. 119
1.22 Занятие № 22. Метод Милна четвертого порядка. 122
Приложение 1. 126
Приложение 2. 128
|
|
|
Индивидуальное домашнее задание № 1. 129
Индивидуальное задание №2. 134
Индивидуальное задание №3. 139
Индивидуальное домашнее задание № 4. 143
Литература. 147
Планы практических занятий
Занятие № 1. Теория погрешности.
Источники и виды погрешности
На некоторых этапах решения задачи на ЭВМ могут возникать погрешности, искажающие результаты вычислений. Оценка степени достоверности получаемых результатов является важнейшим вопросом при организации вычислительных работ. Это особенно важно при отсутствии опытных или других данных для проверки адекватности модели.
Погрешность решения задачи обуславливается следующими причинами:
1.Математическое описание задачи является неточным, в частности, неточно заданы исходные данные.
2.Применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, и, поэтому вместо получения точного решения задачи приходится прибегать к приближенному.
3.При вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления. Погрешности, соответствующие этим причинам, называют:
1) неустранимой погрешностью,
2) погрешностью метода,
3) вычислительной погрешностью.
Часто неустранимую погрешность разделяют на две части:
а) неустранимой погрешностью называют лишь погрешность, являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи;
в) погрешность, являющуюся следствием несоответствия математического описания задачи реальности, называют погрешностью математической модели.
Математическая модель, принятая для описания данного процесса или явления, может внести существенные погрешности, если в ней не учтены какие-либо существенные черты рассматриваемой задачи. В частности, математическая модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других; поэтому важно правильно учитывать область её применимости.
|
|
|
Численный метод также является источником погрешностей. Это связано, например, с заменой интеграла суммой, усечением рядов при вычислениях значений функций, интерполированием табличных данных и т. п. Как правило, погрешность численного метода регулируема, т. е. она может быть уменьшена до любого разумного значения путем изменения некоторого параметра (например, шага интегрирования, числа членов усеченного ряда и т.п.). Погрешность метода обычно стараются довести до величины, в несколько раз меньшей погрешности исходных данных. Дальнейшее снижение погрешности не приведет к повышению точности результатов, а лишь увеличит стоимость расчетов из-за необоснованного увеличения объема вычислении.
При вычислениях с помощью ЭВМ неизбежны погрешности округлений, связанные с ограниченностью разрядной сетки машины. Обычно после выполнения операции производится не округление результата, а простое отбрасывание лишних разрядов с целью экономии машинного времени. Правда, в современных машинах предусмотрена свобода выбора программистом способа округления; соответствующими средствами располагают и некоторые алгоритмические языки.
Максимальная относительная погрешность при округлении есть δmax=0.5α1-k, где α - основание системы счисления, к —количество разрядов мантиссы числа. При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.
В современных машинах с памятью, измеряемой в байтах, принята шестнадцатеричная система счисления, и любое число с плавающей точкой содержит шесть значащих цифр. Следовательно, α =16, к = 6, максимальная погрешность округления αmах= 0.5* 16-5 ≈ 0.5* 10-8.
Несмотря на то, что при решении больших задач выполняются миллиарды операций, это вовсе не означает механического умножения погрешности при одном округлении на число операций, так как при отдельных действиях погрешности могут компенсировать друг друга (например, при сложении чисел разных знаков). Вместе с тем иногда погрешности округлений в сочетании с плохо организованным алгоритмом могут сильно исказить результаты.
|
|
|
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число становится иррациональным.
Например, число 0.1 при переводе в двоичную систему счисления примет вид 0.1=0.00011001100... Может оказаться, что с шагом 0.1 нужно при вычислениях пройти отрезок [0,1] от х=1 до х=0; десять шагов не дадут точного значения х=0.
Абсолютная и относительная погрешности
Если А - точное значение некоторой величины, a a - известное приближение к нему, то абсолютной погрешностью приближения a числа А называют некоторую величину Δ(a) удовлетворяющую условию:
Относительной погрешностью называют некоторую величину δ(А), для которой выполняется условие:
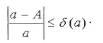
Относительную погрешность часто выражают в процентах.
Информацию о том, что а является приближенным значением числа А с абсолютной погрешностью Δ(а), принято записывать в виде:
Числа а и Δ(а) записываются с одинаковым количеством знаков после запятой.
Информацию о том, что а является приближенным значением числа А с относительной погрешностью δ(а), записывают в виде:
Число δα, заведомо не меньшее относительной погрешности называют предельной относительной погрешностью, т.е.
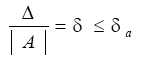
Т.к. на практике A≈ α, то приближенно можно принять, что
Погрешность функции
Пусть искомая величина Y является функцией параметров a1, а2, …, an; т.е. Y = Y(a), и известна область G в пространстве переменных a1, а2, …, an, которой принадлежат параметры. Необходимо получить приближение y к Y и оценить его погрешность.
Если у - приближённое значение величины Y, то предельной абсолютной погрешностью А(у) называют наилучшую при имеющейся информации оценку погрешности величины у:
Предельной относительной погрешностью δ(у) называют величину
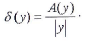
Если задана дифференцируемая функция нескольких независимых переменных 
то предельная абсолютная погрешность этой функции вызываемая погрешностями аргументов 
оценивается величиной
|
|
|
Для оценки предельной относительной погрешности функции имеют место выражения
Пример. Оценить абсолютную и относительную погрешности функции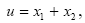 
считая абсолютные предельные погрешности аргументов известными.
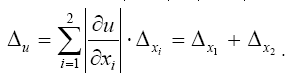
Таким образом, предельная абсолютная погрешность суммы приближенных чисел равна сумме предельных абсолютных погрешностей этих чисел.
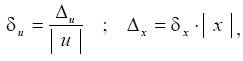тогда если слагаемые одного знака, получаем
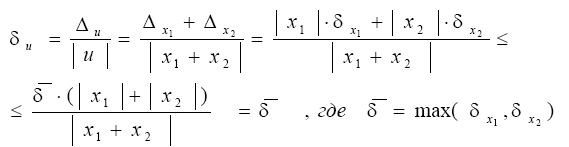
Т.о., если слагаемые одного знака, то предельная относительная погрешность их суммы не превышает наибольшей из предельных относительных погрешностей слагаемых.
Если слагаемые разных знаков, то предельная относительная погрешность суммы вычисляется по формуле
Пример. Оценить абсолютную погрешность функции 
считая абсолютную предельную погрешность аргумента известной.
Таким образом, абсолютная погрешность тангенса всегда больше абсолютной погрешности аргумента.
Пример. Вычислить и определить погрешность результата
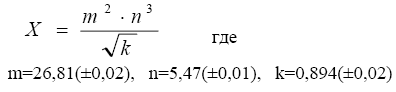
Решение: Произведем вычисления
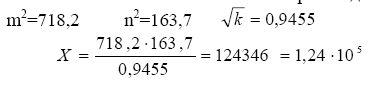
Определим относительные погрешности аргументов
|
|
|
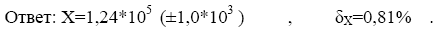
