 |
Занятие № 22. Метод Милна четвертого порядка
|
|
|
|
Цель - ознакомить студентов с методом Милна четвертого порядка решения задачи Коши для обыкновенных дифференциальных уравнений.
Рассмотрим еще один широко известный метод прогноза и коррекции — метод Милна.
Для вывода первой формулы Милна (т.е. формулы предсказания) проинтегрируем данное уравнение (1) на промежутке [ xi-3, xi+1 ] и в полученном интегральном равенстве
(26)
подынтегральную функцию f(x,у(х)) заменим первым интерполяционным многочленом Ньютона Р 3 (х), построенным по четырем узлам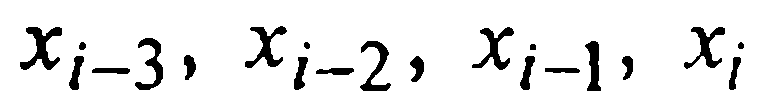 
с предполагающимися уже известными приближенными значениями
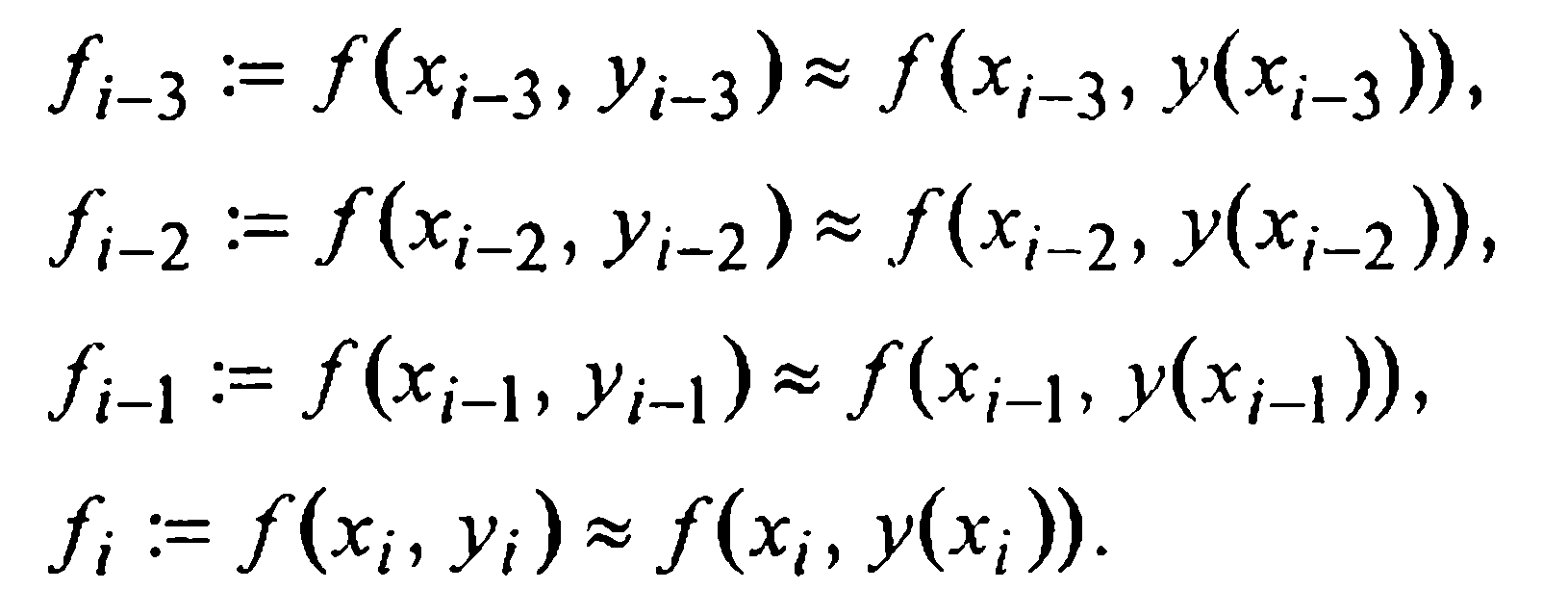
Тогда, после замены переменной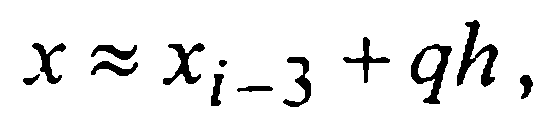 
на основании (26) имеем:
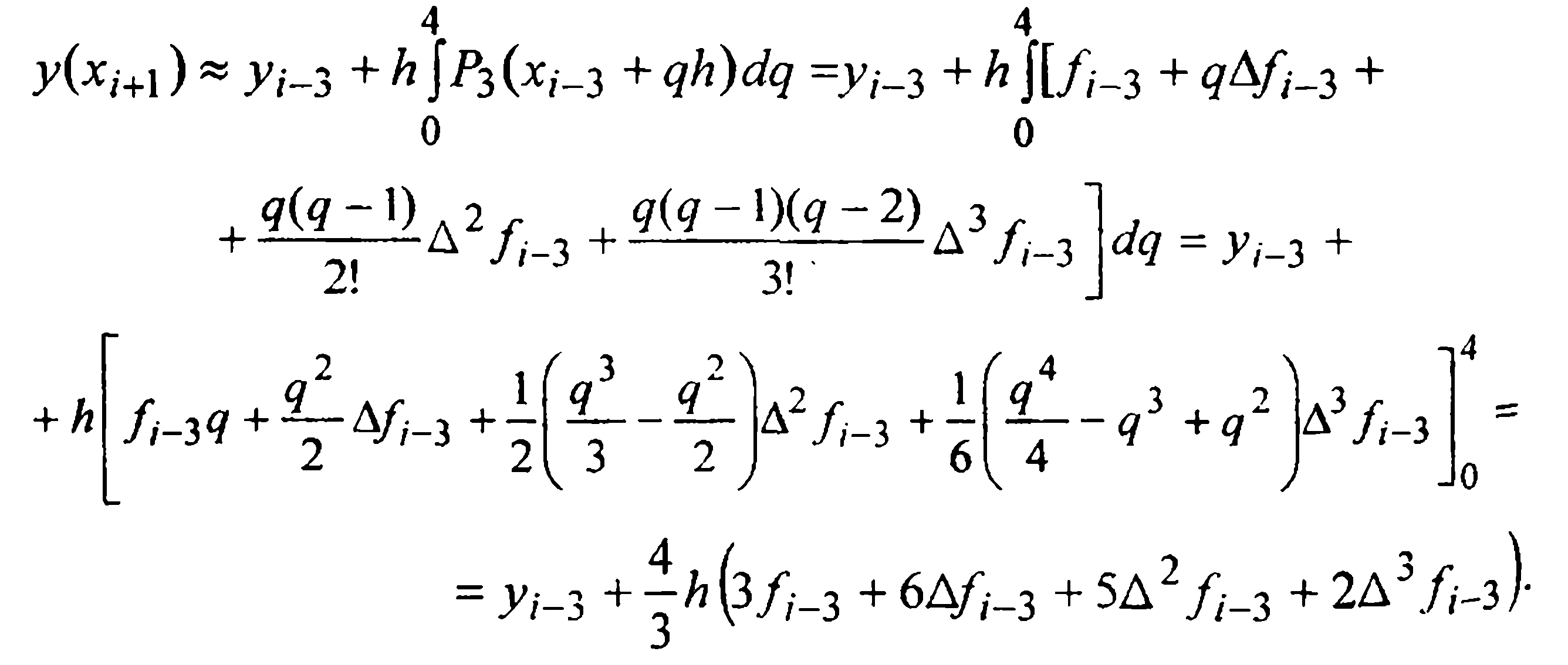
Отсюда, выразив конечные разности через значения функции, получаем первую формулу Милна (предсказания)
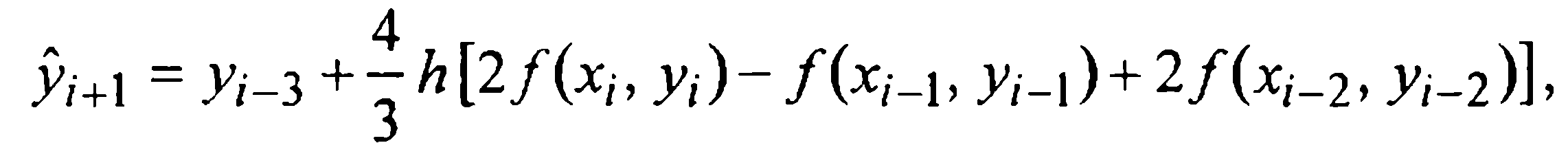(27)
которую, очевидно, следует отнести к экстраполяционным.
Главный член локальной погрешности формулы (27) находим интегрированием следующего (первого из неучтенных) слагаемого интерполяционного многочлена Ньютона. Именно:
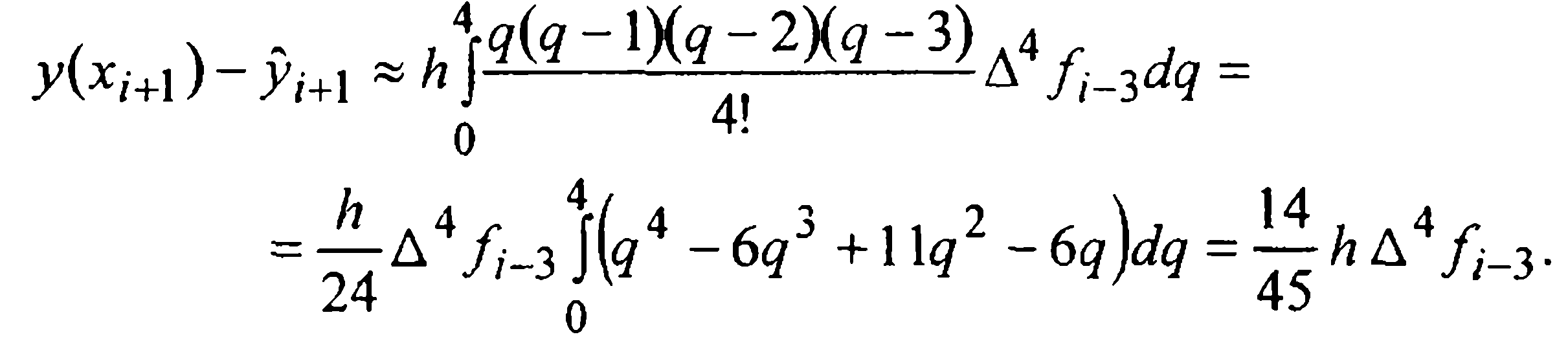
Считая четвертые разности примерно одинаковыми, опустим индекс у функции f в записи 
в результате получаем следующее приближенное представление решения в точке xi+1:
(28)
Вывод второй формулы Милна более прост. Проинтегрируем уравнение (1) теперь на промежутке [ xi-1, xi+1 ] и в полученном равенстве
применим к интегралу простейшую формулу Симпсона. Имеем
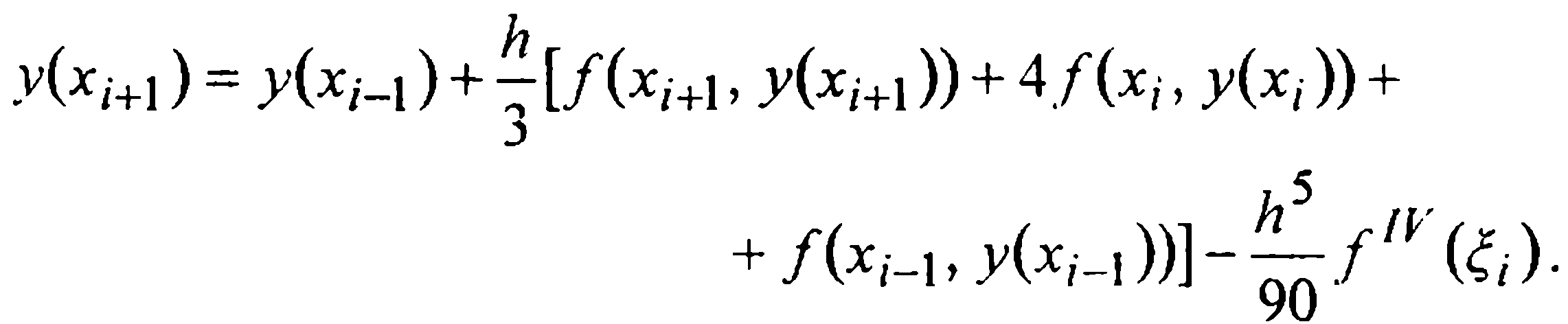(29)
Отбрасывая здесь остаточный член и заменяя значения решения y(xi-1) и y(xi;) известными приближенными значениями yi-1 и yi, а стоящее в правой части под знаком функции f неизвестное значение у(хi+1) тем значением 
которое получается в результате вычислений по явной первой формуле Милна (27), приходим ко второй формуле Милна (уточнения)
|
|
|
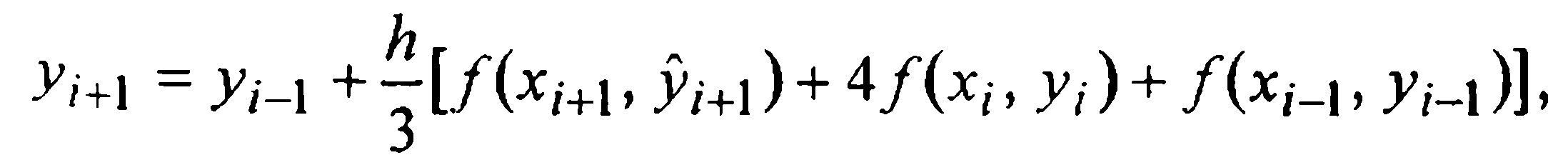(30)
являющейся интерполяционной.
Для вывода приближенной оценки шаговой погрешности воспользуемся приближенным равенством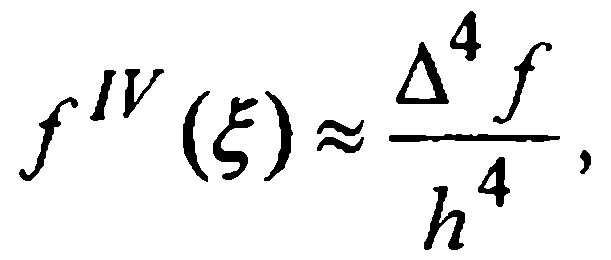 
где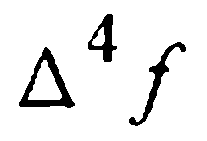 
так же, как и в (28), — условная запись практически постоянных четвертых разностей. Исходя из точного равенства (29), локальную погрешность получаемого с помощью формулы (30) (возможно, с итерационной обработкой, см. замечание) приближенного значения y i+1 можно приближенно охарактеризовать величиной 
, т.е.
(31)
Сравнение (28) и (31) дает:
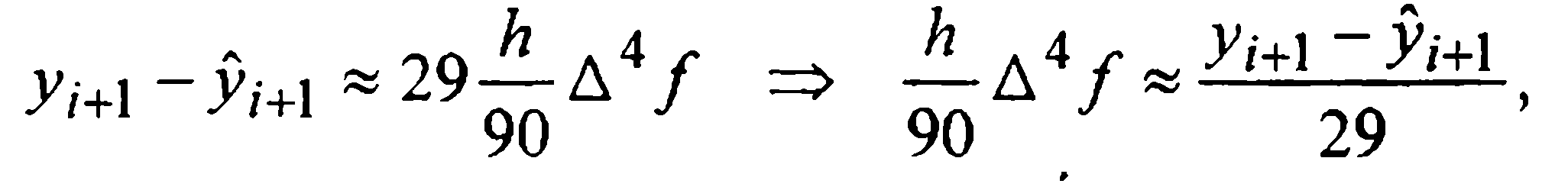
следовательно,
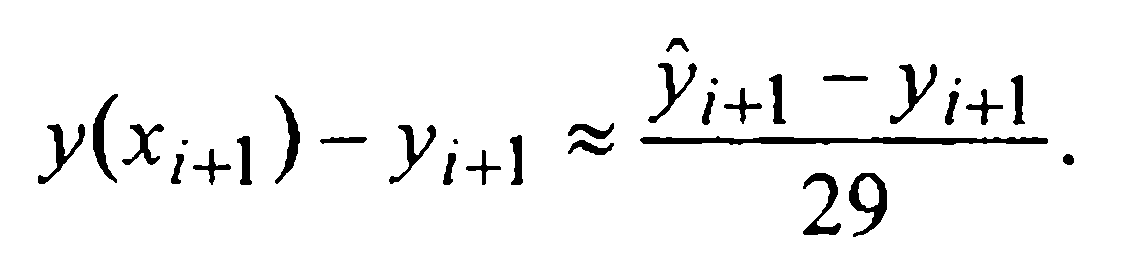(32)
Таким образом, при численном интегрировании начальной задачи (1)-(2) методом Милна четвертого порядка, определенным формулами (27) и (30), на каждом i-м шаге следует вычислять величину
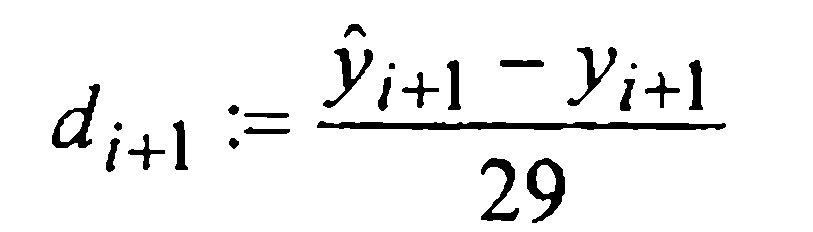
и сравнивать ее модуль с величиной ε > 0 допустимой шаговой погрешности. Если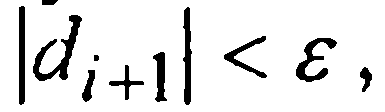 
то за у(хi+1) принимается полученное по второй формуле Милна значение уi+1 (или его уточненное значение 
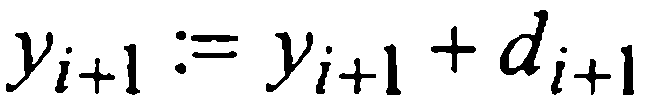); иначе шаг должен быть уменьшен.
Фигурирующая в приближенном равенстве (32) постоянная 1/29 примерно вдвое меньше постоянной 19/270≈1/14 в аналогичном равенстве (24) для предиктор-корректорного метода Адамса четвертого порядка (22), что характеризует метод Милна как несколько более точный при одинаковых вычислительных затратах.
Приложение 1
ПОЛИНОМЫ ЛЕЖАНДРА
Полиномы Лежандра являются специальными функциями, которые применяются при решении многих теоретических и прикладных задач. Полином Лежандра n-й степени можно определить с помощью производной n-го порядка следующим образом:
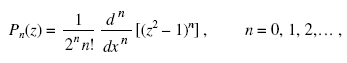(1)
где z - комплексная переменная.
В данном учебном пособии рассматриваются и используются полиномы Лежандра для действительного аргумента x, лежащего в интервале x∈[-1, 1].
С помощью определения (1) легко получить явные выражения полиномов Лежандра действительного аргумента низших степеней:
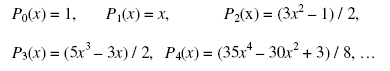(2)
Графики перечисленных полиномов приведены на рис.1.
Все полиномы Лежандра Pn(x) имеют следующие граничные значения:
|
|
|
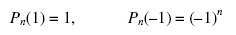(3)
Нетрудно убедиться, что полиномы Лежандра четной степени являются четными функциями и наоборот.
Важным для практических применений является свойство ортогональности полиномов Лежандра:
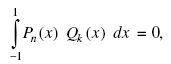(4)
где Qk(x) - любой полином степени k, меньшей n (k < n).
Полиномы Лежандра подчиняются рекуррентному соотношению
(5)
которое, в частности, удобно для последовательного вычисления полиномы высоких степеней.
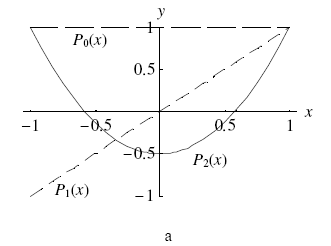
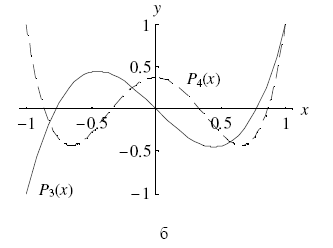
Рис.1. Графики полиномов Лежандра а) n = 0, 1, 2, б) n = 3, 4.
Приложение 2.
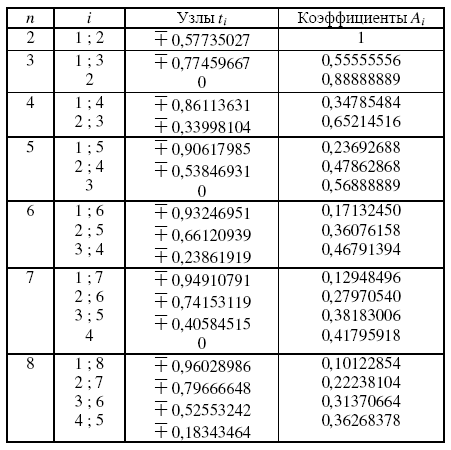
Параметры квадратурных формул Гаусса
|
|
|
