 |
Индивидуальное домашнее задание № 1
|
|
|
|
1. В приведенных задачах числа m, n, k вычислены с некоторой погрешностью. Необходимо вычислить и определить погрешность результата для Х.
1. 
2. 
3. 
4. 

5. 
6. 
7. 
8. 
9. 
10. 
2. Ознакомьтесь с методами приближенного вычисления корней уравнений. Найдите один действительный корень уравнения с точностью 10-5. В ходе решения осуществить следующие шаги:
2.1. Отделить корень уравнения.
2.2. Вычислить с помощью программы значение отдельного корня методами: деление отрезка пополам, хорд, касательных, комбинированным методом, методом итераций. При использовании метода простых итераций найти решение при разных начальных приближениях. Результаты вычислений занести в таблицу.
Вариант задания выбрать из табл. 1.1.

3. Найдите действительный корень уравнения с точностью 10-4, на интервале [a,b]. На первом этапе решения методом деления пополам, уменьшать интервал, содержащий корень, до тех пор, пока его длина не станет меньше 0,2. Потом, применить один из «более» быстрых методов.

| 
| ||

| 
| ||
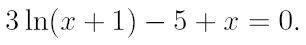
| 
| ||

| 
| ||

| 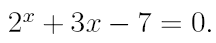
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
ОТЧЕТ О РАБОТЕ
Отчет должен содержать:
1. График исследуемой функции с интервалами отделения корней.
2. Таблицы пошаговых расчетов корня уравнения.
3. Обоснованное заключение о преимуществах и недостатках использования исследованных методов решения применительно к заданному уравнению (для задания 1).
4. Используя схему Гаусса (схема единственного деления и схема полного выбора) решить систему уравнений


5. Решить систему уравнений двумя способами — методом итераций и методом Зейделя. Продолжать итерации до тех пор, пока точность приближенного решения не станет меньше 0,01.
|
|
|


Индивидуальное задание №2.
1. Функция y=f(x) задана таблицей значений:

Указания. Для вариантов 10 - 12 значения аргумента x предварительно перевести из градусов в радианы.
Даны контрольные значения аргумента x1=12; x2=26; x3=42.
a) Написать подходящие для приближенного вычисления значений y1=f(x1), y2=f(x2), y3=f(x3) интерполяционные многочлены Лагранжа первой и второй степени. Получить эти значения.
b) Составить алгоритм и написать программу на языке высокого уровня, реализующую схему Эйткена вычисления с максимально возможной точностью значения y=f(x) в произвольной точке x промежутка  Пользуясь этим алгоритмом, вычислить приближенные значения
Пользуясь этим алгоритмом, вычислить приближенные значения 
c) Сделать анализ результатов заданий 1, 2.
2. Для заданной таблично функции построить все возможные интерполяционные многочлены Ньютона максимальной степени, пригодные для определения значения функции в указанных промежуточных точках  Для всех вариантов
Для всех вариантов 

3. Вычислить значения данной функции и ее прозводной с помощью интерполяционного полинома Лагранжа Ln(x). В качестве узлов интерполяции взять:
1) равномерно распределенные точки на отрезке [a; b];
2) чебышевский набор узлов на отрезке [a; b].
При табулировании функции вычислять ряд с точностью 10-6.
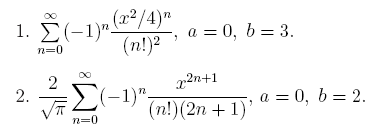


Замечание. При вычислении ряда 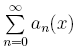 учесть, что каждый последующий член ряда an+1 получается из предыдущего члена an умножением на величину qn, т.е.
учесть, что каждый последующий член ряда an+1 получается из предыдущего члена an умножением на величину qn, т.е.  Это позволит избежать переполнения при вычислении факториалов.
Это позволит избежать переполнения при вычислении факториалов.
4. Найти приближенные значения функции при данных промежуточных значениях аргумента с помощью кубического сплайна и визуализируйте результаты сплайн-интерполяции.


Отчет должен содержать:
ü постановку задачи и исходные данные;
ü описание методов решения;
ü графики, полученных интерполяционных многочленов;
ü листинг программы.
Индивидуальное задание №3
|
|
|
1. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х не является узлом таблицы)
2. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х – узел таблицы)
Таблица 1.
| Вариант | Задание 1. | Задание 2. | |||
| Таблица № | х | Таблица № | х | Используемая формула | |
| 3.0 | 2 (взять 5 последних значений) | 5,3 | Лагранжа | ||
| 3.5 | 3 (взять 4 последних значения) | 6,7 | Лагранжа | ||
| 2.5 | 2,6 | Ньютона | |||
| 5.8 | -3,2 | Ньютона | |||
| 3.1 | 2,3 | Ньютона | |||
| 3.9 | 2,1 | Ньютона | |||
| 3.3 | 4 (взять 5 первых значений) | -0,8 | Лагранжа | ||
| 6.0 | 5 (взять 4 первых значения) | 3,8 | Лагранжа | ||
| 3.2 | 2 (взять 5 первых значений) | 2,9 | Лагранжа | ||
| 5.3 | 1,6 | Ньютона | |||
| 3.9 | 3,4 | Ньютона | |||
| 7.2 | 5 (взять 4 первых значения) | Лагранжа | |||
| 4.4 | 6,2 | Ньютона | |||
| 3.6 | 3 (взять 5 последних значений) | 4,5 | Лагранжа | ||
| 2.2 | 4 (взять 5 последних значений) | Лагранжа | |||
| 6.8 | 3,7 | Ньютона | |||
| 3.4 | 5,6 | Ньютона | |||
| 3.7 | 4 (взять 4 последних значения) | 6,4 | Лагранжа | ||
| 1.8 | 5 (взять 5 первых значений) | 7,4 | Лагранжа | ||
| 7.6 | 4,5 | Ньютона |
Таблица 2.
| Таблица 3.
| ||||||||||||||||||||||||||||||||
Таблица 4.
| Таблица 5.
|
3. Вычислить значения интеграла, используя квадратурные формулы:
· левых прямоугольников,
· правых прямоугольников,
· центральных прямоугольников,
· трапеции,
· Симпсона,
· Ньютона,
· Гаусса с двумя узлами.
Интеграл вычислить с точностью ε=10-6. Точность вычисления интеграла определяется сравнением результатов при различном числе разбиений отрезка интегрирования. Именно, точность ε считается достигнутой, если

здесь  - значение составной квадратурной формулы при разбиении отрезка на N частей.
- значение составной квадратурной формулы при разбиении отрезка на N частей.
Отчет должен содержать:
· постановку задачи и исходные данные,
|
|
|
· описание методов решения и расчетные формулы,
· таблицы значений интегралов с указанием числа разбиений, потребовавшихся для достижения заданной точности,
· листинг программы.
Варианты заданий.
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6. 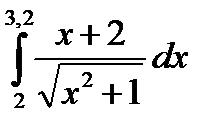 7.
7.  8.
8. 
9.  10.
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15.  16.
16. 
17.  18.
18.  19.
19.  20.
20. 
|
|
|



 -cos(0,4-0,7 x)
-cos(0,4-0,7 x)