 |
Правила вычисления пределов функции.
|
|
|
|
Понятие о пределе числовой последовательности.
Последовательностью называется совокупность значений функции 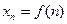 натурального аргумента n.
натурального аргумента n.
Определение 1.1. Число а называется пределом числовой последовательности 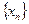 , если для любого
, если для любого  существует такое число N, что
существует такое число N, что  при
при  .
.
В этом случае пишут:  . Определение предела последовательности можно записать с использованием логических кванторов (
. Определение предела последовательности можно записать с использованием логических кванторов ( - квантор общности, читается «для любого» или «для всех»;
- квантор общности, читается «для любого» или «для всех»;  - квантор существования, читается «существует» или «найдется»):
- квантор существования, читается «существует» или «найдется»):
 , если
, если 
Последовательность, имеющая предел, называется сходящейся. Для того, чтобы последовательность имела предел, необходимо и достаточно, чтобы она была монотонной и ограниченной. Предел последовательности единственен, если он существует. Если 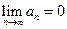 , то последовательность
, то последовательность  называется бесконечно малой.
называется бесконечно малой.
J Пример 1.1. Рассмотрим последовательность 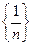 . С ростом n члены последовательности уменьшаются и становятся сколь угодно мало отличающимися от 0. Докажем, что
. С ростом n члены последовательности уменьшаются и становятся сколь угодно мало отличающимися от 0. Докажем, что  .
.
По определению предела  , если
, если  . Положим
. Положим  . Тогда
. Тогда 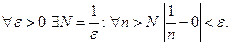 Это означает, что
Это означает, что  . J
. J
Если последовательности  - бесконечно малые, а
- бесконечно малые, а  - ограниченная последовательность, то последовательности
- ограниченная последовательность, то последовательности 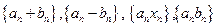 являются бесконечно малыми.
являются бесконечно малыми.
J Пример 1.2.  , т.к.
, т.к. 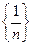 - бесконечно малая, а
- бесконечно малая, а  - ограниченная последовательность. J
- ограниченная последовательность. J
Если 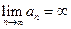 , то последовательность
, то последовательность  называется бесконечно большой. Если последовательность бесконечно большая, то она не ограничена.
называется бесконечно большой. Если последовательность бесконечно большая, то она не ограничена.
J Пример 1.3.  , т.к.члены последовательности
, т.к.члены последовательности  с ростом n растут и становятся сколь угодно большими при больших n. J
с ростом n растут и становятся сколь угодно большими при больших n. J
Правила вычисления пределов последовательностей.
1.  ; 2.
; 2.  ; 3.
; 3.  ;
;
4.  ; 5.
; 5. 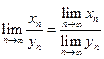 при условии
при условии  .
.
J Пример 1.4. Найти пределы: 1) 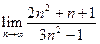 ; 2)
; 2) 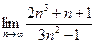 ; 3)
; 3)  .
.
Решение.
1) При  числитель и знаменатель стремятся к бесконечности. Преобразуем данную последовательность, разделив все члены дроби на
числитель и знаменатель стремятся к бесконечности. Преобразуем данную последовательность, разделив все члены дроби на  . Используя правила нахождения пределов, найдём:
. Используя правила нахождения пределов, найдём:  .
.
|
|
|
2) Разделим все члены дроби на  и используем необходимые правила:
и используем необходимые правила:  .
.
3) Разделим все члены дроби на  , получим:
, получим:  . J
. J
Воспользуемся результатами приведённых примеров. Если в условии задачи имеем неопределенность вида  , то:
, то:
1) если старшие степени n в числителе и знаменателе равны, то ответ равен отношению
коэффициентов при данных степенях
2) если старшая степень n находится в числителе, то ответ будет  ;
;
3) если старшая степень находится в знаменателе, то ответ будет 0.
Если  , то последовательности
, то последовательности  и
и  называются эквивалентными, обозначение:
называются эквивалентными, обозначение:  . В решении примеров последовательности можно заменять эквивалентными. Рассмотрим решение примера 1.4 с использованием эквивалентностей:
. В решении примеров последовательности можно заменять эквивалентными. Рассмотрим решение примера 1.4 с использованием эквивалентностей:
1) 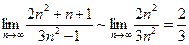 ; 2)
; 2)  ; 3)
; 3)  .
.
J Пример 1.5. Найти  .
.
Решение.
Рассмотрим числитель  . Знаменатель эквивалентен 3n. Таким образом,
. Знаменатель эквивалентен 3n. Таким образом, 
 . J
. J 
J Пример 1.6. Найти 
Решение.
Перейдем к эквивалентным последовательностям и найдем предел их отношения:  . J
. J
J Пример 1.7. Найти 
Решение.
Имеем неопределенность вида  . Избавимся от иррациональности и рассмотрим неопределенность
. Избавимся от иррациональности и рассмотрим неопределенность  .
.
 =
= 
 =
=
 J
J
И от того, что что-то очень сложно, ты не
пытаешься это сделать? Научиться ходить
вначале тоже было тяжело, но ты позани-
мался, и теперь, глядя на тебя, может пока-
заться, что это все не трудно.
Р. Бах. Иллюзии
☼ Упражнения 1.1. Вычислить пределы:
1)  ; 5)
; 5)  ; 9)
; 9)  ;
; 
2)  ; 6)
; 6)  ; 10)
; 10)  ;
;
3)  ; 7)
; 7)  ; 11)
; 11) 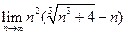 ;
;
4)  ; 8)
; 8)  ; 12)
; 12)  . ☼
. ☼
Число е.
Последовательность 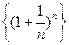 монотонная и ограниченная. Следовательно, она имеет конечный предел. Этот предел определяет эйлерово число
монотонная и ограниченная. Следовательно, она имеет конечный предел. Этот предел определяет эйлерово число  . Число е – иррациональное, е
. Число е – иррациональное, е  .
.
J Пример 1.7. Найти пределы: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение.
1)  .
.
2) 
 .
.
3)  . J
. J
- Надо же как все просто.
- Как научиться ходить. Потом ты начинаешь
удивляться, что в этом было такого сложного.
|
|
|
Р. Бах. Иллюзии
☼ Упражнения 1.2. Вычислить пределы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 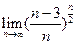 ;
;
6) 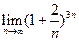 ; 7)
; 7)  ; 8)
; 8)  . ☼
. ☼
Предел функции.
Пусть функция f(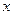 ) определена на некотором промежутке Х и пусть точка
) определена на некотором промежутке Х и пусть точка  или
или  .
.
Определение 1.2. Число А называется пределом функции  (
(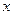 ) в точке
) в точке  , если
, если  такое, что для всех
такое, что для всех  ,
,  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 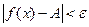 .
.
Записывается так: 
J Пример 1.8. Используя определение, докажем, что функция 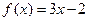 в точке
в точке  имеет предел, равный единице, т.е.
имеет предел, равный единице, т.е. 
Возьмем любое  . Найдем такое
. Найдем такое  , при котором из неравенства
, при котором из неравенства  следовало бы неравенство
следовало бы неравенство  . Преобразуя неравенство, получаем
. Преобразуя неравенство, получаем  . Отсюда видно, что если взять
. Отсюда видно, что если взять 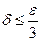 , то для всех
, то для всех 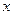 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется требуемое неравенство
, выполняется требуемое неравенство  . Это и означает, что
. Это и означает, что  В частности, если
В частности, если  , то
, то  . J
. J
☼ Упражнения 1.3. Используя определение, доказать, что:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 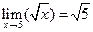 ;
;
5) 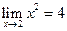 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  . ☼
. ☼
Правила вычисления пределов функции.
Пусть функции  и
и  имеют в точке
имеют в точке  пределы В и A. Тогда
пределы В и A. Тогда
1. 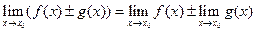 =
= 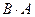 ;
;
2.  ; 3.
; 3.  (при
(при  ).
).
4.  ; 5.
; 5.  = С
= С  B;
B;
Правила верны также и в случае, когда  является одним из символов
является одним из символов  или
или  .
.
J Пример 1.9. Найти  .
.
Решение.
По правилам вычисления предела функции находим
 =
=  . J
. J
☼ Упражнения 1.4. Найти пределы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  . ☼
. ☼
1.6. Раскрытие неопределенностей вида  и
и  .
.
J Пример 1.10. Найти  .
.
Решение.
Имеем неопределенность вида 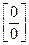 . Разложим числитель и знаменатель на множители и сократим на общий множитель, который обращает в нуль числитель и знаменатель дроби:
. Разложим числитель и знаменатель на множители и сократим на общий множитель, который обращает в нуль числитель и знаменатель дроби: 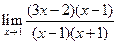 =
=  . J
. J
J Пример 1.11. Найти  .
.
Решение.
Имеем неопределенность вида  . Так же, как и в случае последовательностей заменим бесконечно большие функции на эквивалентные и найдем предел дроби:
. Так же, как и в случае последовательностей заменим бесконечно большие функции на эквивалентные и найдем предел дроби: 
 . J
. J
J Пример 1.12. Найти  .
.
Решение.
Имеем неопределенность вида  . Заменим бесконечно большие функции на эквивалентные и найдем предел дроби:
. Заменим бесконечно большие функции на эквивалентные и найдем предел дроби:  . J
. J
J Пример 1.13. Найти  .
.
Решение.
Имеем неопределенность вида  . Заменим бесконечно большие функции на эквивалентные и найдем предел дроби:
. Заменим бесконечно большие функции на эквивалентные и найдем предел дроби:  . J
. J
Сопоставляя результаты решений примеров 1.11 - 1.13 установим правило нахождения пределов с неопределенностью  . Если
. Если  - многочлены степеней m и k соответственно, то
- многочлены степеней m и k соответственно, то 
где  - отношение коэффициентов при старших степенях многочленов.
- отношение коэффициентов при старших степенях многочленов.
J Пример 1.14. Вычислить  .
.
Решение.
Учитывая условие  , получаем
, получаем 
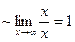 .J
.J
|
|
|
☼ Упражнения 1.5. Найти пределы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5) 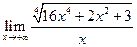 ; 6)
; 6)  ; 7)
; 7)  ;
;
8)  ; ☼
; ☼
1.7. Раскрытие неопределенности вида  .
.
Неопределенность вида  при помощи алгебраических преобразованийприводится к неопределенности
при помощи алгебраических преобразованийприводится к неопределенности  .
.
J Пример 1.15. Найти  .
.
Решение.
Имеем неопределенность вида  . Умножим и разделим рассматриваемое выражение на сопряженное и заменим знаменатель на эквивалентную величину:
. Умножим и разделим рассматриваемое выражение на сопряженное и заменим знаменатель на эквивалентную величину:  =
=  . J
. J
J Пример 1.16. Найти  .
.
Решение.
Имеем неопределенность вида  . Для вычисления этого предела используем прием умножения и деления на сопряженное выражение:
. Для вычисления этого предела используем прием умножения и деления на сопряженное выражение:
 =
= 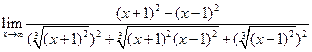 =
=
=  =
=  . J
. J
J Пример 1.17. Найти  .
.
Решение.
Имеем неопределенность вида  . Преобразуем данное выражение и
. Преобразуем данное выражение и
найдем предел дроби:
 =
=  =
=  =
=  =
=  . J
. J
☼ Упражнения 1.6. Найти пределы:
1)  ; 2)
; 2)  ; 3)
; 3) 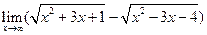 ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  . ☼
. ☼
|
|
|


