 |
Два замечательных предела.
|
|
|
|
Рассмотрим два предела, имеющих важное значение.
Первый замечательный предел:  .
.
J Пример 1.18. Найти 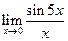 .
.
Решение.
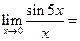
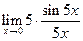
 . J
. J
J Пример 1.19. Найти  .
.
Решение.
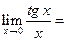
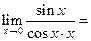
 . J
. J
J Пример 1.20. Найти 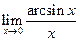 .
.
Решение.
Положим  . Тогда
. Тогда 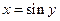 . Заметим, что
. Заметим, что  при
при 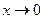 . Имеем:
. Имеем:

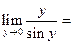
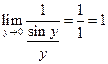 . J
. J
Аналогичным образом, принимая во внимание, что 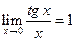 , можно установить, что
, можно установить, что
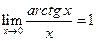 .
.
J Пример 1.21. Найти 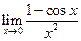 .
.
Решение.



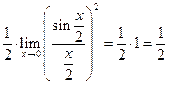 . J
. J
Второй замечательный предел: 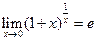 .
.
J Пример 1.22. Найти 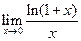 .
.
Решение.
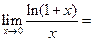
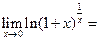
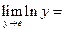
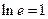 . J
. J
J Пример 1.23. Найти 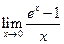 .
.
Решение.
Положим  . Тогда
. Тогда 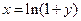 . Заметим, что
. Заметим, что  при
при 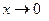 .
.

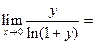
 . J
. J
Полученное соотношение является частным случаем предела
 , для получения которого использовались преобразования:
, для получения которого использовались преобразования:
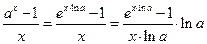
 .
.
Сравнение бесконечно малых.
Функция 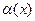 называется бесконечно малой при
называется бесконечно малой при 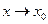 , если
, если 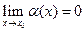 . Пусть
. Пусть 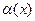 и
и 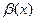 - две бесконечно малые функции при
- две бесконечно малые функции при 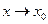 . Тогда:
. Тогда:
1) если 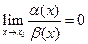 , то
, то 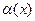 называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем 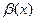 ;
;
2) если  , то
, то 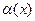 и
и 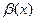 называются бесконечно малыми одного порядка;
называются бесконечно малыми одного порядка;
3)если 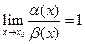 , то
, то 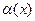 и
и 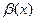 называются эквивалентными бесконечно малыми. Обозначение:
называются эквивалентными бесконечно малыми. Обозначение: 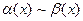 ;
;
4)если 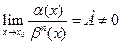 , то
, то 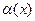 называется бесконечно малой n-го порядка относительно
называется бесконечно малой n-го порядка относительно 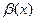 ;
;
J Пример 1.24. Доказать, что при 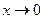 функции
функции 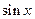 и
и 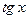 - эквивалентные бесконечно малые (
- эквивалентные бесконечно малые ( при
при 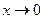 ).
).
Решение. Действительно,  . J
. J
Результаты решения примеров 1.19 - 1.23 являются следствиями из 1-го и 2-го замечательных пределов. Запишем эти следствия и некоторые другие, получающиеся подобным образом,
в виде таблицы эквивалентных бесконечно малых. При 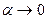
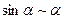
| 
| 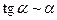
| 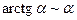
| 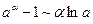
| 
|
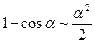
| 
| 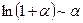
| 
| 
|
J Пример 1.25. Найти 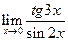 .
.
Решение.
При 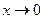
 и
и  и, значит,
и, значит, 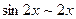 ,
,  . Заменяя числитель и знаменатель на эквивалентные бесконечно малые, получаем
. Заменяя числитель и знаменатель на эквивалентные бесконечно малые, получаем  . J
. J
J Пример 1.26. Найти 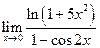 .
.
Решение.
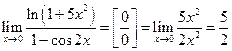 . J
. J
J Пример 1.27. Найти  .
.
Решение.
 =
= 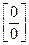 =
= 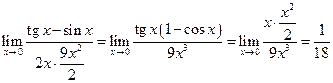 . J
. J
J Пример 1.28. Найти 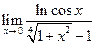 .
.
Решение.
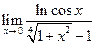

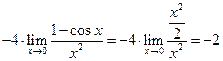 . J
. J
|
|
|
- Мой дорогой Уотсон, попробуйте немного
проанализировать сами, - сказал он с легким
раздражением.- Вы знаете мой метод. При-
мените его, и будет поучительно сравнить
результаты.
А.Л. Дойл. Знак четырех.
☼ Упражнения 1.7. Найти пределы:
1) 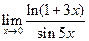 ; 2)
; 2) 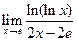 ; 3)
; 3)  ; 4)
; 4) 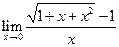 ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 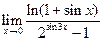 ; ☼
; ☼
II. Дифференцирование.
Понятие производной.
По определению производной функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента при условии
называется предел отношения приращения функции к приращению аргумента при условии 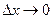 . Производная обозначается
. Производная обозначается  или
или 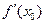 . Тогда
. Тогда 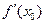
 .
.
Нахождение производной называется дифференцированием функции.
J Пример 2.1. Найти производную функции 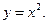
Решение.
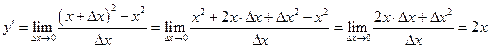 . J
. J
☼ Упражнения 2.1. Используя определение производной, найти производные функций в точке  : 1)
: 1)  ; 2)
; 2)  ; 3)
; 3) 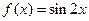 . ☼
. ☼
Вычисление производных.
Правила дифференцирования.
Если функции 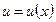 и
и 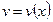 имеют производные в точке
имеют производные в точке  , то в этой точке имеют производные их сумма, разность, произведение и частное, причём:
, то в этой точке имеют производные их сумма, разность, произведение и частное, причём:
1) 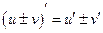 ;
;
2) 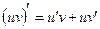 ;
;
3) 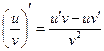 при
при 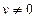 ;
;
4) если функция 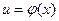 дифференцируема в точке
дифференцируема в точке  ,
,
а функция  дифференцируема в точке
дифференцируема в точке 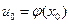 ,
,
то сложная функция  дифференцируема в точке
дифференцируема в точке  и
и
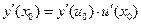 .
.
Таблица производных.
| № | 
| 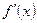
| № | 
| 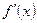
|
| 1. | 
| 10. | 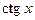
| 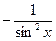
| |
| 2. | 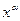
| 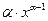
| 11. | 
| 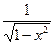
|
| 3. | 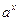
| 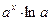
| 12. | 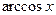
| 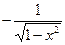
|
| 4. | 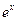
| 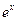
| 13. | 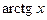
| 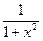
|
| 5. | 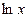
| 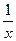
| 14. | 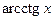
| 
|
| 6. | 
| 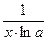
| 15. | 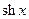
| 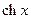
|
| 7. | 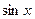
| 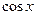
| 16. | 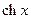
| 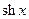
|
| 8. | 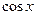
| 
| 17. | 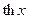
| 
|
| 9. | 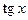
| 
| 18. | 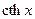
| 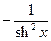
|
J Пример 2.2. Найти производные функций: 1)  ; 2)
; 2) 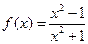 ; 3)
; 3) 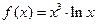 ; 4)
; 4) 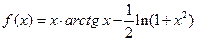 ; 5)
; 5) 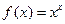 ;
;
6) 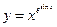 ; 7)
; 7) 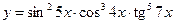 ; 8)
; 8) 
 .
.
Решение.
1) 
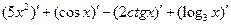 =
= 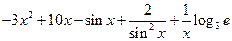 ;
;
2) 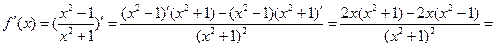
 ;
;
3) 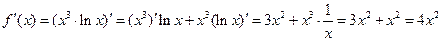 ;
;
4) 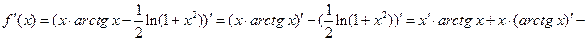
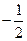
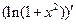 =
= 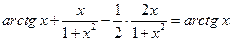 ;
;
5) Чтобы найти производную функции 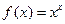 , прологарифмируем уравнение:
, прологарифмируем уравнение: 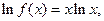
 и тогда
и тогда 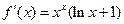 ;
;
6) Для того, чтобы найти производную степенно-показательной функции, прологарифмируем уравнение: 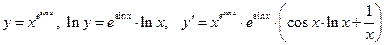 ;
;
7) Чтобы найти производную функции 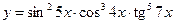 также прологарифмируем уравнение, получим сумму логарифмов и дифференцирование станет проще:
также прологарифмируем уравнение, получим сумму логарифмов и дифференцирование станет проще: 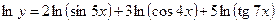 ,
, 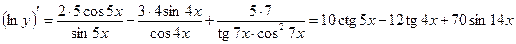 , тогда
, тогда
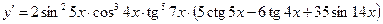 ;
;
8) Используем логарифмическое дифференцирование для нахождения производной функции 
 :
:  ,
,
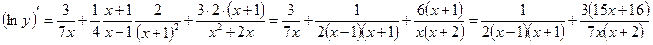 ,
,
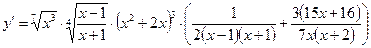 . J
. J
Я занимался до сих пор решением ряда
задач, ибо при изучении наук примеры
полезнее правил.
|
|
|
И. Ньютон. Всеобщая арифметика
☼ Упражнения 2.2. Найти производные функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 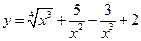 ; 5)
; 5) 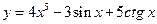 ; 6)
; 6)  ;
;
7) 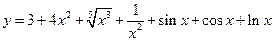 ; 8)
; 8) 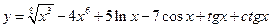 ;
;
9)  ; 10)
; 10)  ; 11)
; 11)  ;
;
12) 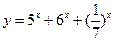 ; 13)
; 13) 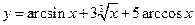 ; 14)
; 14) 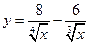 ;
;
15) 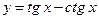 ; 16)
; 16) 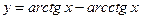 ; 17)
; 17)  ; 18)
; 18) 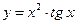 ;
;
19) 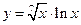 ; 20)
; 20) 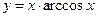 ; 21)
; 21)  ; 22)
; 22) 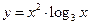 ;
;
23)  ; 24)
; 24) 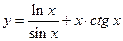 ; 25)
; 25) 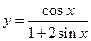 ; 26)
; 26)  ;
;
27) 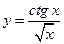 ; 28)
; 28) 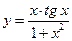 ; 29)
; 29) 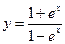 ; 30)
; 30) 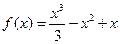 , найти
, найти
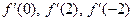 ; 31)
; 31)  ; 32)
; 32) 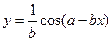 ; 33)
; 33) 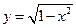 ;
;
34) 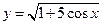 ; 35)
; 35)  ; 36)
; 36)  ; 37)
; 37)  ;
;
38) 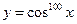 ; 39)
; 39) 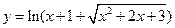 ; 40)
; 40) 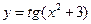 ; 41)
; 41) 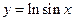 ;
;
42) 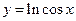 ; 43)
; 43)  ; 44)
; 44)  ; 45)
; 45)  46)
46) 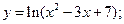
47) 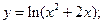 48)
48) 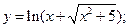 49)
49) 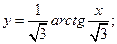 50)
50)  ;
;
51) 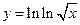 ; 52)
; 52) 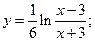 53)
53) 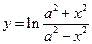 ; 54)
; 54) 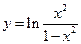 ; 55)
; 55) 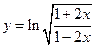 ;
;
56) 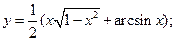 57)
57) 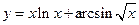 ; 58)
; 58) 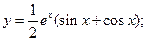
59) 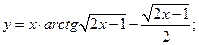 60)
60) 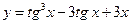 ; 61)
; 61) 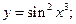 62)
62) 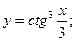
63) 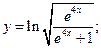 64)
64) 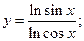 65)
65) 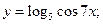 66)
66) 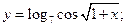
67) 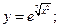 68)
68)  69)
69)  70)
70) 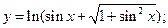
71) 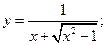 72)
72)  73)
73) 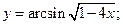 74)
74) 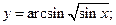
75)  76)
76) 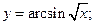 77)
77) 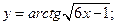 78)
78) 
79)  80)
80) 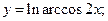 81)
81)  82)
82) 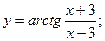
83) 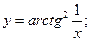 84)
84) 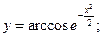 85)
85) 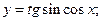 86)
86) 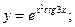
87)  88)
88) 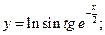 89)
89)  90)
90) 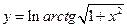 ;
;
91) 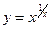 ; 92)
; 92) 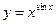 ; 93)
; 93) 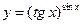 . ☼
. ☼
Дифференциал функции.
Если функция  дифференцируема в точке
дифференцируема в точке 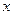 , т.е. имеет в этой точке конечную производную
, т.е. имеет в этой точке конечную производную 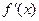 , то ее приращение
, то ее приращение 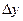 можно записать в виде
можно записать в виде  , где
, где 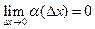 . Главная, линейная относительно
. Главная, линейная относительно 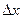 часть
часть 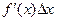 приращения функции
приращения функции
называется дифференциалом функции и обозначается 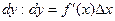 . При достаточно малых
. При достаточно малых 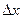 приращение функции приближенно равно ее дифференциалу
приращение функции приближенно равно ее дифференциалу 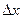 и тогда имеем формулу приближенного значения функции в точке
и тогда имеем формулу приближенного значения функции в точке 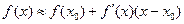 .
.
J Пример 2.3. Найти дифференциал функции 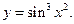
Решение.
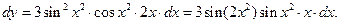 J
J
J Пример 2.4. Вывести формулу 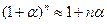 и найти приближенно значение
и найти приближенно значение 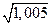 .
.
Решение.
Возьмем функцию 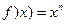 . Тогда при малых
. Тогда при малых 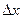
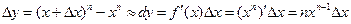 . Следовательно,
. Следовательно, 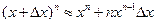 . Полагая
. Полагая 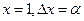 , получим
, получим 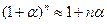 . Найдем приближенно
. Найдем приближенно 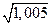 :
: 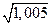
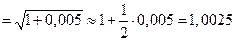 . J
. J
☼ Упражнения 2.3. Найти дифференциалы функций:
1)  ; 2)
; 2) 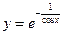 ; 3)
; 3) 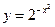 ; 4)
; 4)  ; 5)
; 5) 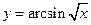 ;
;
6) 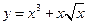 ; 7)
; 7)  ; 8)
; 8) 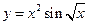 ; 9)
; 9) 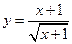 ; 10)
; 10) 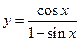 ;
;
11)  ; 12)
; 12)  ; 13)
; 13)  ;
;
14) Вывести приближенную формулу 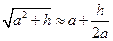 и найти приближенно
и найти приближенно  ; 15) Найти приближенно
; 15) Найти приближенно 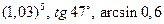 . ☼
. ☼
|
|
|


