 |
Схема построения графика функции.
|
|
|
|
Чтобы не попасть в капкан,
чтобы в темноте не заблудиться,
чтобы никогда в пути не сбиться,
чтобы в нужном месте приземлиться,
приводниться,-
начерти на карте план.
Если даже есть талант-
чтобы не нарушить, не расстроить
чтобы не разрушить, а построить,
чтобы увеличиться, удвоиться, утроиться
нужен очень точный план.
В. Высоцкий. Песня Алисы о планах.
1. Найти область D значений x, где функция  определена.
определена.
2. Найти точки  ,
,  ,
,  , где
, где  или производная не существует,
или производная не существует,
в частности равна  . Вычислить значения
. Вычислить значения  в этих точках:
в этих точках:  ,
,  ,
,  , если они существуют, и определить, не являются ли они точками максимума или минимума. Если
, если они существуют, и определить, не являются ли они точками максимума или минимума. Если  не определена в какой-либо из точек
не определена в какой-либо из точек  , то важно знать пределы
, то важно знать пределы  ,
,  , а также
, а также  ,
,  , если они имеют смысл.
, если они имеют смысл.
3. Область D разделяется точками  на интервалы
на интервалы  , на каждом из которых
, на каждом из которых  . Среди них могут быть бесконечные интервалы вида
. Среди них могут быть бесконечные интервалы вида  или
или  . Будем считать, что производная
. Будем считать, что производная 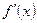 непрерывна на каждом таком интервале
непрерывна на каждом таком интервале  . Тогда
. Тогда 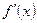 на
на  сохраняет знак. Выясним, какой это знак. Тогда будет известно, возрастает или убывает функция
сохраняет знак. Выясним, какой это знак. Тогда будет известно, возрастает или убывает функция  на
на  .
.
4. Важно отметить на каждом интервале  точки
точки  ,
,  ,
,  , где
, где  , и определить соответствующие значения функции
, и определить соответствующие значения функции  ,
,  ,
,  . В этих точках могут быть точки перегиба кривой
. В этих точках могут быть точки перегиба кривой  . Эти точки делят
. Эти точки делят  на интервалы, на которых вторая производная
на интервалы, на которых вторая производная  , если она существует, сохраняет знак. Выяснение знака
, если она существует, сохраняет знак. Выяснение знака  даёт возможность узнать направление выпуклости кривой.
даёт возможность узнать направление выпуклости кривой.
5. По возможности решить уравнение  и выяснить интервалы, на которых
и выяснить интервалы, на которых  сохраняет знак (
сохраняет знак ( ,
,  ).
).
6. Выяснить вопрос о существовании асимптот, то есть найти пределы  ,
,  .
.
7. На основе сведений построить график функции  .
.
J Пример 3.1. Исследовать функцию  и построить её график.
и построить её график.
1.  .
.
2. Функция общего вида.
3.  ,
,  , поэтому вертикальных асимптот нет.
, поэтому вертикальных асимптот нет.
|
|
|
4. Так как функция не определена при  и
и  , понятие горизонтальной или наклонной асимптоты для неё не имеет смысла.
, понятие горизонтальной или наклонной асимптоты для неё не имеет смысла.
5. Экстремумы и интервалы монотонности:
 , ,
 при при  , ,
 . .
| 
|
6. Точки перегиба и интервалы выпуклости:
 ,
,
 , поэтому
, поэтому  и функция выпукла вверх на отрезке
и функция выпукла вверх на отрезке  . Точек перегиба нет.
. Точек перегиба нет.
График функции представлен на рис. 4. J

| 
|
| Рис. 4. | Рис. 5. |
J Пример 3.2. Исследовать функцию  и построить её график.
и построить её график.
1.  .
.
2. Функция общего вида.
3. Вертикальных асимптот нет.
4.  , поэтому горизонтальных асимптот нет.
, поэтому горизонтальных асимптот нет.
Есть ли наклонные асимптоты?  ,
,

 – наклонная асимптота.
– наклонная асимптота.
5. Экстремумы и интервалы монотонности:
 , ,
 при при  , ,  не существует при не существует при  , ,  при при  . .
| 
|
 – точка локального максимума,
– точка локального максимума,  ;
;  – точка локального минимума,
– точка локального минимума,  .
.
6. Точки перегиба и интервалы выпуклости:
 ,
,
 при при  , ,  не существует при не существует при  . .
 – точка перегиба. – точка перегиба.
| 
|
7.  при
при  и
и  .
.
График функции представлен на рис. 5. J
- Задай еще вопрос. Какое же наслаждение
наблюдать за работой собственной головы,
решающей мировые проблемы!
Р. Бах. Иллюзии
☼ Упражнения 3.1. Построить графики функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10) 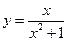
11)  ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15) 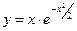 ; 16)
; 16)  ; 17)
; 17)  ; 18)
; 18)  ; 19)
; 19)  ; 20)
; 20)  ; 21)
; 21)  ;
;
22)  ; 23)
; 23)  ; 24)
; 24)  ; 25)
; 25)  ;
;
26)  ; 27)
; 27)  . ☼
. ☼
Я просил его присутствовать, ибо сегодня он
услышит ответы на свои вопросы.
Дж.Р.Р. Толкин. «Властелин Колец».
Ответы, указания.
Глава 1.
1.1. 1)  ; 7)
; 7) 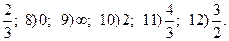
1.2. 1) 
1.4. 1) 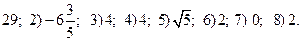
1.5. 1) 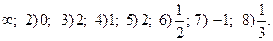
1.6. 1) 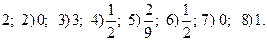
1.7. 1) 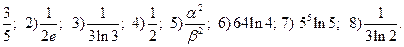
Глава 2.
2.1. 1) 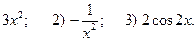
2.2. 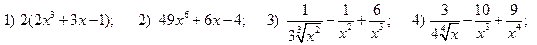
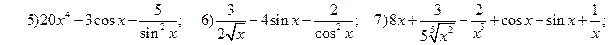
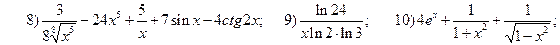
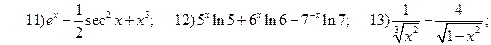
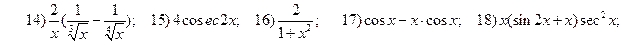
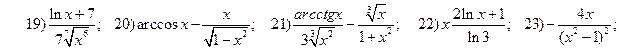
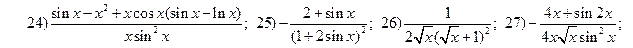
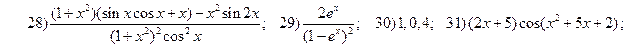
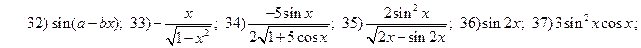
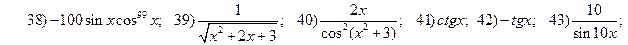
 ;
;
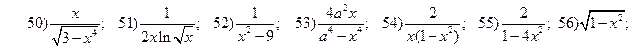
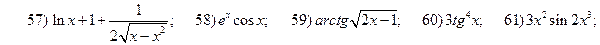
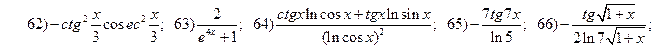
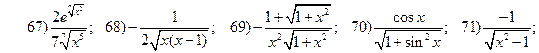
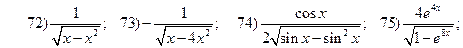
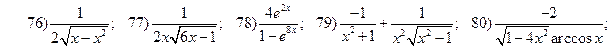
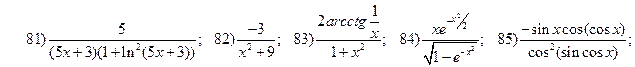
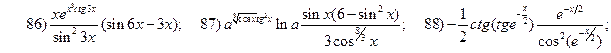

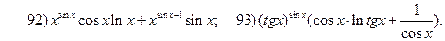
2.3. 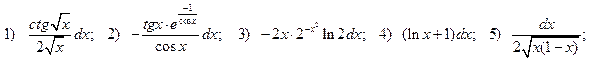
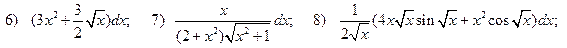
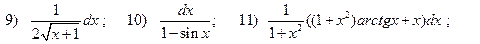
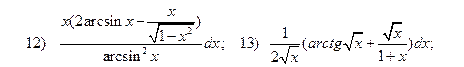
14) 10,05; 1,02; 6,41; 2,08; 2,01; 15) 1,15; 1,072;  .
.
2.4. 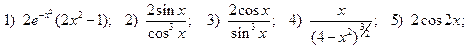
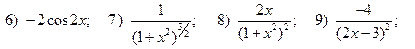
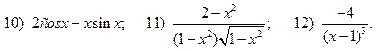
2.5. 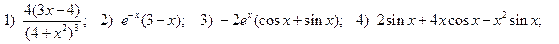
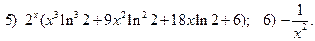
2.6. 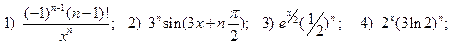
5)  ;
; 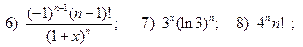
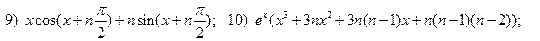
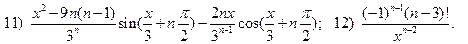
2.7. 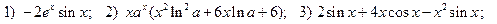

2.8. 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
.
Глава 3.
3.1. 1) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ; при
; при  - точка перегиба;
- точка перегиба;
2) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ; при
; при  - точка перегиба;
- точка перегиба;
3) Область определения функции  . При
. При  - максимум,
- максимум,  , при
, при  выпуклость вверх;
выпуклость вверх;
4) При  - максимум,
- максимум,  ; при
; при  - точка перегиба;
- точка перегиба;  - горизонтальная асимптота при
- горизонтальная асимптота при  ;
;
5) Область определения 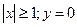 - горизонтальная асимптота;
- горизонтальная асимптота;
|
|
|
6) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ;
;
7) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ; при
; при  - точка перегиба,
- точка перегиба,  - горизонтальная асимптота;
- горизонтальная асимптота;
8) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ; при
; при  - точка перегиба;
- точка перегиба;
9) Экстремальных точек нет;  - вертикальные асимптоты,
- вертикальные асимптоты,  - горизонтальная асимптота;
- горизонтальная асимптота;
10) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ; при
; при  ,
,  - точки перегиба;
- точки перегиба;  - горизонтальная асимптота;
- горизонтальная асимптота;
11) При  - максимум,
- максимум,  ; при
; при  - точка перегиба;
- точка перегиба;  - вертикальная асимптота,
- вертикальная асимптота,  - горизонтальная асимптота;
- горизонтальная асимптота;
12) При  - максимум,
- максимум,  ;
;  - вертикальные асимптоты;
- вертикальные асимптоты;  - горизонтальная асимптота;
- горизонтальная асимптота;
13) При  - максимум,
- максимум,  ; при
; при  - точка перегиба;
- точка перегиба;  - горизонтальная асимптота при
- горизонтальная асимптота при  ;
;
14) При  - минимум,
- минимум,  ; точек перегиба нет;
; точек перегиба нет;  - вертикальная асимптота при
- вертикальная асимптота при  ;
;
15) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум, 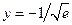 ; при
; при  - точки перегиба;
- точки перегиба;  - горизонтальная асимптота;
- горизонтальная асимптота;
16) При  - максимум,
- максимум,  ; при
; при  - точки перегиба;
- точки перегиба;  - горизонтальная асимптота при
- горизонтальная асимптота при  ;
;
17) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ;
;  - вертикальные асимптоты;
- вертикальные асимптоты;  - горизонтальная асимптота при
- горизонтальная асимптота при  ;
;
18) Экстремальных точек нет. При  - точки перегиба;
- точки перегиба;  - горизонтальные асимптоты;
- горизонтальные асимптоты;  ;
;
19) При  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ;
;  - горизонтальная асимптота; функция неотрицательная.
- горизонтальная асимптота; функция неотрицательная.
20) При  - минимум,
- минимум,  ; функция положительная;
; функция положительная;  - вертикальная асимптота при
- вертикальная асимптота при  ;
;
21) При  - минимум,
- минимум,  ; при
; при  - максимум,
- максимум,  ;
;  - наклонная асимптота;
- наклонная асимптота;  - вертикальная асимптота;
- вертикальная асимптота;
22) При  - максимум,
- максимум,  ; при
; при  - максимум,
- максимум,  ; при
; при  - минимум,
- минимум,  ;
;  - наклонная асимптота;
- наклонная асимптота;  - вертикальная асимптота; при
- вертикальная асимптота; при  - точка перегиба;
- точка перегиба;
23) При  - минимум,
- минимум,  ; точек перегиба нет;
; точек перегиба нет;  - наклонная асимптота;
- наклонная асимптота;  - вертикальная асимптота;
- вертикальная асимптота;
24) При 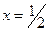 - минимум,
- минимум,  ;
;  - наклонная асимптота при
- наклонная асимптота при  ;
;  - вертикальная асимптота при
- вертикальная асимптота при  ;
;
25) При  - минимум,
- минимум,  ; при
; при  - максимум,
- максимум, 
 - вертикальная асимптота,
- вертикальная асимптота,  - наклонная асимптота;
- наклонная асимптота;
26) При  - минимум, y =
- минимум, y =  ; (1;0) - точка пересечения с осью Ох;
; (1;0) - точка пересечения с осью Ох;  , точек перегиба нет;
, точек перегиба нет;
27) Экстремальных точек нет. При х = 0 – точка перегиба;  - наклонная асимптота при
- наклонная асимптота при  ,
,  - наклонная асимптота при
- наклонная асимптота при  .
.
Литература
- Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: ООО «Издательство АСТ», 2002.
- Кузнецов Л.А. Сборник задач по высшей математике. Типовые расчёты. СПб.: Издательство «Лань», 2005.
- Вельмисова С.Л., Червон С.В. Математический анализ, часть 1. Ульяновск: УлГУ, 2009.
|
|
|


