Главная | Обратная связь | Поможем написать вашу работу!

Предположения линейной регрессии

Стр 1 из 3Следующая ⇒

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ МЕЖДУНАРОДНЫХ ОТНОШЕНИЙ

Кафедра международных экономических отношений

КОНТРОЛЬНАЯ РАБОТА ПО ПРЕДМЕТУ

«ЭКОНОМЕТРИКА И ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ»

Барадулиной Нины Владимировны

студентки 3 курса, специальность

«Мировая экономика»

Научный руководитель:

Коваленко Ирина Васильевна

Минск, 2015

Содержание

Задание 13

Задание 25

Задание 310

Список использованных источников14

Задание 1

Простая (парная) линейная регрессия (ПЛР). Классические предположения моделей

Что такое регрессия?

Регрессия в теории вероятностей и математической статистике —- это математическое выражение, выражающее зависимость зависимой переменной у от независимых переменных х при условии, что это математическое выражение будет иметь статистическую значимость.

Рассмотрим две непрерывные переменные x=(x₁, x₂,.., x_n), y=(y₁, y₂,..., y_n).

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова "регрессия" исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей "регрессировал" и "двигался вспять" к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины 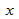остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

Между 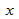и существует линейное соотношение: для любых пар 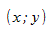данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

Остатки нормально распределены с нулевым средним значением;

Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от 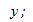мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать 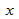или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Задание 2

Предполагается, что объем Y предложения некоторого товара зависит линейно от цены данного товара Х: y=a0+a1x+e. Статистические данные, собранные за T периодов, приведены в таблицах по вариантам. Требуется построить регрессионную модель Построение модели вести в следующей последовательности:

· Построить корреляционное поле

· Оценить параметры модели по методу наименьших квадратов

· Вычислить коэффициент детерминации R2

· Проверить, используя критерии Стьюдента и Фишера, адекватность линейной модели

· Установить с помощью статистики Дарбина – Уотсона (DW) наличие (отсутствие) автокорреляции

Данные: g=0,9 (a=0,1); T=10

t
x	4,4	12,9	5,5	15,5	13,9	15,3	14,2	11,2	5,5	10,8
y	2,6	10,9	6,2		16,1	14,7	11,1	12,7	6,2	8,4

Табличные значения для исследуемой зависимости (n=10, k₁=1, k₂=n-k-1=8):

Коэффициент Стьюдента, (t_табл)	1,86	При 90% надежности и K₂=8
Коэффициент Фишера-Синекдора, (F_табл)	3,46	K₁=1, K₂=8, a=0,1
Дарбин-Уотсон	Dн=0,88	Dв=1,32

Корреляционное поле:

Судя по графику, между х и у существует прямая зависимость (т.е. а₁>0). А а₀<0, т.к. пресечение прямой с осью у произойдет в области отрицательных значений у.

Обработка данных с помощью МНК:

Для расчетов была построена следующая таблица:

t	x	y	x*y	x^2	y^2	x-x_ср	(x-x_ср)^2
	4,4	2,6	11,44	19,36	6,76	-6,52	42,5104
	12,9	10,9	140,61	166,41	118,81	1,98	3,9204
	5,5	6,2	34,1	30,25	38,44	-5,42	29,3764
	15,5			240,25		4,58	20,9764
	13,9	16,1	223,79	193,21	259,21	2,98	8,8804
	15,3	14,7	224,91	234,09	216,09	4,38	19,1844
	14,2	11,1	157,62	201,64	123,21	3,28	10,7584
	11,2	12,7	142,24	125,44	161,29	0,28	0,0784
	5,5	6,2	34,1	30,25	38,44	-5,42	29,3764
	10,8	8,4	90,72	116,64	70,56	-0,12	0,0144
сумма	109,2	104,9	1307,53	1357,54	1288,81		165,076
среднее	10,92	10,49	130,753	135,754	128,881		16,5076

После проведения расчетов были получены данные:

xcp*ycp	114,5508
cov(x,y)	16,2022
var(x)	16,5076
var(y)	18,8409
b	0,981499
a	-0,22797
rxy	0,918716

Полученное линейное уравнение парной регрессии: y=0,98x-0,23

Значение коэффициента корреляции (rxy) близко к 1 (0,92), что говорит о достаточно высокой взаимосвязи переменных.

Остатки:

Для проверки на автокорреляцию строится таблица остатков e. Остатки – разность между эмпирическими Y и Y, полученными для тех же Х с помощью функции, полученной через МНК.

Фактический коэффициент Дарбина-Уотсона вычисляется по формуле:

где e – остатки. Далее с помощью табличных значений строятся интервалы:

Для нахождения коэффициента Дарбина-Уотсона строим таблицу:

y~	e	e^2	Еt-Еt-1	(Еt-Еt-1)^2
4,090624	-1,49062	2,221959
12,43337	-1,53337	2,35122	-0,04274516	0,0018271
5,170273	1,029727	1,060338	2,563095786	6,56946
14,98527	1,014733	1,029682	-0,014994306	0,0002248
13,41487	2,685132	7,209932	1,670399089	2,7902331
14,78897	-0,08897	0,007915	-2,774099203	7,6956264
13,70932	-2,60932	6,808541	-2,520350626	6,3521673
10,76482	1,93518	3,744922	4,544498292	20,652465
5,170273	1,029727	1,060338	-0,905453246	0,8198456
10,37222	-1,97222	3,889652	-3,001946982	9,0116857
сумма		29,3845		53,893535

С помощью полученных данных находим d=1,83. Теперь подставляем значение в таблицу для нахождения автокорреляции.

от 0 до 0,88		Положительная АК
от 0,88 до 1,32		Неопределенность
От 1,32 до 2,68	1,83	Отсутствие АК
от 2,68 до 3,12		Неопределенность
От 3,12 до 4		Отрицательная АК

Т.к. d находится в промежутке от 1,32 до 2,68, автокорреляция отсутствует. Это подтверждается также хаотичным характером знаков и упорядоченности остатков на графике:

12 3 Следующая ⇒

Воспользуйтесь поиском по сайту: