 |
Построение зависимости с помощью инструмента Анализ данных/регрессия
|
|
|
|
Полученное по МНК уравнение множественной регрессии с свободным членом:
y=2771378,25x1+0,673427899x2-814812,638x3+ 176458,043
| Регрессионная статистика | |
| Множественный R | 0,996262 |
| R-квадрат | 0,992538 |
| Нормированный R-квадрат | 0,990503 |
| Стандартная ошибка | 41827,65 |
| Наблюдения |
Коэффициенты корреляции и детерминации позволяют судить о высокой зависимости Y от рассматриваемых переменных. Предварительно модель справедлива и обоснована. Вместе с тем велика стандартная ошибка (что обусловлено величиной самих переменных).
Проверка значимости МНК-коэффициентов (Стьюдент)
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 125057,8 | 1,411012 | 0,185892 | |
| X1 | 224762,7 | 12,33024 | 8,8E-08 | |
| X2 | 0,673428 | 0,063128 | 10,66762 | 3,86E-07 |
| X3 | -814813 | -3,08818 | 0,01032 |
Значимость полученных коэффициентов проверяется сравнением фактического значения коэффициент Стьюдента (tстат) для каждого коэффициента и табличного для зависимости (1,80; 2,20; 2,72). Коэффициенты х1 и х2 значимы при всех трех уровнях точности, т.к. фактические значения больше табличных. А коэффициенты х3 и Y-пересечение – незначимы при всех уровнях точности, т.к. фактические значения меньше табличных.
Проверка значимости коэффициента детерминации (Критерий Фишера)
| df | SS | MS | F | Значимость F | |
| Регрессия | 2,56E+12 | 8,53E+11 | 487,7134 | 5,62198E-12 | |
| Остаток | 1,92E+10 | 1,75E+09 | |||
| Итого | 2,58E+12 |
Фактический коэффициент Фишера для полученного МНК-уравнения больше табличного коэффициента (3,59) для рассматриваемого вида зависимости. Это позволяет судить о статистической значимости коэффициента детерминации, а также о том, что уравнение сформировалось не случайно.
Доверительные интервалы:
|
|
|
| Предел. ошибка (D) | Нижняя граница | Верхняя граница | |
| х1 | 494477,8758 | 2276900,374 | |
| х2 | 0,138882085 | 0,534545814 | 0,81231 |
| х3 | 580467,8066 | -1395280,445 | -234345 |
| своб. член | 388207,6947 | -211749,6516 | 564665,7 |
Уравнение в интервальной форме:
у= (2771378,25±494477,8758)х1+(0,673427899±0,138882085)х2-(814812,638±580467,8066)х3+(176458,043±388207,6947), P=95%
Проверим модель на наличие автокорреляции:
| Наблюдение | Предск. Y | Остатки | е^2 | Et-Et-1 | (Et-Et-1)^2 |
| 141268,3 | 3898,659 | 15199544,16 | |||
| 167462,1 | 2729,948 | 7452613,785 | -1168,71 | 1365887,033 | |
| 252316,3 | -4810,34 | 23139380,06 | -7540,29 | 56855951,11 | |
| 337959,2 | -28568,2 | 816142171,8 | -23757,9 | 564435966,9 | |
| -13029 | 169755406,4 | 15539,18 | 241466127,8 | ||
| 374859,7 | -918,663 | 843941,056 | 12110,36 | 146660796,4 | |
| 416007,3 | 4907,739 | 24085899,12 | 5826,401 | 33946952,6 | |
| 460212,3 | 13804,73 | 190570432,7 | 8896,986 | 79156365,51 | |
| 473349,3 | 59240,67 | 45435,95 | |||
| 691235,5 | -14464,5 | 209223168,1 | -73705,2 | ||
| -81139 | -66674,5 | ||||
| -23970,5 | 57168,55 | ||||
| 83129,92 | 107100,4 | ||||
| -10656,8 | 113566749,2 | -93786,7 | |||
| 9845,401 | 96931926,59 | 20502,17 | 420339032,3 | ||
| сумма |
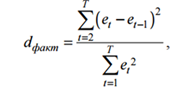d=1,923675252
| от 0 до 0,82 | Положительная АК | |
| от 0,82 до 1,75 | Неопределенность | |
| от 1,75 до 2,25 | 1,92 | Отсутствие АК |
| от 2,25 до 3,18 | Неопределенность | |
| от 3,18 до 4 | Отрицательная АК |
Автокорреляция отсутствует.
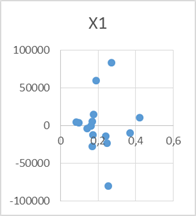
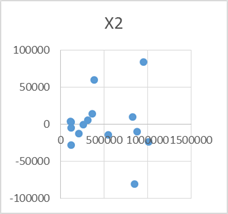
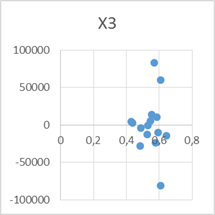
Графики остатков подкрепляют проведенное выше исследование модели на автокорреляцию.
Точечные графики предсказанных с помощью модели значений и значений из таблицы в зависимости от значений каждой независимой переменной модели:
х1 х2 х3
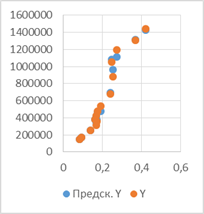
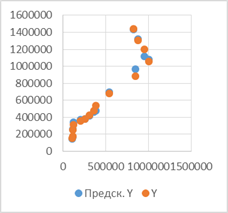
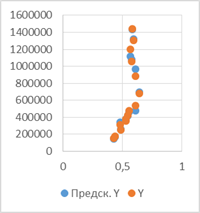
Полученная при помощи МНК зависимость у=(2771378,25±494477,8758)х1+
(0,673427899±0,138882085)х2-(814812,638±580467,8066)х3+(176458,043±388207,6947), P=95% не совершенна, есть недостатки, и их необходимо устранить для повышения ее эффективности и предсказательной силы. После внесения правок модель вполне может быть использована для прогнозов, обладая высокой точностью.
· Коэффициенты при одной переменной и свободном члене статистически не значимы и образовались случайно
· Коэффициент детерминации статистически значим, уравнение образовалось не случайно
|
|
|
· Автокорреляция отсутствует
Для повышения эффективности модели необходимо вывести все переменные кроме х1 и х2 из модели, или найти зависимости между переменными и выразить их через переменные х1 и х2, как наиболее значимые.
Список использованных источников
1. Линейная регрессия [Электронный ресурс]. – Режим доступа:http://www.statistica.ru/theory/osnovy-lineynoy-regressii/. – Дата доступа: 26.11.2015.
2. Википедия [Электронный ресурс]. – Режим доступа:https://ru.wikipedia.org. – Дата доступа: 26.11.2015.
3. Овсянникова М.М. Компьютерный практикум по эконометрике: Для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит», 080105 «Финансы и кредит». – Глазов: Глазовский инженерно-экономический институт, 2011. – 64 с.
|
|
|
