 |
Траектория движения жидкой частицы и линии тока
|
|
|
|
Линией тока называется кривая, обладающая тем свойством, что в данный момент времени векторы скоростей в любой ее точке совпадают по направлению с касательными.
В векторной форме это условие может быть записано как 
, т.е. векторное произведение должно быть равно нулю. Это, как известно (см. формулу 1.4), может быть записано в виде определителя
(4.7)
Раскрывая определитель, получаем дифференциальное уравнение линии тока в виде
(4.8)
Под траекторией понимается след, оставленный движущейся частицей в пространстве. Дифференциальное уравнение траектории
(4.9)
Из сопоставления (4.8) и (4.9) следует, что в общем случае, т.е. при неустановившемся движении, линии тока и траектории не совпадают.
Смоченый периметр и гидравлический радиус
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой c.
В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.
Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру c:
При напорном движении в трубе круглого сечения гидравлический радиус будет равен:
,
т.е. четверти диаметра, или половине радиуса трубы.
Для безнапорного потока прямоугольного сечения с размерами 
гидравлический радиус можно вычислить по формуле
.
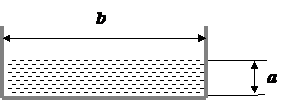
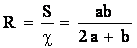Уравнение неразрывности и его физический смысл
При стационарном течении количество жидкости, втекающей в единицу времени в трубку тока через сечение 
, равно количеству жидкости, вытекающей через сечение 
(рис. 6.1). Если поперечное сечение трубки тока бесконечно мало, то можно считать, что скорость жидкости одинакова во всех точках одного и того же поперечного сечения. Масса жидкости, протекающая за время 
через поперечное сечение трубки, определяется выражением:
|
|
|
,
где 
– плотность жидкости, а S – площадь поперечного сечения трубки. В случае стационарного течения масса 
будет одной и той же для всех сечений трубки тока. Если взять два сечения, площади которых равны 
и 
, то можно написать:
.
Если бы это равенство не соблюдалось, то масса жидкости между сечениям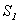и 
и 
изменялась бы во времени. А это противоречит закону сохранения массы и предположению о стационарности течения. Если жидкость несжимаема, то 
, и последнее соотношение принимает вид:
 .
| (6.1) |
Это соотношение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, то есть за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости. Скорость жидкости в одной и той же трубке тока больше там, где меньше площадь поперечного сечения трубки.
Уравнение Бернулли для идеальной и вязкой жидкости
Для идеальной
Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 
равна:
|
|
|
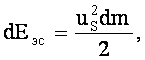
где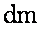 
- масса жидкости плотностью 
, протекающей через живое сечение элементарной струйки 
со скоростью 
за время dt, равная:
.
Проинтегрировав выражение для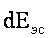 
, получим выражение для кинетической энергии потока идеальной жидкости 
.
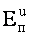Для вязкой
Перед тем, как записать уравнение Бернулли для потока вязкой жидкости необходимо оговорить два момента. Поток жидкости отличается от элементарной струйки тем, что он имеет реальные размеры поперечного сечения, которые могут быть довольно значительных размеров. Распределение давлений и скоростей по сечению потока может быть неравномерным.
Рассмотрим распределение давления. В плоскости перпендикулярной направлению движения, гидродинамическое давление распределяется по закону гидростатики. В связи с этим справедливо условие:
т.е. сумма отметки z и пьезометрической высоты 
во всех точках сечения потока остается одинаковой, хотя меняется для различных сечений.
В связи с тем, что распределение местных скоростей U в плоскости сечения потока неравномерно и в большинстве случаев неизвестно, то возникают трудности с определением кинетической энергии потока, т.е. с третьим слагаемым в уравнении Бернулли 
. Поэтому вводим корректирующий коэффициент ±, представляющий собой отношение действительной кинетической энергии потока к кинетической энергии, подсчитанной по средней скорости в сечении. Корректив ± называется коэффициентом кинетической энергии потока или коэффициентом Кориолиса, и отражает неравномерность распределения местных скоростей по сечению потока.
Для наиболее распространенных случаев движения жидкости значения ± следующее: при ламинарном движении в круглой трубе ± = 2, при турбулентном – зависит от режима и принимает значение ± = 1,1 
1,3. Обычно ± определяют опытным путем.
Коэффициент Кориолиса
Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии к кинетической энергии потока, вычисленной по средней скорости. Таким образом, поправочный коэффициент учитывает неравномерность скорости по живому сечению потока.
Коэффициент Кориолиса зависит от режима течения жидкости.
Для ламинарного режима = 2.
Для турбулентного режима = 1,13…1,15
|
|
|
|
|
|
