Графики Никурадзе и Мурина

Наиболее полные исследования по определению зависимости коэффициента l от числа Рейнольдса и от относительной шероховатости были выполнены И. Никурадзе.

И. Никурадзе испытал ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученных просеиванием через сита. Такая шероховатость называется равномерно зернистой. Испытания были проведены при широком диапазоне относительных шероховатостей , а также чисел Рейнольдса .

Данные опытов И. Никурадзе изобразил на графике, где по оси абсцисс откладывались логарифмы величин Re, а по оси ординат – логарифмы 100 l при различных значениях относитель­ных шероховатостей (рис. 6.6).

 

Рис. 6.6. График Никурадзе

 

При Re < 2300 (lg Re < 3,36) – прямая 1 – имеет место ламинарный режим и l зависит только от числа Рейнольдса и не зависит от шероховатости стенок.

При – участок 2 – наблюдается быстрый переход от ламинарного режима к турбулентному. Далее начинается прямая 3, характеризующая зависимость l от числа Рейнольдса для гидравлически «гладких» труб, у которых величина выступов шероховатостей меньше толщины ламинарной пристенной пленки. Далее кривые зависимости l от Re расходятся. Участки кривых 4 характеризуют собой переход от гидравлически «гладких» труб к гидравлически «шероховатым» трубам 5, т. е. в зоне 4 – 5 коэффициент гидравлического трения l зависит как от шероховатости, так и от Re.

Последняя область 5 представлена линиями, параллельными оси абсцисс, что свидетельствует о том, что здесь коэффициент гидравлического трения зависит только от шероховатости. Эту область обычно называют областью квадратичного сопротивления, так как потери напора по длине пропорциональны квадрату скорости.

Для труб с естественной шероховатостью закон изменения l от Re получается несколько иным, без подъема кривых после отклонения их от линии гладких труб. Различие объясняется тем, что в трубах с естественной шероховатостью выступы шероховатости имеют различную высоту и при увеличении числа Рейнольдса начинают выступать за пределы ламинарного слоя не одновременно, а при разных Re. Поэтому переход от линии «гладких» труб к горизонтальным прямым, соответствующим квадратичному закону, происходит более плавно, без провала кривых, что наглядно представлено на графике Г. А. Мурина (рис. 6.7).

 

 

Рис. 6.7. График Мурина

 

Простой трубопровод. Сложная система

Простым (коротким) называют трубопровод, по которому жидкость транспортируют от питателя к приемнику без промежуточных ответвлений потока. При этом необходимо учитывать не только потери напора на трение по длине трубопровода, но и скоростной напор и местные потери напора, которыми в данном случае нельзя пренебречь.

Исходным при расчетах простого трубопровода (рис.)

является уравнение баланса напоров (уравнение Бернулли)

Схема к расчету короткого трубопровода

Учитывая, что v²1/2g=0, Н1— H2= H; v2 = v1 и

получим

откуда средняя скорость истечения жидкости

Введем обозначение где j — коэффициент скорости, а

— коэффициент сопротивления системы

Следовательно, окончательно

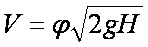
Расход жидкости, пропускаемой через короткий трубопровод, можно определить по формуле

где m=j — коэффициент расхода; S — площадь живого сечения.

Понятие короткого и длинного трубопроводов

Длинные трубопроводы

Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь.

Потери напора по длине трубопровода определяют

по формуле Дарси—Вейсбаха:

Учитывая, что расход Q = VЧS и скорость движения потока тогда

или

где А — удельное сопротивление трубопровода, определяемое по справочным таблицам;

Для переходной области удельное сопротивление Ао=А*b,

где b — поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения l от числа Рейнольдса.

Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубопроводов, базирующийся на формуле Шези.

Широко применяемые гидравлические параметры — это модуль расхода , сопротивление трубопровода ST=A*l, проводимость трубопровода . С помощью вышеуказанных параметров потери напора по длине можно определить следующим образом:

Короткие трубопроводы рассчитывают непосредственно по уравнению Бернулли с учетом потерь по длине и местных сопротивлений

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: