 |
Пространство элементарных исходов и алгебра случайных событий.
|
|
|
|
Выборка в задачах комбинаторики. Правило суммы и произведения.
Выборка объема R из n элементов – это (не) упорядоченный набор элементов ai1, ai2…air из исходного множества (элементы выборки могут повторяться).
Выборки элементов без повторений. Опр: Упорядоченная выборка объема n из n элементов называется перестановкой. Их числоPn находится по формуле 
Опр: Упорядоченная выборка объема m из n элементов (m<=n) называется размещением.
Число размещений из n элементов по m обозначим 
Опр: Неупорядоченная выборка объема из n элементов (m<=n) называется сочетанием. Число 
таких сочетаний находится 
Выборки элементов с повторениями. Опр:Упорядоченная выборка объема mиз nэлементов где элементы могут повторяться называется размещение с повторением. 
Опр: Из nэлементов пусть К1 – элементы 1 сорта, К2 – 2го сорта, Kr – rсорта. К1+К2+… +Kr=n. Упорядоченная выборка объема nиз nэлементов (с повторением) называется перестановкой с повторениеми. 
Опр: Пусть имеется nтипов элементов, каждый тип содержит не менее mодинаковых элементов. Неупорядоченная выборка объема mиз всех имеющихся элементов называется сочетанием с повторениями, их число обозначается 
Правило произведения. Если объектА можно выбрать mспособами, а объект В n-способами, то одновременный выбор А и В, m*nспособов
Правило суммы. Если объектА можно выбрать mспособами, а объект В n-способами, и если одновременный выбор А и В невозможен, то выбор А и В можно осуществить m+nспособами.
Перестановки, размещения, сочетания и их количество.
Формула расчета количества перестановок. Перестановками называются комбинации, состоящие из одних и тех же n-различных исходный элементов и отличающиеся только порядком расположения элементов. Число возможных перестановок:Рn=n!
|
|
|
Формула расчета количества размещений. Размещениями называют комбинации, составленные из n-различных исходных элементов по mэлементов в каждой комбинации, отличающихся либо составом элементов, либо их порядком. Число возможных размещений: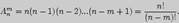 
Формула расчета количества сочетаний. Сочетаниями называют комбинации, составленные из n-различных исходных элементов по mпозиций, отличающиеся хотя бы одним элементом. Число возможных сочетаний: 
. Данные формулы справедливы только для выборок с неповторяющимися исходными элементами.
Число перестановок, размещений, и сочетаний с повторениями.
Выборки элементов с повторениями. Опр:Упорядоченная выборка объема mиз nэлементов где элементы могут повторяться называется размещение с повторением. 
Опр: Из nэлементов пусть К1 – элементы 1 сорта, К2 – 2го сорта, Kr – rсорта. К1+К2+… +Kr=n. Упорядоченная выборка объема nиз nэлементов (с повторением) называется перестановкой с повторениеми.
Опр: Пусть имеется nтипов элементов, каждый тип содержит не менее mодинаковых элементов. Неупорядоченная выборка объема mиз всех имеющихся элементов называется сочетанием с повторениями, их число обозначается 
Пространство элементарных исходов и алгебра случайных событий.
Пространство элементарных событий — множество 
всех различных исходов случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой 
(«омега») с индексами или без. 
Событие называется достоверным, если оно происходит при любом испытании. Достоверное событие обозначается символом Ω.Событие называется невозможным, если оно не происходит при любом испытании. Невозможное событие обозначим символом Ø.
Алгебра событий (в теории вероятностей) — алгебра подмножеств пространства элементарных событий 
, элементами которого служат элементарные события.
|
|
|
Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В.События А и В называются несовместными событиями, если не существует элементарных исходов, принадлежащих подмножествам А и В одновременно. Другими словами, события А и В несовместны, если их одновременное появление невозможно, т.е. 
. В противном случае события и называют совместными.
Р(А+В)=Р(А)+Р(В)-Р(АВ) – если А и В совместны.
Для несовместных событий Р(А+В)=Р(А)+Р(В)
А\В - Iпринадлежит А и не принадлежит В
Противоположным к событию А называется событие 
, состоящее в том, что событие А в результате эксперимента не произошло. Иначе говоря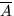 
, есть множество, содержащее элементарные исходы, не входящие в А.
Р(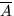)=1-Р(А).
Правила:
1)А*А=А, 2) А+А=А, 3) А* 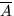= , 4) А+В с черточкой на верху=А черточка на верху*В черточка наверху, 5) (А+В)*С=АС+ВС, 6)А+В=А+В 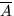, 7) В= 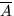В+АВ
Р(А+В)=Р(А)+Р(В 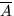); Р(В)=Р( 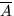В)+Р(АВ).
|
|
|
