 |
Доверительный интервал. Методы его построения.
|
|
|
|
Доверительный интервал - термин, используемый в математической статистике при интервальной оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Определение. Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100 p%, порождённым выборкой (x 1,…, x n), называется интервал с границами 
(x 1,…, x n) и 
(x 1,…, x n), которые являются реализациями случайных величин L (X 1,…, X n) и U (X 1,…, X n), таких, что 
.
Граничные точки доверительного интервала 
и 
называются доверительными пределами.
Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.
СРОТКЛ Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего.
СРЗНАЧ Возвращает среднее арифметическое аргументов.
БИНОМРАСП Возвращает отдельное значение биномиального распределения.
ХИ2РАСП Возвращает одностороннюю вероятность распределения хи-квадрат.
ХИ2ОБР Возвращает обратное значение односторонней вероятности распределения хи-квадрат.
ХИ2ТЕСТ Возвращает тест на независимость.
ДОВЕРИТ Возвращает доверительный интервал для среднего значения по генеральной совокупности.
КОРРЕЛ Возвращает коэффициент корреляции между двумя множествами данных.
КОВАР Возвращает ковариацию, среднее произведений парных отклонений
КВАДРОТКЛ Возвращает сумму квадратов отклонений.
FРАСП Возвращает F-распределение вероятности.
FРАСПОБР Возвращает обратное значение для F-распределения вероятности.
|
|
|
ЧАСТОТА Возвращает распределение частот в виде вертикального массива.
ЭКСЦЕСС Возвращает эксцесс множества данных.
ЛИНЕЙН Возвращает параметры линейного тренда.
МОДА Возвращает значение моды множества данных.
НОРМРАСП Возвращает нормальную функцию распределения.
НОРМОБР Возвращает обратное нормальное распределение.
НОРМСТОБР Возвращает обратное значение стандартного нормального распределения.
СКОС Возвращает асимметрию распределения.
НАКЛОН Возвращает наклон линии линейной регрессии.
СТАНДОТКЛОН Оценивает стандартное отклонение по выборке.
СТАНДОТКЛОНА Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения.
СТОШYX Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии.
СТЬЮДРАСП Возвращает t-распределение Стьюдента.
СТЬЮДРАСПОБР Возвращает обратное t-распределение Стьюдента.
ДИСП Оценивает дисперсию по выборке.
ДИСПА Оценивает дисперсию по выборке, включая числа, текст и логические значения.
ДИСПР Вычисляет дисперсию для генеральной совокупности.
ДИСПРА Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения.
ZТЕСТ Возвращает двустороннее P-значение z-теста.
29.Проверка гипотез. Хи-квадрат. В эксель…
Критерий 
- статистический критерий для проверки гипотезы 
, что наблюдаемая случайная величина подчиняется некому теоретическому закону распределения.
Определение
Пусть дана случайная величина X.
Гипотеза 
: с. в. X подчиняется закону распределения 
.
Для проверки гипотезы рассмотрим выборку, состоящую из n независимых наблюдений над с.в. X: 
. По выборке построим эмпирическое распределение 
с.в X. Сравнение эмпирического 
и теоретического распределения (предполагаемого в гипотезе) производится с помощью специально подобранной функции — критерия согласия. Рассмотрим критерий согласия Пирсона (критерий 
):
|
|
|
Гипотеза 
: Хn порождается функцией .
Разделим [a,b] на k непересекающихся интервалов 
;
Пусть 
- количество наблюдений в j-м интервале: 
;
- вероятность попадания наблюдения в j-ый интервал при выполнении гипотезы 
;
- ожидаемое число попаданий в j-ый интервал;
Статистика: 
- Распределение хи-квадрат с k-1 степенью свободы.
Проверка гипотезы 
В зависимости от значения критерия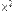 
, гипотеза может приниматься, либо отвергаться:
, гипотеза 
выполняется.
(попадает в левый "хвост" распределения). Следовательно, теоретические и практические значения очень близки. Если, к примеру, происходит проверка генератора случайных чисел, который сгенерировал n чисел из отрезка [0,1] и гипотеза 
: выборка 
распределена равномерно на [0,1], тогда генератор нельзя называть случайным (гипотеза случайности не выполняется), т.к. выборка распределена слишком равномерно, но гипотеза выполняется.
(попадает в правый "хвост" распределения) гипотеза отвергается.
ХИ2ОБР 
Скрыть все -возвращает значение, обратное односторонней вероятности распределения хи-квадрат.
ХИ2РАСП - в Скрыть все
в вввв озвращает одностороннюю вероятность распределения хи-квадрат.
ХИ2ТЕСТ Скрыть все - возвращает критерий независимости.
|
|
|
