 |
Увеличение числа испытаний. Закон Пуассона.
|
|
|
|
Распределение Пуассона - вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Событие называются редкими, когда вероятность события р или противоположного ему q близка к нулю. При большом числе испытаний (n), но небольшой величине произведения числа испытаний на вероятность (np),
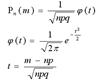
которое меньше 10, вероятности полученные по формуле Лапласа
недостаточно близки к их истинным значениям. Тогда применяют другую асимптотическую формулу Пуассона.
Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, произведение np = λ, то вероятность Рn(m) того, что в n независимых испытаниях события А наступит m раз, приближенно равна 
, т.е. 
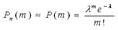
Свойства распределения Пуассона:
Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть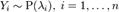 
. Тогда 
.
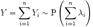Пусть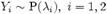 
, и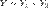 
. Тогда условное распределение 
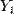при условии, что 
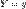, биномиально. Более точно: 
.
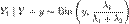12. Рост числа успехов? Локальная теорема Муавра-Лапласа
Теорема Муавра - Лапласа -одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.
При рассмотрении количества 
появлений события 
в 
испытаниях Бернулли чаще всего нужно найти вероятность того, что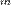 
заключено между некоторыми значениями a и 
. Так как при достаточно больших n промежуток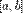 
содержит большое число единиц, то непосредственное использование биномиального распределения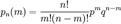 
|
|
|
требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей.
Поэтому используют асимптотическое выражение для биномиального распределения при условии, что 
фиксированно, а 
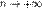. Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция.
Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина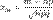 
ограничена равномерно по m и n 
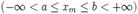, то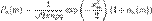 
где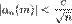 
, c > 0, c — постоянная.
Интегральная теорема Лапласа. Кривая Гаусса.
Теорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна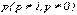 
. Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, 
.
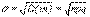Следствия из интегральной теоремы Муавра-Лапласа
Пусть выполнены условия применимости интегральной теоремы Муавра-Лапласа.
Следствие 1. Вероятность того, что число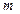 
наступлений события А в n повторных независимых испытаниях будет отличаться от величины 
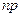не более чем на 
(по абсолютной величине), вычисляется по формуле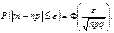 
Следствие 2. Вероятность того, что доля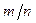 
наступлений события А в n повторных независимых испытаниях будет отличаться от вероятности p наступления этого события в одном испытании не более чем на 
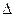(по абсолютной величине), вычисляется по формуле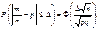 
Кривая Гаусса.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью
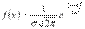. Нормальное распределение задается двумя параметрами: a – математическим ожиданием, 
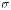– средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Нормированным называют нормальное распределение с параметрами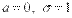 
.
Плотность нормированного распределения задается формулой
.
|
|
|
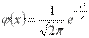Свойства. Если случайные величины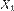 
и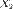 
независимы и имеют нормальное распределение с математическими ожиданиям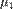и 
и 
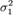и дисперсиями 
и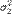 
соответственно, то 
также имеет нормальное распределение с математическим ожиданием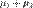 
и дисперсией 
.
|
|
|
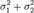