 |
Далее теорема не давалась. Привожу для полной картины.
|
|
|
|







[3] Площадь поверхности вращения



http://glaznev.sibcity.ru/1kurs/integr/htm_3/in_lek11.htm
 ,
, 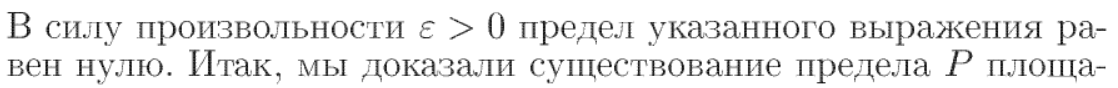

http://nuclphys.sinp.msu.ru/mathan/p2/m2804.html
[4] Замена переменных в определенном интеграле и интегрирование по частям





[4] Несобственные интегралы
Бывают двух видов:
1. С бесконечными пределами интегрирования – это НИ первого рода
2. НИ от неограниченных функций – это НИ второго рода
[4] Понятие несобственного интеграла первого рода



[4] Критерий Коши сходимости несобственного интеграла первого рода. Достаточные признаки сходимости.
НАЧАЛО НЕ ОБЯЗАТЕЛЬНОГО (НЕ ДАВАЛОСЬ НА ЛЕКЦИИ)





КОНЕЦ НЕ ОБЯЗАТЕЛЬНОГО (НЕ ДАВАЛОСЬ НА ЛЕКЦИИ)
[4] Абсолютная и условная сходимость несобственных интегралов








[4] Замена переменных под знаком несобственного интеграла и формула интегрирования по частям



[4] Несобственные интегралы второго рода
Определение, как свести к НИ 1-го рода







[5] Несобственные интегралы от неотрицательных функций

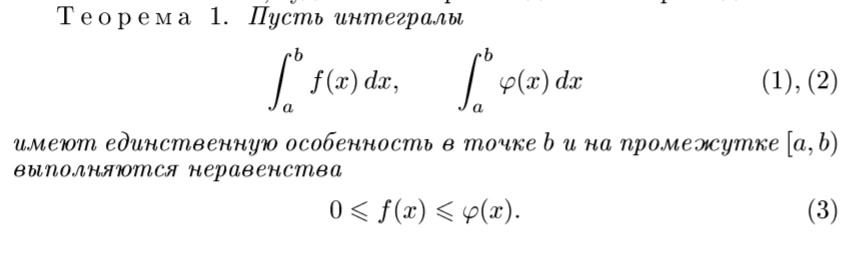


То же самое, но менее понятно, как по мне

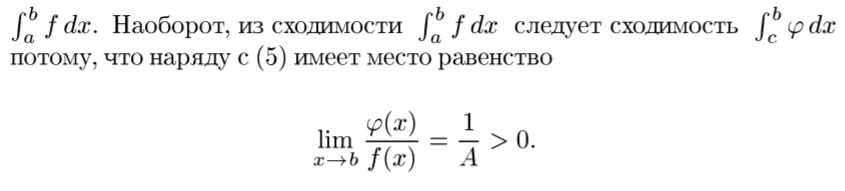

[5] Теория числовых рядов
[5] Критерий Коши сходимости ряда



Ниже необходимое условие сходимости. В ИП доказательство мне не понятно. Ниже приведено более понятное доказательство.




[5] Понятие числового ряда


[5] Два свойства, связанные со сходимостью ряда


[5] Ряды с положительными членами
[5] Необходимое и достаточное условие сходимости ряда с положительными членами


[5] Признаки сравнения




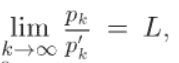



[5] Признаки Даламбера и Коши














[6] Интегральный признак Коши-Маклорена



Сначала не очень понятно. Так как f(k) и f(k-1) константы, то интеграл от них равен площади прямоугольника для f(k-1): прямоугольник с высотой f(k-1) и основанием k – (k-1) = 1 (промежуток интегрирования)
|
|
|
Аналогично для f(k): высота f(k) и основание 1.
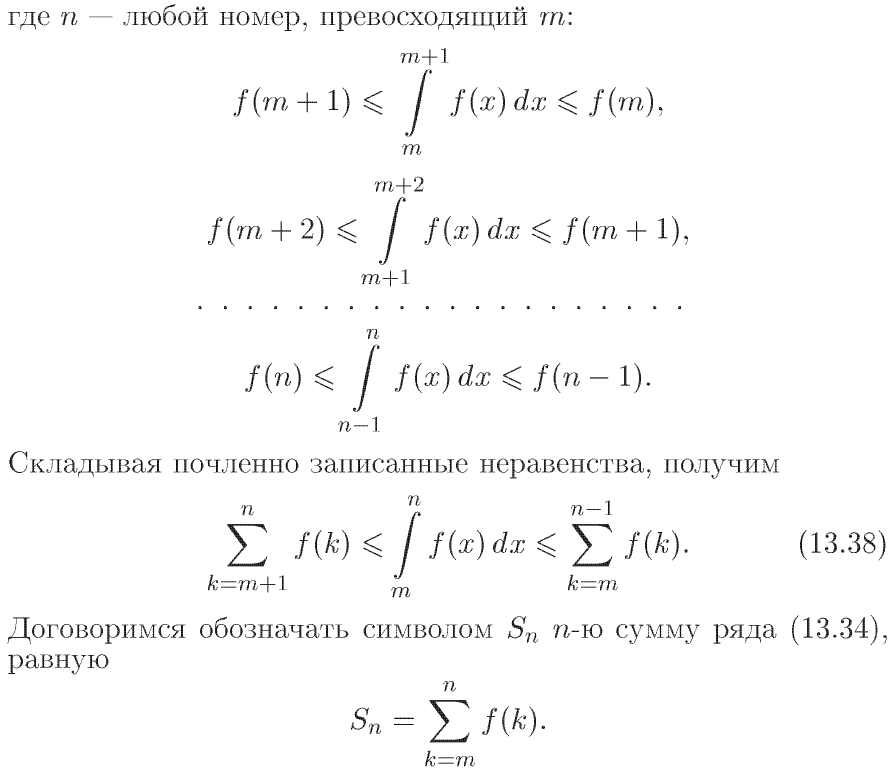






[6] Абсолютно и условно сходящиеся ряды
[6] Понятие абсолютно и условно сходящегося ряда





[6] Перестановка членов условно сходящегося ряда
НАЧАЛО НЕ ДАВАЛОСЬ НА ЛЕКЦИИ






[6] Перестановка членов абсолютно сходящегося ряда





КОНЕЦ НЕ ДАВАЛОСЬ НА ЛЕКЦИИ
[6] Признаки сходимости произвольных рядов



[6] Признак Лейбница (Знакочередующиеся ряды)



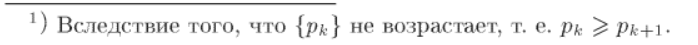

Вот это 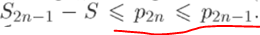 верно, т.к p2n<=p2n-1 по условию (т.к. ряд из модулей монотонно убывает). Соответственно если S2n-1 – S меньше p2n, то тем более она будет меньше числа, которое больше чем p2n.
верно, т.к p2n<=p2n-1 по условию (т.к. ряд из модулей монотонно убывает). Соответственно если S2n-1 – S меньше p2n, то тем более она будет меньше числа, которое больше чем p2n.
13.80 можно описать так: Остаток ряда Лейбница не превышает последнего члена остающейся частичной суммы

Альтернативное доказательство про остаток ряда



ЗАМЕЧАНИЕ: Остаток ряда Лейбница не превышает последнего члена остающейся частичной суммы.

[6] Функциональные ряды
[6] Понятие функциональной последовательности и функционального ряда

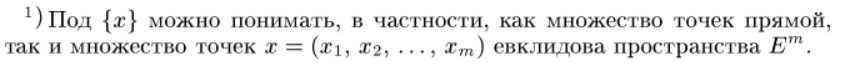


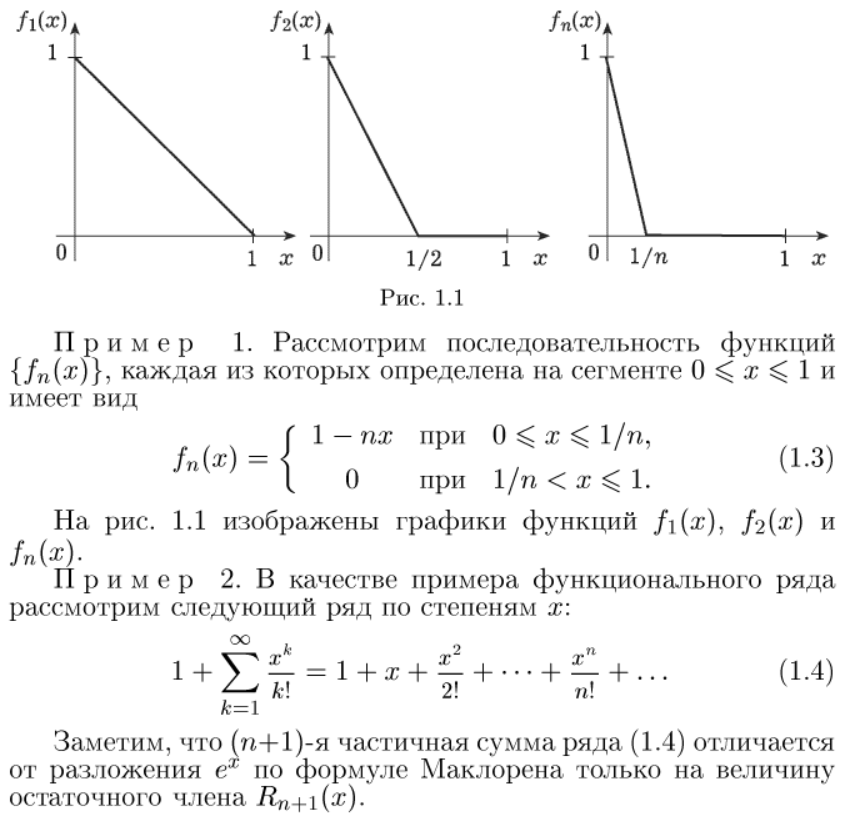
[6] Сходимость функциональной последовательности в точке и на множестве
Поточечная сходимость, область сходимости, предельная функция последовательности





[6] Понятие равномерной сходимости на множестве







[6] Некоторые свойства равномерно сходящихся рядов

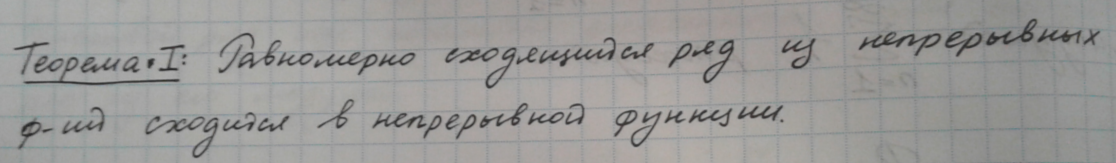


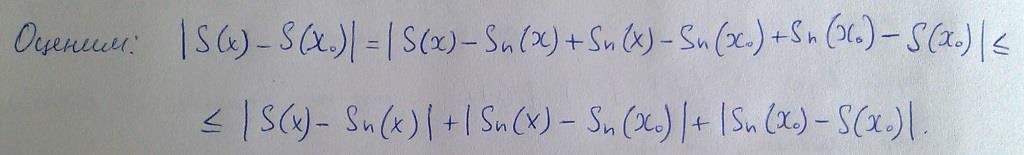

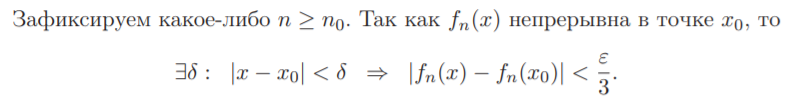
Теорема 2

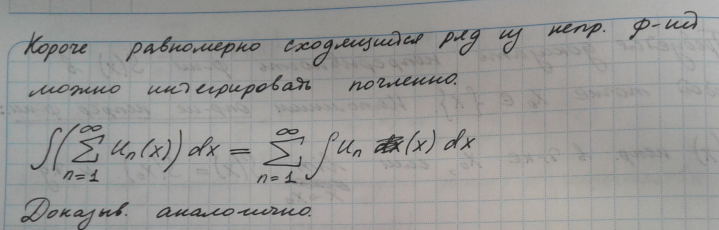
То же самое в учебнике:





Теорема 3. (Давалась без доказательства)


[7] Степенные ряды
[7] Степенной ряд и область его сходимости


НАЧАЛО НЕОБЯЗАТЕЛЬНОГО




КОНЕЦ НЕОБЯЗАТЕЛЬНОГО
[7] Теорема Абеля и радиус сходимости (тетрадь)
Радиус сходимости, промежуток сходимости ряда, формула радиуса сходимости
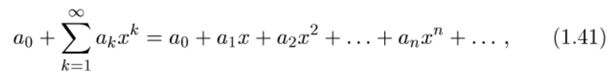



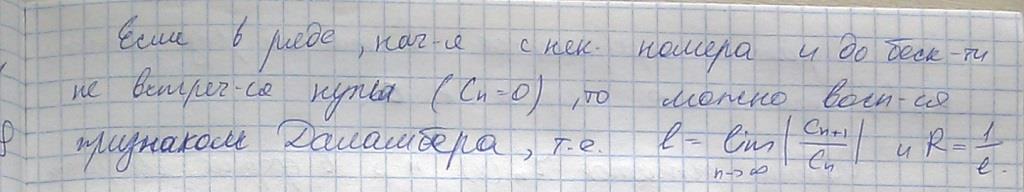
[7] Непрерывность суммы степенного ряда
Не давалось
|
|
|








Конец необязательного
[7] Свойства степенных рядов
БЕЗ ДОКАЗАТЕЛЬСТВ



[7] Разложение функций в степенной ряд





Доказательство утверждения 4

[7] Разложение некоторых элементарных функций в степенные ряды




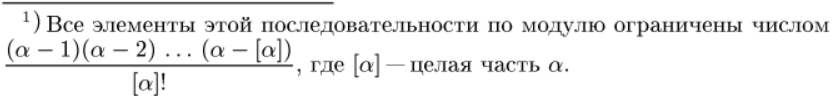

[7] Функции нескольких переменных
[7] Понятие евклидовой плоскости и евклидова пространства
Координатная плоскость, евклидова плоскость, координатное пространство, евклидово пространство

Два элемента a и b называются упорядоченной парой, если указано, какой из этих элементов первый, какой второй


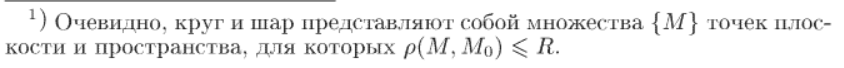
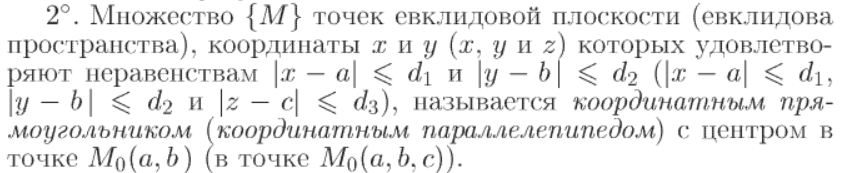
[7] Понятие функции двух и трех переменных


[7] Понятие m-мерного координатного пространства и m-мерного евклидова пространства




[7] Множества точек m-мерного евклидова пространства Em
m-мерный шар радиуса R, c центром в точке M0; открытый шар; m-мерная сфера радиуса R, c центром в точке M0; m-мерный координатный параллепипед, c центром в точке M0; Открытый параллепипед; E-окрестность точки в m-мерном евклидовом пространстве;
Внутренняя точка, граничная точка, открытое множество, замкнутое множество, связное множество



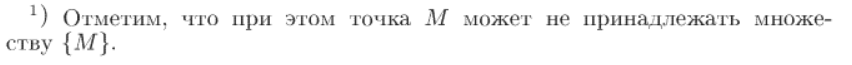


[7] Понятие функции m-переменных


[8] Предельное значение функции нескольких переменных
[8] Сходящиеся последовательности точек в m-мерном евклидовом пространстве. Критерий Коши сходимости последовательности



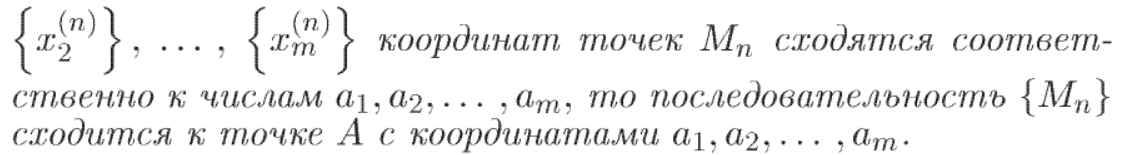
ЛЕММА 1 НЕ ДАВАЛАСЬ


ДАЛЕЕ НЕ ДАВАЛОСЬ ВВИДУ АНАЛОГИИ С ДВУМЕРНЫМ СЛУЧАЕМ


[8] Понятие предельного значения функции нескольких переменных

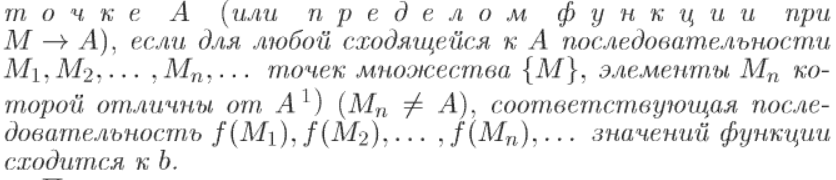




[8] Бесконечно малые функции
НАЧАЛО ТОГО, ЧТО НЕ ДАВАЛОСЬ

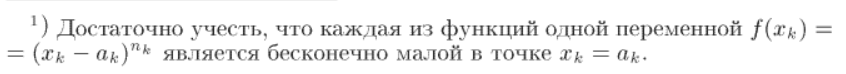
[8] Необходимое и достаточное условие существования предельного значения функции (критерий Коши)


[8] Повторные предельные значения



КОНЕЦ ТОГО, ЧТО НЕ ДАВАЛОСЬ
[8] Непрерывные функции нескольких переменных
[8] Определение непрерывности функции нескольких переменных









[8] Основные свойства непрерывных функций нескольких переменных



ДАЛЕЕ НЕ ДАВЛОСЬ, НО НЕПЛОХО ЭТО ПОНИМАТЬ





КОНЕЦ ТОГО, ЧТО НЕ ДАВАЛОСЬ
[9] Производные и дифференциалы функции нескольких переменных
[9] Частные производные функции нескольких переменных
Превью







|
|
|
[9] Понятие дифференцируемости функции нескольких переменных




То есть, если b = o (a) => b/a = 0, если наоборот a/b = бесконечности.
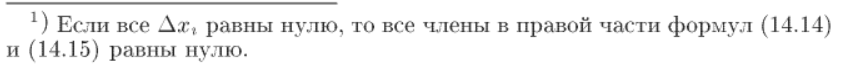


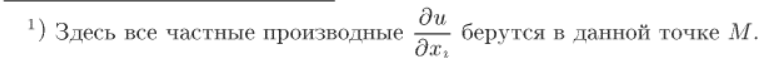
|
|
|


