 |
Уравнения с разделяющимися переменными
|
|
|
|
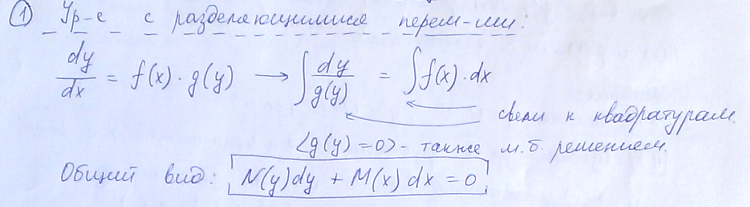30. Понятие квадратур обыкновенного дифференциального уравнения. Общий интеграл уравнения. Общее решение. Интегрирование однородного уравнения первого порядка.
Понятие квадратур обыкновенного дифференциального уравнения
Выражение общего решения или полного интеграла через элементарные функции и интегралы от них называют интегрированием данного ОДУ в квадратурах (термин "квадратура" в данной ситуации означает взятие неопределенного интеграла, а "интегрирование" — нахождение полного интеграла).
Интегрирование в квадратурах допускают лишь уравнения некоторых простейших типов. Большинство же ОДУ можно решать только приближенно или исследовать их качественными методами, то есть методами, позволяющими выяснять свойства решений без явного их отыскания. Качественные и приближенные методы составляют основное содержание современной теории обыкновенных дифференциальных уравнений.
Общий интеграл уравнения
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения.
Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения.
Более подробно и сложнее:
Общее решение.
Общее решение может быть представлено в виде общего интеграла (когда решение дано в виде неявной функции)или функции (когда решение представлено в виде явной функции).
Общим решением является функция вида:
Интегрирование однородного уравнения первого порядка
Общий вид можно записать так:
|
|
|
Пункт 3.2 а – это мы находим точку пересечения прямых, чтобы в нее перенести начало координат системы в пункте 3.2 б.
Случай 3.3 – когда указанные прямы параллельны.
Линейное дифференциальное уравнение первого порядка. Нахождение его решения. Метод вариации постоянной.
Линейное дифференциальное уравнение первого порядка.
Метод вариации постоянной.
Уравнение Бернулли. Уравнение в полных дифференциалах.
Уравнение Бернулли.
Уравнение в полных дифференциалах
Интегрирующий множитель. Доказательство его существования. Общий вид интегрирующего множителя. Примеры нахождения интегрирующего множителя.
Интегрирующий множитель
(это уравнение, похоже на уравнение в полных дифференциалах, но не выполняется условия равенства смешанных производных второго порядка)
Доказательство его существования
Общий вид интегрирующего множителя.
(из Еругин Н. П. Книга для чтения по общему курсу дифференциальных уравнений с. 93)
Если мы догадались до двух интегрирующих множителей µ0 и µ1, то µ1/ µ0 = C – есть решение д.у.
Примеры нахождения интегрирующего множителя.
Пример метода последовательного выделение полного дифференциала https://1cov-edu.ru/differentsialnye-uravneniya/integriruyuschii_mnozhitel/
Дифференциальные уравнения первого порядка, не разрешенные относительно производной. Метод введения параметра.
Случай 3
Уравнение Лагранжа
Уравнение Клеро
Уравнения высшего порядка, допускающие понижение порядка.
Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Нахождение общего решения в случае n различных действительных корней, в случае кратного корня и в случае комплексных корней.
Общие понятия
Из учебника «Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного» Бугров, Никольский
|
|
|
Это доказывается тем, что L[y] есть линейный оператор, а по его свойствам:
|
|
|
