 |
Необходимое условие дифференцируемости функции в точке
|
|
|
|







[9] Понятие дифференциала функции нескольких переменных


[9] Дифференцирование сложной функции






Далее не давалось


Более подробно смотри Фихтенгольц курс диф и инт исчисления том 1 стр 399.
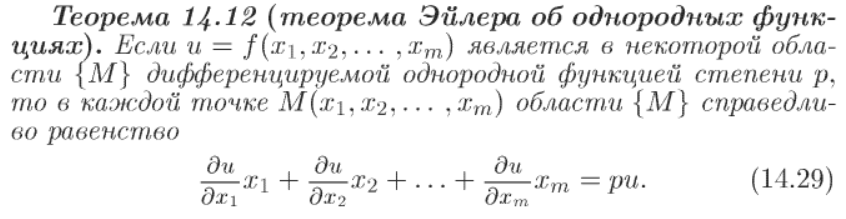


Конец того, что не давалось
[10] Инвариантность формы первого дифференциала







[10] Производная по направлению. Градиент. Поверхности уровня




Альтернативная формулировка определения




Более подробно про поверхности уровня






[10] Частные производные и дифференциалы высших порядков
[10] Частные производные высших порядков
Понятие частной производной второго и n-го порядков, понятие n раз дифференцируемой функции, теорема о порядке дифференцируемости.








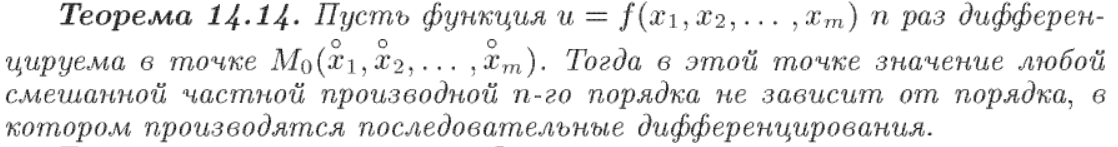

[10] Дифференциалы высших порядков
















[11] Формула Тейлора для функции m переменных с остаточным членов в форме Лагранжа






[11] Локальный экстремум функции m переменных
[11] Понятие экстремума функции m переменных. Необходимые условия локального экстремума





[11] Достаточные условия локального экстремума
Случай функции m-переменных
НЕ ДАВАЛОСЬ ДЛЯ ФУНКЦИИ M-Переменных. Нам давали только для частного случая, когда функция зависит только от двух переменных. Это будет ниже. Сейчас пойдет необязательное (общий случай)




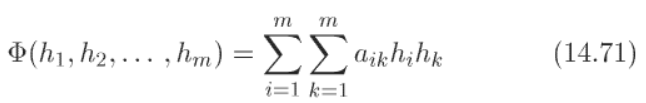
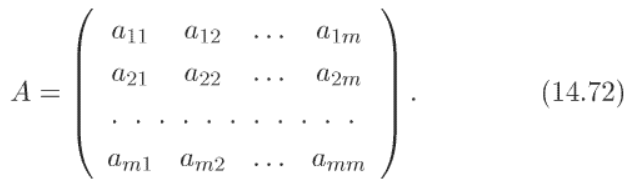

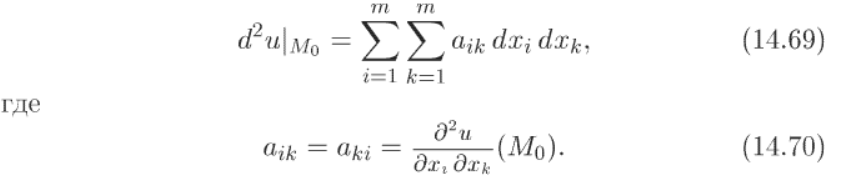
Доказательство на четыре страницы не привожу. Ильин-Позняк Матан том 1 стр 536 – 540.


Конец необязательного
Случай функции двух переменных


PS: В учебнике приводится другая формулировка и другое доказательство с опорой на теорему, которая нам не давалась. Поэтому привожу здесь формулировку из тетради.
|
|
|

Последняя строка выше. В разложении по Тейлору нет первого дифференциала, т.к. он по необходимому условию экстремума функции равен нулю.

[12] Обыкновенные дифференциальные уравнения
Взято из справочника по высшей математике М. Я. Выгодского




В общем, если ответ дан в виде x*y=0,2, то говорят, что это уравнение есть решение дифура или это уравнение есть интеграл дифура. А если явно выражается Y через X, т.е. y=0,2 / x, то говорят, что эта функция есть решение дифура.












Остальная информация доступно и примерами дана вот тут
http://www.math24.ru/%D1%81%D0%BE%D0%B4%D0%B5%D1%80%D0%B6%D0%B0%D0%BD%D0%B8%D0%B5-%D0%BE%D0%B1%D1%8B%D0%BA%D0%BD%D0%BE%D0%B2%D0%B5%D0%BD%D0%BD%D1%8B%D0%B5-%D0%B4%D0%B8%D1%84%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5-%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F.html
Вот список тем, которые нам читались. Где минус – то не давалось

Если что-то неясно, то гуглим, в лекциях давалось менее подробно, чем тут.
Понятие обыкновенного дифференциального уравнения. Задача Коши. Интегральная кривая. Уравнения с разделяющимися переменными.
Понятие обыкновенного дифференциального уравнения



В общем, если ответ дан в виде x*y=0,2, то говорят, что это уравнение есть решение дифура или это уравнение есть интеграл дифура. А если явно выражается Y через X, т.е. y=0,2 / x, то говорят, что эта функция есть решение дифура.
Задача Коши

Что бы решить задачу Коши – нужно получить общее решение дифференциального уравнения в которое входят произвольные постоянные. Далее нужно подставить в общее решение начальные условия (x0, y0) и найти константу C. Общее решение, в котором вместо С будет стоять найденное значение и есть частное решение дифференциального уравнение (а также решение задачи Коши).
Интегральная кривая
Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.


Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
|
|
|
|
|
|


