 |
Марковские цепи с конечным числом состояний и дискретным временем
|
|
|
|
Содержание
Введение........................................................................................................... 3
1 Марковские цепи с конечным числом состояний и дискретным временем 4
2 Марковские цепи с конечным числом состояний и непрерывным временем 8
3 Процессы рождения и гибели.................................................................... 11
4 Основные понятия и классификация систем массового обслуживания... 14
5 Основные типы открытых систем массового обслуживания.................... 20
5.1 Одноканальная система массового обслуживания с отказами.............. 20
5.2 Многоканальная система массового обслуживания с отказами........... 21
5.3 Одноканальная система массового обслуживания с ограниченной длиной очереди........................................................................................................................ 23
5.4 Одноканальная система массового обслуживания с неограниченной очередью........................................................................................................................ 26
5.5 Многоканальная система массового обслуживания с ограниченной очередью........................................................................................................................ 27
5.6 Многоканальная система массового обслуживания с неограниченной очередью........................................................................................................................ 30
5.7 Многоканальная система массового обслуживания с ограниченной очередью и ограниченным временем ожидания в очереди............................................. 32
6 Метод Монте-Карло................................................................................... 36
6.1 Основная идея метода............................................................................. 36
6.2 Разыгрывание непрерывной случайной величины................................ 36
6.3 Случайная величина с экспоненциальным распределением................. 38
7 Исследование системы массового обслуживания..................................... 40
|
|
|
7.1 Проверка гипотезы о показательном распределении............................ 40
7.2 Расчет основных показателей системы массового обслуживания........ 45
7.3 Выводы о работе исследуемой СМО..................................................... 50
8 Исследование видоизмененной СМО........................................................ 51
Заключение.................................................................................................... 53
Список использованных источников............................................................ 54
Введение
Темой моей дипломной работы является исследование системы массового обслуживания. В своем изначальном состоянии рассматриваемая мной СМО представляет собой один из классических случаев, а конкретно M/M/2/5 по принятому обозначению Кэндалла. После исследования системы были сделаны выводы о неэффективности ее работы. Были предложены методы оптимизации работы СМО, но с этими изменениями система перестает быть классической. Основная проблема при исследовании систем массового обслуживания заключается в том, что в реальности они могут быть исследованы с использованием классической теории массового обслуживания только в редких случаях. Потоки входящих и исходящих заявок могут оказаться не простейшими, следовательно, нахождение предельных вероятностей состояний с использованием системы дифференциальных уравнений Колмогорова невозможно, в системе могут присутствовать приоритетные классы, тогда расчет основных показателей СМО также невозможен.
Для оптимизации работы СМО была введена система из двух приоритетных классов и увеличено число обслуживающих каналов. В таком случае целесообразно применить методы имитационного моделирования, например метод Монте-Карло. Основная идея метода заключается в том, что вместо неизвестной случайной величины принимается ее математическое ожидание в достаточно большой серии испытаний. Производится разыгрывание случайной величины (в данном случае это интенсивности входящего и исходящего потоков) изначально равномерно распределенной. Затем осуществляется переход от равномерного распределения к показательному распределению, посредством формул перехода. Была написана программа на языке Visual Basic, реализующая этот метод.
|
|
|
Марковские цепи с конечным числом состояний и дискретным временем
Пусть некоторая система S может находиться в одном из состояний конечного (или счетного) множества возможных состояний S1, S2,…, Sn, а переход из одного состояния в другое возможен только в определенные дискретные моменты времени t1, t2, t3, называемые шагами.
Если система переходит из одного состояния в другое случайно, то говорят, что имеет место случайный процесс с дискретным временем.
Случайный процесс называется марковским, если вероятность перехода из любого состояния Si в любое состояние Sj не зависит от того, как и когда система S попала в состояние Si (т.е. в системе S отсутствует последствие). В таком случае говорят, что функционирование системы S описывается дискретной цепью Маркова.
Переходы системы S в различные состояния удобно изображать с помощью графа состояний (рис. 1).
Рисунок 1 – Пример размеченного графа состояний
Вершины графа S1, S2, S3 обозначают возможные состояния системы. Стрелка, направленная из вершины Si в вершину Sj обозначает переход 
; число, стоящее рядом со стрелкой, обозначает величину вероятности этого перехода. Стрелка, замыкающаяся на i-той вершине графа, обозначает, что система остается в состоянии Si с вероятностью, стоящей у стрелки.
Графу системы, содержащему n вершин, можно поставить в соответствие матрицу NxN, элементами которой являются вероятности переходов pij между вершинами графа. Например, граф на рис. 1 описывается матрицей P:
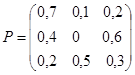
называемой матрицей вероятностей переходов. Элементы матрицы pij удовлетворяют условиям:
(1)
(2)
Элементы матрицы pij – дают вероятности переходов в системе за один шаг. Переход
Si – Sj за два шага можно рассматривать как происходящий на первом шаге из Si в некоторое промежуточное состояние Sk и на втором шаге из Sk в Si. Таким образом, для элементов матрицы вероятностей переходов из Si в Sj за два шага получим:
|
|
|
В общем случае перехода 
за m шагов для элементов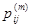 
матрицы вероятностей переходов справедлива формула:
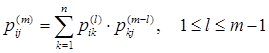(3)
Получим два эквивалентных выражения для :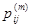
Пусть система S описывается матрицей вероятностей переходов Р:
Если обозначить через Р(m) матрицу, элементами которой являются рi вероятности переходов из Si в Sj за m шагов, то справедлива формула
,
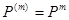где матрица Рm получается умножением матрицы P саму на себя m раз.
Исходное состояние системы характеризуется вектором состояния системы Q(qi) (называемым также стохастическим вектором).
где qj - вероятность того, что исходным состоянием системы является Sj состояние. Аналогично (1) и (2) справедливы соотношения
Обозначим через
вектор состояния системы после m шагов, где qj – вероятность того, что после m шагов система находится в Si состоянии. Тогда справедлива формула
Если вероятности переходов Pij остаются постоянными, то такие марковские цепи называются стационарными. В противном случае марковская цепь называется нестационарной.
|
|
|
