Процессы рождения и гибели

 

Так называется широкий класс случайных процессов, происходящих в системе, размеченный граф состояний которой изображен на рис. 3.

 

Рисунок 2 – Граф состояний для процессов гибели и размножения

 

Здесь величины , ,…,  – интенсивности переходов системы из состояния в состояние слева направо, можно интерпретировать как интенсивности рождения (возникновения заявок) в системе. Аналогично, величины , ,…,  – интенсивности переходов системы из состояния в состояние справа налево, можно интерпретировать как интенсивности гибели (выполнения заявок) в системе.

Поскольку все состояния являются сообщающимися и существенными, существует (в силу теоремы 2) предельное (финальное) распределение вероятностей состояний. Получим формулы для финальных вероятностей состояний системы.

В стационарных условиях для каждого состояния поток, входящий в данное состояние должен равняться потоку, исходящему из данного состояния. Таким образом, имеем:

Для состояния S₀:

 

 

Следовательно:

Для состояния S₁:

 

 

Следовательно:

 

 

С учетом того, что :

 

 

Аналогично получаем уравнения для остальных состояний системы. В результате получим систему уравнений:

 

 

Решение этой системы будет иметь вид:

 

                                     (4)

, ,…,                                   (5)

Основные понятия и классификация систем массового обслуживания

 

Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение заявки называется обслуживанием заявки.

Системой массового обслуживания (СМО) называется любая система для выполнения заявок, поступающих в неё в случайные моменты времени.

Поступление заявки в СМО называется событием. Последовательность событий, заключающихся в поступлении заявок в СМО, называется входящим потоком заявок. Последовательность событий, заключающихся в выполнении заявок в СМО, называется выходящим потоком заявок.

Поток заявок называется простейшим, если он удовлетворяет следующим условиям:

1) отсутствие последействия, т.е. заявки поступают независимо друг от друга;

2) стационарность, т.е. вероятность поступления данного числа заявок на любом временном отрезке [t₁; t₂] зависит лишь от величины этого отрезка и не зависит от значения t₁, что позволяет говорить о среднем числе заявок за единицу времени, λ, называемом интенсивностью потока заявок;

3) ординарность, т.е. в любой момент времени в СМО поступает лишь одна заявка, а поступление одновременно двух и более заявок пренебрежимо мало.

Для простейшего потока вероятность p_i(t) поступления в СМО ровно i заявок за время t вычисляется по формуле:

 

                                                             (6)

т.е. вероятности распределены по закону Пуассона с параметром λt. По этой причине простейший поток называется также пуассоновским потоком.

Функция распределения F(t) случайного интервала времени T между двумя последовательными заявками по определению равна . Но , где  – вероятность того, что следующая после последней заявки поступит в СМО по истечении времени t, т.е. за время t в СМО не поступит ни одна заявка. Но вероятность этого события находится из (6) при i = 0. Таким образом:

 

                                  

                                                                            (7)

 

Плотность вероятности f(t) случайной величины T определяется формулой:

 

   ,

 

Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины T равны соответственно:

 

 

Каналом обслуживания называется устройство в СМО, обслуживающее заявку. СМО, содержащее один канал обслуживания, называется одноканальной, а содержащее более одного канала обслуживания – многоканальной.

Если заявка, поступающая в СМО, может получить отказ в обслуживании (в силу занятости всех каналов обслуживания) и в случае отказа вынуждена покинуть СМО, то такая СМО называется СМО с отказами.

Если в случае отказа в обслуживании заявки могут вставать в очередь, то такие СМО называются СМО с очередью (или с ожиданием). При этом различают СМО с ограниченной и неограниченной очередью. Очередь может быть ограничена как по количеству мест, так и по времени ожидания. Различают СМО открытого и замкнутого типа. В СМО открытого типа поток заявок не зависит от СМО. В СМО замкнутого типа обслуживается ограниченный круг клиентов, а число заявок может существенно зависеть от состояния СМО (например, бригада слесарей – наладчиков, обслуживающих станки на заводе).

СМО могут также различаться по дисциплине обслуживания.

Если в СМО нет приоритета, то заявки отбираются из очереди в канал по различным правилам.

· Первым пришел – первым обслужен (FCFS – First Came – First Served)

· Последним пришел – первым обслужен (LCFS – Last Came – First Served)

· Первоочередное обслуживание требований с кратчайшей длительностью обслуживания (SPT/SJE)

· Первоочередное обслуживание требований с кратчайшей длительностью дообслуживания (SRPT)

· Первоочередное обслуживание требований с кратчайшей средней длительностью обслуживания (SEPT)

· Первоочередное обслуживание требований с кратчайшей средней длительностью дообслуживания (SERPT)

Приоритеты бывают двух типов – абсолютный и относительный.

Если требование в процессе обслуживания может быть удалено из канала и возвращено в очередь (либо вовсе покидает СМО) при поступлении требования с более высоким приоритетом, то система работает с абсолютным приоритетом. Если обслуживание любого требования, находящегося в канале не может быть прервано, то СМО работает с относительным приоритетом. Существуют также приоритеты, осуществляемые с помощью конкретного правила или набора правил. Примером может служить приоритет, изменяющийся с течением времени.

СМО описываются некоторыми параметрами, которые характеризуют эффективность работы системы.

 – число каналов в СМО;

 – интенсивность поступления в СМО заявок;

 – интенсивность обслуживания заявок;

 

 – коэффициент загрузки СМО;

 

 – число мест в очереди;

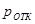 – вероятность отказа в обслуживании поступившей в СМО заявки;

 – вероятность обслуживания поступившей в СМО заявки (относительная пропускная способность СМО);

При этом:

 

                                                              (8)

 

А – среднее число заявок, обслуживаемых в СМО в единицу времени (абсолютная пропускная способность СМО)

 

                                                                            (9)

 

 – среднее число заявок, находящихся в СМО

 – среднее число каналов в СМО, занятых обслуживанием заявок. В тоже время это 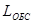 – среднее число заявок, обслуживаемых в СМО за единицу времени. Величина  определяется как математическое ожидание случайного числа занятых обслуживанием n каналов.

 

,                                                 (10)

 

где  – вероятность нахождения системы в S_k состоянии.

 – коэффициент занятости каналов

 – среднее время ожидания заявки в очереди

 – интенсивность ухода заявок из очереди

 – среднее число заявок в очереди. Определяется как математическое ожидание случайной величины m – числа заявок, состоящих в очереди

 

                                                              (11)

 

Здесь  – вероятность нахождения в очереди i заявок;

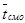 – среднее время пребывания заявки с СМО

 – среднее время пребывания заявки в очереди

Для открытых СМО справедливы соотношения:

 

                                                                  (12)

                                                                             (13)

Эти соотношения называются формулами Литтла и применяются только для стационарных потоков заявок и обслуживания.

Рассмотрим некоторые конкретные типы СМО. При этом будет предполагаться, что плотность распределения промежутка времени между двумя последовательными событиями в СМО имеет показательное распределение (7), а все потоки являются простейшими.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: