 |
Случайная величина с экспоненциальным распределением
|
|
|
|
Простейшим потоком (или потоком Пуассона) называется такой поток заявок, когда промежуток времени 
между двумя последовательными заявками есть случайная величина, распределенная на интервале 
с плотностью
Вычислим математическое ожидание: 
После интегрирования по частям, получим:
.
Параметр 
есть интенсивность потока заявок.
Формулу для розыгрыша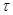 
получим из уравнения (30), которое в данном случае запишется так: 
.
Вычислив интеграл, стоящий слева, получим соотношение 
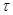. Отсюда, выражая , получим:
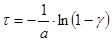(33)
Т.к. величина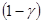 
распределена также как и 
, следовательно, формулу (33) можно записать в виде:
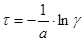(34)
Исследование системы массового обслуживания
Проверка гипотезы о показательном распределении
Исследуемое мной предприятие представляет собой двухканальную систему массового обслуживания с ограниченной очередью. На вход поступает пуассоновский поток заявок с интенсивностью λ. Интенсивности обслуживания заявок каждым из каналов μ, а максимальное число мест в очереди m.
Начальные параметры:
Время обслуживания заявок имеет эмпирическое распределение, указанное ниже и имеет среднее значение 
.
Мной были проведены контрольные замеры времени обработки заявок, поступающих в данную СМО. Чтобы приступить к исследованию, необходимо установить по этим замерам закон распределения времени обработки заявок.
Таблица 6.1 – Группировка заявок по времени обработки
| Количество заявок | 22 | 25 | 23 | 16 | 14 | 10 | 8 | 4 |
| Время обработки, мин | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 | 30–35 | 35–40 |
|
|
|
Выдвигается гипотеза о показательном распределении генеральной совокупности.
Для того чтобы, при уровне значимости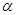 
проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
1) Найти по заданному эмпирическому распределению выборочную среднюю 
. Для этого, каждый i – й интервал заменяем его серединой 
и составляем последовательность равноотстоящих вариант и соответствующих им частот.
2) Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней:
3) Найти вероятности попадания X в частичные интервалы по формуле:
4) Вычислить теоретические частоты:
,
где 
- объем выборки
5) Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы 
, где S – число интервалов первоначальной выборки.
Таблица 6.2 – Группировка заявок по времени обработки с усредненным временным интервалом
| Количество заявок | 22 | 25 | 23 | 16 | 14 | 10 | 8 | 4 |
| Время обработки, мин | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | 37,5 |
Найдем выборочную среднюю:
2) Примем в качестве оценки параметра λ экспоненциального распределения величину, равную 
. Тогда:
(
)
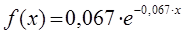3) Найдем вероятности попадания X в каждый из интервалов по формуле:
Для первого интервала:
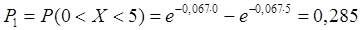
Для второго интервала:
Для третьего интервала:
Для четвертого интервала:
Для пятого интервала:
Для шестого интервала:
Для седьмого интервала:
Для восьмого интервала:
4) Вычислим теоретические частоты:
Результаты вычислений заносим в таблицу. Сравниваем эмпирические 
и теоретические 
частоты с помощью критерия Пирсона.
|
|
|
Для этого вычислим разности 
, их квадраты, затем отношения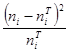 
. Суммируя значения последнего столбца, находим наблюдаемое значение критерия Пирсона. По таблице критических точек распределения 
при уровне значимости 
и числу степеней свободы 
находим критическую точку 
Таблица 6.3 – Результаты вычислений
| i | 
| 
| 
| 
| 
|
|
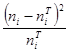
| 1 | 22 | 0,285 | 34,77 | -12,77 | 163,073 | 4,690 |
| 2 | 25 | 0,204 | 24,888 | 0,112 | 0,013 | 0,001 |
| 3 | 23 | 0,146 | 17,812 | 5,188 | 26,915 | 1,511 |
| 4 | 16 | 0,104 | 12,688 | 3,312 | 10,969 | 0,865 |
| 5 | 14 | 0,075 | 9,15 | 4,85 | 23,523 | 2,571 |
| 6 | 10 | 0,053 | 6,466 | 3,534 | 12,489 | 1,932 |
| 7 | 8 | 0,038 | 4,636 | 3,364 | 11,316 | 2,441 |
| 8 | 4 | 0,027 | 3,294 | 0,706 | 0,498 | 0,151 |
| 122 | 
|
Т.к. 
, то нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой.
|
|
|
