 |
Выпрямление граничных линий.
|
|
|
|
В хозяйственном отношении выгодно, если общие граничные линии проходят по возможности прямолинейно. Если на местности граница между двумя земельными участками ломаная, то оба владельца этих участков могут согласиться на новую прямолинейную границу, которая, однако, не меняет величины площадей. Проведение новой граничной линии должно привести к выравниванию площадей. При этом в общем случае можно исходить их факта, что земля по обе стороны границы равноценна. Если это условие не соблюдается, то вместо выравнивания площадей необходимо стремиться к выравниванию ценности участков. Если выпрямляются границы участков частной собственности, то все измерения должны проводиться официально уполномоченными лицами.
Как и в случае деления площадей, задача решается строго только в тех случаях, если она может быть приведена к решению простых задач. В трудных случаях быстрее всего выполняется графическое решение методом последовательных приближений.
8.1. Выпрямление граничной линии параллельно базисной линии.
Направление базисной линии, относительно которой измеряется на местности ломаный ход граничных линий, может быть выбрано свободно. Она может проходить и перпендикулярно к существующей границе. Базисная линия переносится на местность в желаемом направлении таким образом, чтобы по возможности имело место равенство площадей. После этого измеряются все граничные пункты по методу прямоугольных координат относительно базисной линии. Новая линия раздела должна проходить параллельно перенесенной базисной линии так, чтобы площади были равны. Вычисление элементов разбивки новой линии раздела выполняется аналогично предыдущей задаче. Определяется разность площадей, находящихся по обе стороны базисной линии, которая перемещается параллельно до тех пор, пока образующаяся полоса не будет равна разности площадей.
|
|
|
Решение методом приближений. Пусть базисная линия направлена параллельно границе АН (рис. 21). Однако выпрямленная граница должна проходить параллельно линии АJ. Разность площадей остается – 493 м2. Если площади выше базисной линии, то они считаются положительными, а если ниже – отрицательными. Базисную линию необходимо перемещать вниз на величину у в положение МК, чтобы площадь АJКМ равнялась ΔF, т. е. 493 м2. Фигура АJКМ есть трапеция, которую сначала приближенно можно рассматривать как прямоугольник. Длина у=АМ приближенно равна
у≈  м.
м.

Рис. 21. Выпрямление границы параллельно базисной линии
Если бы границы НА и FG были взаимно параллельными, то 5,15 м представляло бы уже окончательную величину перемещения. Но в этом случае площадь меньше на величину треугольника GKL. Для вычисления площади треугольника необходимо иметь еще отрезок LJ. Он равен
LJ= 
Следовательно, площадь треугольника JKL равна
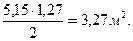
Линию раздела необходимо перемещать вниз еще на величину

Согласно этому предварительное расстояние новой границы от осевой линии равно 5,18 м. Контрольное вычисление для ΔF должно было давать нуль. Практически получено
ΔF=-1,19 м2.
Из этого можно получить второе перемещение

Окончательное значение для у, следовательно, равно
у=5,19 м.
Повторное вычисление дает
ΔF=-0,1 м2,
и поэтому дальнейшего перемещения линии раздела не требуется.
Для перенесения на местность целесообразно вычислить отрезки LJ и JK. Имеем:
LJ= 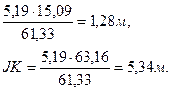
Длина х линии раздела МК оказалась равной 94,39 м. На рисунке 21 показаны все измеренные и вычисленные данные.
8.2. Строгое решение.
В этом методе вычисляется разность площадей ΔF, расположенных по обе стороны базисной линии. Эту разность можно понимать и как разность площадей двух треугольников АJS и МКS, если представить себе, что прямолинейные граничные линии АН и FG пересекаются в точке S. Если обозначить угол JАН через α, угол АJG через β и длину новой границы через х, то имеем
|
|
|


или относительно х

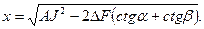
Расстояние у между базисной линией АJ и параллельно ей проходящей новой границей МК вычисляется из уравнения 
Для числового примера получаем  так как α=100º и
так как α=100º и


Рис. 23. Выпрямление русла реки
|
|
|


