Три задачи по расчету простого трубопровода

Все основные расчеты, связанные с простым трубопроводом сводятся к решению следующих трех задач.

Задача 1. Заданы: Напор H, диаметр d и длина l трубопровода, все величины z_i, к_э и n.

Определить: Расход Q.

Ошибочной в данном случае может показаться простота решения уравнения (1.7) путем извлечения квадратного корня. На самом деле во всех зонах, кроме квадратичной, величина l зависит от числа Rе

,

а, следовательно, от расхода Q. Если подойти формально к решению второй задачи, то (1.7) представляет уравнение с одним неизвестным, которое решается по известным алгоритмам с помощью ЭВМ. В инженерной практике может быть полезен прием решения (1.7) называемый графоаналитическим способом. Если задаться несколькими (5 - 10) произвольными, но реальными числовыми значениями расхода Q и подставить их в (1.7), то получится столько же числовых значений Н. Затем в системе координат Q – H наносят эти точки и соединяют их плавной кривой; она, как видно из (1.7) представляет квадратичную параболу, симметричную относительно оси H, рис. 1.2., (имеет смысл ее ветвь при Q > 0).

Построенная по точкам, она отражает зависимость Q от H только для данного трубопровода, поэтому из графика по известному значению Н находят искомое значение Q.

Рис. 1.2. Рис. 1.3.

Необходимо задавать такие величины расходов, чтобы получать напоры как меньшие, так и большие заданного.

Задача 1.1 Определить величину расхода Q, проходящему по трубопроводу диаметром d=50мм и длиной l=115м, если разность уровней в начале и в конце трубопровода равна Н=4,3м. Трубы стальные, К_Э=0,05мм, сумма всех коэффициентов местных сопротивлений равна 3,2, т.е. Σξ=3,2.

Решение. В данном случае имеем одно уравнение (1,7) и одну неизвестную величину – расход Q, поэтому задачу лучше всего решать на ЭВМ одним из известных приближенных методов. Для инженерных расчетов применим простейший метод подбора. В качестве первоначального задаем расход, равный Q₁=2,5л/с. Посмотрим теперь, какому значению напора Н соответствует заданное значение Q₁=2,5л/с, т. е. решаем первую задачу по расчету простого трубопровода. Находим последовательно: Re₁=63694, (Re₁·К_Э)/d=64, λ₁=0,023, Н₁=4,8м. Получен напор, больший заданного, поэтому необходимо взять меньший расход, например Q₂=2,2л/с, при этом расходе: Re₂=56051, (Re₂·К_Э)/d=56, λ₂=0,024, Н₂=3,8м. Ясно, что искомый расход заключен между Q₁ и Q₂ и любой расход, взятый из этого промежутка сужает интервал поиска. Продолжая задание расходов из интервала Q₁ > Q_X > Q₂ и сравнивая полученные значения Н_Х с заданным Н=4,3м, возможно решить задачу с любой точностью.

Если в данном случае применить формулу

,

то получим (определяя λ как в квадратичной зоне) Q=2,57л/с, что является завышенным по сравнению с действительным значением.

Задача 2. Заданы: Напор Н, расход Q, длина трубопровода, все величины z_i, к_э и n.

Определить: Диаметр d.

В этом случае уравнение (1.7) невозможно решить аналитически, но формально – это уравнение с одним неизвестным и решение его на ЭВМ трудностей не представляет. Для инженерных расчетов удобно применить графо-аналитический способ. Кривая зависимости H от d является гиперболой; как это следует из (1.7): при d → 0, H → ∞. При d → ∞, H → 0, рис. 1.3.

Для решения задач задают несколько значений диаметров, строят кривую и по известному значению Н находят искомое значение d.

Задача 1.2. Определить диаметр трубопровода, который должен пропускать расход Q=5,6л/с при действующем напоре Н=3,0м. Длина трубопровода l=80м, К_Э=0,05мм, сумма коэффициентов местных сопротивлений на трубопроводе Σξ=4,5.

Решение второй и третьей задач по расчету простого трубопровода продолжается до тех пор, пока не выполнится равенство

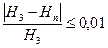
где 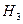-заданное значение напора; -полученное в результате решения значение напора.

Вторая задача.

№ варианта	H см	l м	К, мм	∑ƺ	d мм	ν
	640,754		0,02	0,900		0,010
	127,469		0,05	2,400		0,010
	624,507		0,07	3,200		0,010
	28,708		0,08	5,000		0,010
	1036,719		0,03	1,100		0,010
	118,823		0,05	2,300		0,010
	32,681		0,04	4,300		0,010
	2028,987		0,02	2,000		0,010
	321,656		0,06	1,700		0,010
	167,787		0,01	2,700		0,010
	49,601		0,02	3,300		0,010
	24,164		0,08	4,700		0,010
	268,806		0,01	5,000		0,010
	1344,967		0,07	1,600		0,010
	80,297		0,03	2,400		0,010
	68,651		0,02	3,700		0,010
	577,633		0,08	4,200		0,010
	180,961		0,02	0,900		0,010
	57,359		0,07	0,800		0,010
	6734,137		0,03	1,100		0,010
	791,771		0,04	2,300		0,010
	80,799		0,08	1,300		0,010
	16,715		0,03	5,000		0,010
	1091,942		0,06	2,800		0,010
	2380,693		0,06	4,900		0,010
	221,021		0,08	5,300		0,010
	32,582		0,02	2,600		0,010
	38,43		0,03	0,800		0,010
	1359,109		0,07	1,700		0,010
	18,22		0,06	3,500		0,010
	29,034		0,04	4,700		0,010
	26,398		0,05	3,800		0,010
	38,053		0,02	2,900		0,010
	149,095		0,08	4,300		0,010
	574,918		0,07	3,700		0,010
	127,313		0,03	2,600		0,010
	115,492		0,01	1,900		0,010
	25,573		0,02	0,900		0,010
	38,195		0,01	0,800		0,010
	3320,013		0,01	2,300		0,010
	4,366		0,04	5,000		0,010
	7,977		0,01	3,400		0,010
	3168,72		0,05	2,900		0,010
	670,417		0,02	3,300		0,010
	91,39		0,04	4,200		0,010
	4,686		0,01	2,100		0,010
	16,073		0,08	3,100		0,010
	1968,884		0,02	0,900		0,010
	1657,434		0,01	0,800		0,010
	117,802		0,06	0,800		0,010
	180,928		0,07	0,900		0,010
	124,688		0,02	1,200		0,010
	86,698		0,01	0,900		0,010
	106,186		0,03	2,300		0,010
	217,507		0,01	4,600		0,010
	67,721		0,05	4,700		0,010
	713,265		0,04	4,800		0,010
	4359,757		0,06	3,900		0,010
	253,372		0,07	2,900		0,010
	153,16		0,08	0,900		0,010
	5,023		0,01	2,800		0,010
	2,629		0,02	2,400		0,010
	3083,899		0,03	2,700		0,010
	45,533		0,02	3,700		0,010
	514,298		0,01	0,900		0,010
	76,496		0,08	0,800		0,010
	12,275		0,06	0,900		0,010
	4837,246		0,07	3,200		0,010
	39,852		0,04	3,300		0,010
	17,754		0,03	3,800		0,010
	6915,872		0,02	5,000		0,010
	22,297		0,01	3,700		0,010
	25,982		0,02	2,500		0,010
	49,841		0,06	2,200		0,010
	144,446		0,04	3,300		0,010
	35,334		0,01	0,900		0,010
	2773,964		0,08	0,800		0,010
	325,289		0,05	1,200		0,010
	17882,166		0,06	2,600		0,010
	90,806		0,07	2,800		0,010
	14,802		0,03	3,400		0,010
	187,901		0,05	3,600		0,010
	22,842		0,01	4,600		0,010
	18,328		0,02	4,100		0,010
	22,392		0,08	3,100		0,010
	92,043		0,07	2,900		0,010
	1466,167		0,02	0,900		0,010
	795,597		0,01	0,800		0,010
	89,642		0,02	2,400		0,010
	49,545		0,03	2,900		0,010
	32,331		0,04	5,000		0,010
	4358,041		0,05	4,300		0,010
	14,81		0,06	5,000		0,010
	23,942		0,07	4,700		0,010
	50,651		0,02	5,000		0,010
	87,862		0,08	4,800		0,010
	75,343		0,02	5,000		0,010
	63,841		0,01	4,900		0,010
	207,777		0,02	0,900		0,010
	14276,663		0,06	0,800		0,010
	81,565		0,05	5,000		0,010

Третья задача.

№ варианта	H, см	Q л/с	l м	K, мм	∑ƺ	ν
	791,771	1,14		0,04	2,3	0,010
	80,799	1,29		0,08	1,3	0,010
	16,715	1,33		0,03		0,010
	1091,942	1,42		0,06	2,8	0,010
	2380,693	1,56		0,06	4,9	0,010
	221,021	1,67		0,08	5,3	0,010
	32,582	1,71		0,02	2,6	0,010
	38,43	1,88		0,03	0,8	0,010
	1359,109	1,91		0,07	1,7	0,010
	18,22	2,03		0,06	3,5	0,010
	29,034	2,17		0,04	4,7	0,010
	26,398	2,23		0,05	3,8	0,010
	38,053	2,34		0,02	2,9	0,010
	149,095	2,46		0,08	4,3	0,010
	574,918	2,57		0,07	3,7	0,010
	127,313	2,68		0,03	2,6	0,010
	115,492	2,71		0,01	1,9	0,010
	25,573	2,83		0,02	0,9	0,010
	38,195	2,92		0,01	0,8	0,010
	3320,013			0,01	2,3	0,010
	4,366	1,19		0,04		0,010
	127,469	1,35		0,05	2,4	0,010
	624,507	1,21		0,07	3,2	0,010
	28,708			0,08		0,010
	1036,719	1,51		0,03	1,1	0,010
	118,823	1,77		0,05	2,3	0,010
	32,681	1,63		0,04	4,3	0,010
	2028,987	1,82		0,02		0,010
	321,656	1,94		0,06	1,7	0,010
	167,787	2,05		0,01	2,7	0,010
	49,601	2,14		0,02	3,3	0,010
	24,164	2,23		0,08	4,7	0,010
	268,806	2,38		0,01		0,010
	1344,967	2,45		0,07	1,6	0,010
	80,297	2,54		0,03	2,4	0,010
	68,651	2,67		0,02	3,7	0,010
	577,633	2,79		0,08	4,2	0,010
	180,961	2,85		0,02	0,9	0,010
	57,359	2,93		0,07	0,8	0,010
	6734,137			0,03	1,1	0,010
	17,754	2,09		0,03	3,8	0,010
	7,977	1,24		0,01	3,4	0,010
	3168,72	1,35		0,05	2,9	0,010
	670,417	1,47		0,02	3,3	0,010
	91,39	1,59		0,04	4,2	0,010
	4,686	1,66		0,01	2,1	0,010
	16,073	1,77		0,08	3,1	0,010
	1968,884	1,83		0,02	0,9	0,010
	1657,434	1,97		0,01	0,8	0,010
	117,802	2,01		0,06	0,8	0,010
	180,928	2,12		0,07	0,9	0,010
	124,688	2,23		0,02	1,2	0,010
	86,698	2,34		0,01	0,9	0,010
	106,186	2,46		0,03	2,3	0,010
	14,802	1,15		0,03	3,4	0,010
	187,901	1,29		0,05	3,6	0,010
	22,842	1,34		0,01	4,6	0,010
	18,328	1,49		0,02	4,1	0,010
	22,392	1,57		0,08	3,1	0,010
	92,043	1,65		0,07	2,9	0,010
	217,507	2,58		0,01	4,6	0,010
	67,721	2,61		0,05	4,7	0,010
	1466,167	1,71		0,02	0,9	0,010
	795,597	1,81		0,01	0,8	0,010
	89,642	1,92		0,02	2,4	0,010
	49,545	2,05		0,03	2,9	0,010
	32,331	2,16		0,04		0,010
	4358,041	2,23		0,05	4,3	0,010
	39,852	1,93		0,04	3,3	0,010
	53,933	1,67		0,06	3,6	0,010
	6915,872	2,12		0,02		0,010
	22,297	2,26		0,01	3,7	0,010
	25,982	2,37		0,02	2,5	0,010
	49,841	2,44		0,06	2,2	0,010
	144,446	2,55		0,04	3,3	0,010
	35,334	2,67		0,01	0,9	0,010
	2773,964	2,76		0,08	0,8	0,010
	325,289	2,83		0,05	1,2	0,010
	17882,166	2,96		0,06	2,6	0,010
	90,806			0,07	2,8	0,010
	14,81	2,39		0,06		0,010
	23,942	2,48		0,07	4,7	0,010
	50,651	2,55		0,02		0,010
	87,862	2,63		0,08	4,8	0,010
	75,343	2,76		0,02		0,010
	63,841	2,83		0,01	4,9	0,010
	207,777	2,99		0,02	0,9	0,010
	14276,663			0,06	0,8	0,010
	81,565	1,19		0,05		0,010
	4359,757	2,83		0,06	3,9	0,010
	253,372	2,96		0,07	2,9	0,010
	153,16			0,08	0,9	0,010
	5,023	1,15		0,01	2,8	0,010
	2,629	1,26		0,02	2,4	0,010
	3083,899	1,39		0,03	2,7	0,010
	45,533	1,46		0,02	3,7	0,010
	514,298	1,57		0,01	0,9	0,010
	76,496	1,69		0,08	0,8	0,010
	12,275	1,73		0,06	0,9	0,010
	4837,246	1,81		0,07	3,2	0,010

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: