Последовательное соединение

Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным, рис. 3.1. А В

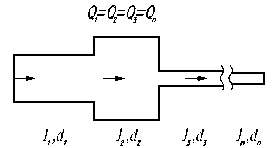
Рис.3.1. Рис.3.2.

 

(3.1)

Очевидно, что расход во всех последовательно соединенных трубах один и тот же, а полные потери напора Н для всего трубопровода равны сумме потерь напора на всех участках, т.е.

(3.2)

Q₁ = Q₂ = Q₃ = …= Q_n = Q

H = H₁ + H₂ + H₃ + …+ H_n,

где H₁, H₂ , H₃, …, H_n – потери напора на 1, 2, 3, …n-ом участке.

Учитывая, что для каждого участка последовательного соединения справедлива зависимость (1.7) и имея в виду, что на каждом участке расход одинаковый, запишем (3.2) в виде:

(3.3)

.

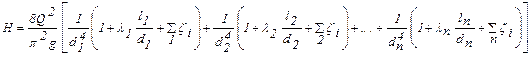Из (4.3) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же как для простого трубопровода (трубопровода постоянного диаметра).

Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (3.3) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.

Задача 3.1. Определить потери напора в стальном трубопроводе, состоящем из двух участков длиной l ₁ = 120 м и l ₂ = 250 м. Диаметры труб участков d ₁ = 120 мм и d ₂ = 100 мм. Расход воды в трубопроводе Q = 12,2 л/с, кинематический коэффициент вязкости воды принять равным n = 0,01 см²/с.

Решение. В данном случае общие потери равны сумме потерь на каждом из участков. По справочнику определяем к_Э = 0,02 мм.

Определяем последовательно для первого участка

V₁ = 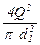= 1,1 м/с; Re₁ = 129511; Re₁× = 10,7; l₁ = 0,017;

Аналогично для второго участка

V₂ = 1,55 м/с; Re₂ = 155414; Re₂ = 31; l₂ = 0,017;

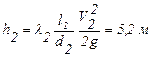; h₁ + h ₂ = 6.23 м.

Ответ: общие потери напора равны 6,23 м.

Параллельное соединение

При параллельном соединении участков трубопровода жидкость, подходя с общим расходом Q к точке их разветвления А, распределяется по параллельным участкам (ветвям, ответвлениям) и далее снова собирается в точке их соединения В, рис. 3.2.

При параллельном соединение обычно задается

1.Суммарный расход до точки разветвления,

2. Основные данные для каждой ветви, т.е. длина, диаметр, абсолютная широховатость поверхности стенки, коэффициенты местных сопротивлений , которые есть на ветви.

Основными задачами гидравлического расчета параллельного соединения являются:

1.Определение расходов Q₁, Q₂, Q₃, …, Q_n, на отдельных участках, соединенным параллельно.

2.Определение потерь напора Δh между точками А и В, на каждом участке.

При решении задачи используется очевидное условие: суммарный (общий) расход Q равен сумме всех расходов во всех ветвях, т.е.

(3.4)

Q = Q₁ + Q₂ + Q₃ +…+ Qn,

Для дальнейшего решения задачи представим, что в точках А и В установлены пьезометры (трубки, в которых жидкость поднимается на высоту, пропорциональную давлению в точке присоединения); так как концы всех трубопроводов соединяются в одних и тех же точках А и В, то потери на всех этих участках (ветвях) параллельного соединения одинаковы и равны Δh (Δh – разность показаний пьезометров установленных в точках А и В). Поэтому справедливо следующие равенство

(3.5)

Δh = Δh ₁ = Δh ₂ = Δh ₃ = …= Δh _n

Система уравнений (3.4) и (3.5) является исходной при решении задачи о параллельном соединении.

На практике для расчета параллельного соединения часто используют метод характеристик; изложим его для дальнейшего применения при решении задачи 3.1 (число ветвей равно трем). При применении этого метода коэффициенты сопротивления трения параллельных ветвей не задается. Известными величинами являются: общий расход Q, диаметры труб ветвей , длина трубы каждой ветви 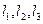, величины абсолютной шероховатости к (они определяются по таблицам исходя из материала труб). Решение задачи производится графическим способом, поэтому желательно для повышения точности результатов применять миллиметровую бумагу.

Для решения задачи в данном случае на графике Δh – Q производится построение характеристик всех трех ветвей, рис.3.3. Напомним, что для построения характеристик любой из трех ветвей назначается произвольно от 4 до 8 расходов и по назначенному произвольным образом расходу находится значение потерь Δh по формуле:

,

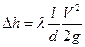где l- длина ветви; d - диаметр трубы ветви; V=Q/S, S - площадь сечения трубы; Q- назначенный расход.

Таким образом, на одном графике строятся все три характеристики.

Далее, при некотором произвольном значении Δh 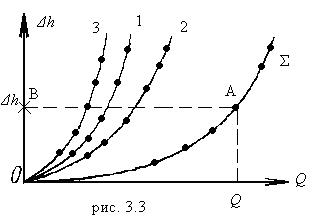проводится горизонтальная прямая и вдоль нее суммируются расходы всех трех характеристик; в результате на графике появится точка 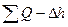. Таких точек (при различных значениях Δh) необходимо найти 5-6 и по ним построить результирующую кривую. Она по своему смыслу выражает зависимость потерь Δh от суммарного (общего) расхода Q. Но общий расход Q задан, поэтому откладывается его значение на горизонтальной оси Q, проводят перпендикуляр до пересечения с суммарной кривой и в точке пересечения находят соответствующие значение Δh (расходы в ветвях находят по точкам пересечения горизонтальной прямой А-В с характеристиками ветвей).

 

Задача 3.2. В водопроводной сети есть участок А-В с тремя параллельными ветвями (рис. 3.4). Определить потерю напора на каждой ветви (на участке А-В) и расходы в ветвях Q_1, Q_2, Q_3, если общий расход в магистрали равен Q. Диаметры d и длины участков l заданы. Трубы стальные новые. Задачу решить методом характеристик. Принять кинематический коэффициент вязкости равным . Рекомендуется все длины выражать в см; при этом .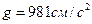

 

 

Рис. 3.4

 

№ варианта	Q, л/с	Диаметр трубы, d мм	Длины участков, l, м

 

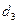
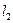
⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: