 |
Методические указания к выполнению контрольной работы №1
|
|
|
|
В рекомендованных учебниках [1], [2], а также в руководствах [4J и [5] учащиеся найдут достаточное число примеров задач подобных тем, которые включены в контрольную работу. Поэтому ниже даны лишь необходимые краткие методические указания к решению задач контрольной работы.
Первую задачу (задачи 1 —10) следует решить после изучения тем 1.1.1 и 1.1.2.1. Во всех задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Можно избрать три способа решения: аналитический, графический и геометрический. Для данного типа задач целесообразно использовать аналитический способ решения.
Последовательность решения задачи:
1 Выбрать тело (точку), равновесие которого следует рассматривать.
2 Освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принято предполагать, что стержни растянуты.
3 Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ∑ Xi = 0; ∑Уi =0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.
4 Определить реакции стержней из решения указанной системы уравнений.
Пример 1 Определить реакции стержней, удерживающих грузы F1 = 70 кН и F2 = 100 кН (рис. 1,а). Массой стержней пренебречь.
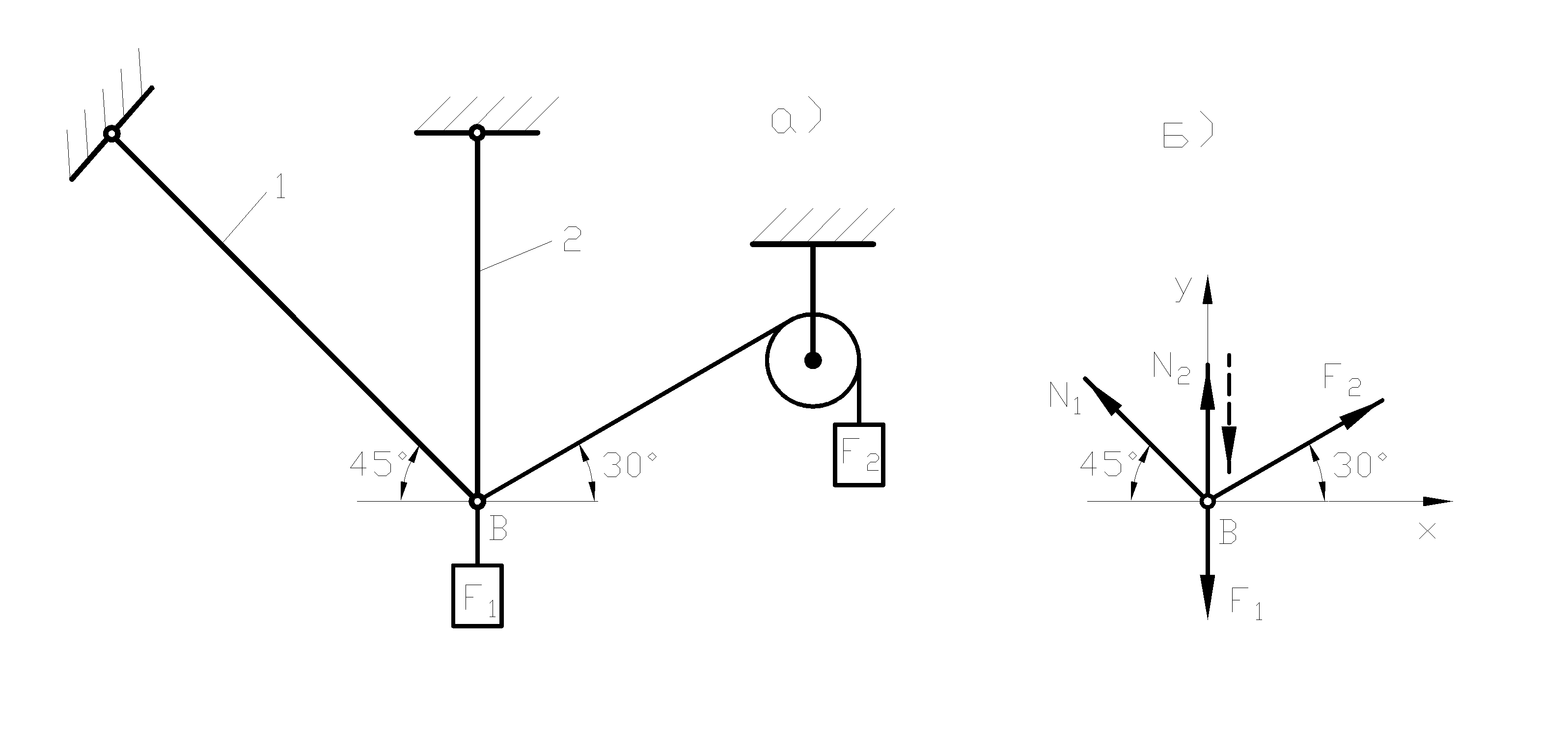
Рисунок 1
Решение: 1 Рассматриваем равновесие шарнира В(рисунок 1, а).
|
|
|
2 Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рисунок 1, б ).
3 Выбираем систему координат, совместив ось упо направлению с реакцией N2 (рисунок 1, б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:
∑Xi = -N1·cos 45° + F2· cos 30° = 0 (1)
∑Yi = N1·sin45° + N2 + F2·sin30° - F1 = 0 (2)
4 Определяем реакции стержней N1 и N2, решая уравнения (1), (2).
Из уравнения (1)
N1 = F2 · cos 30° / cos 45° = 100 · 0,866/0,707 = 122 кН
Подставляя найденное значение N1 в уравнение (2), получаем
N2 = F1 - F2 · sin 30° - N1 · sin 45° = 70 - 100 · 0,5 - 122 · 0,707 = -66,6 кН
Знак минус перед значением N2 указывает на то, что первоначально выбранное направление реакции неверное - следует направить реакцию N2 в противоположную сторону, т. е. к шарниру В (на рисунке 1,б истинное направление реакции N2 показано штриховым вектором).
Задачи 1 — 10 Определить реакции стержней, удерживающих грузы F1и F2.Массой стержней пренебречь. Схему своего варианта смотри на рисунке 2. Числовые данные своего варианта взять из таблицы 2.
Таблица 2
| № задачи и схемы на рис. 2 | F1 | F2 | |||||||||
| 2 | 3 | 9 | 10 | ||||||||||
| Варианты | кН | ||||||||||
| 0,4 | 0,5 | ||||||||||
| 0,3 | 0,8 | ||||||||||
| 0,6 | 0,4 | ||||||||||
| 0,2 | 0,5 | ||||||||||
| 0,5 | 0,8 | ||||||||||
| 0,8 | 0,4 | ||||||||||
| 0,4 | 0,2 | ||||||||||
| 1,2 | 0,8 | ||||||||||
| 0,8 | 1,0 | ||||||||||
| 0,9 | 0,6 |
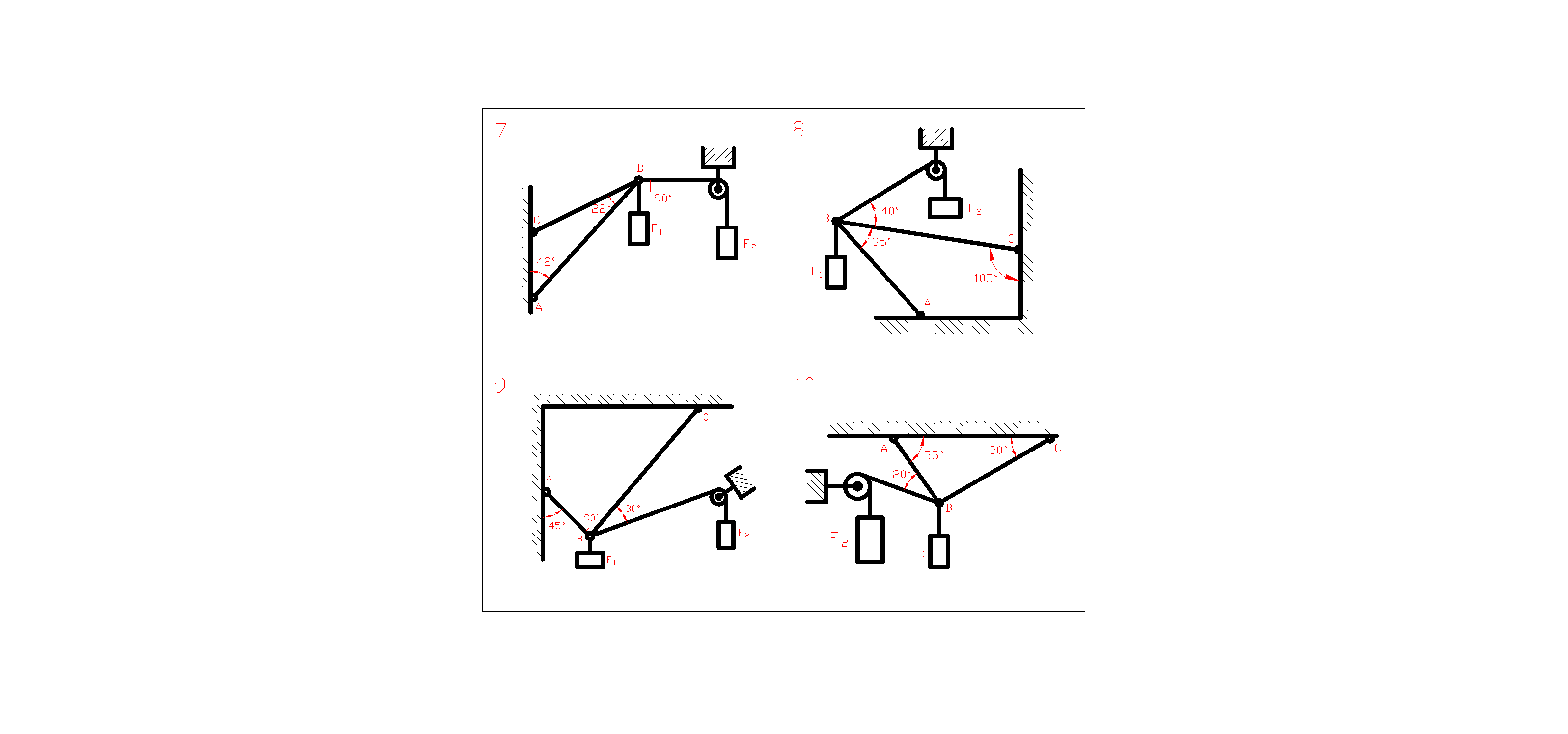
Рисунок 2
Вторую задачу (задачи 11—20) следует решать после изучения тем 1.1.1, 1.1.2.1 и 1.1.2.2. Во всех задачах требуется определить реакции опор балок. Учащимся необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротивлению материалов
|
|
|
и деталям машин.
Последовательность решения задачи:
1 Изобразить балку вместе с нагрузками.
2 Выбрать расположение координатных осей, совместив ось х с балкой, а ось у направив перпендикулярно оси х.
3 Произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом α, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную нагрузку - ее равнодействующей, приложенной в середине участка распределения нагрузки.
Рисунок 3
40свободить балку от опор, заменив их действие реакциями опор,
(рисунок 3), направленными вдоль выбранных осей координат.
5 Составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор.
6 Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.
Пример 2 Определить реакции опор балки (рисунок 3).
Решение: 1 Изобразим балку с действующими на неё нагрузками (рисунок 3).
2 Изображаем оси координат х и у.
3 Силу Fзаменяем ее составляющими Fx = F·cosα и Fy = F·sinα.
Равнодействующая q·CDравномерно распределенной нагрузки приложена в середине участка CD, в точке К(рисунок 3).
4 Освобождаем балку от опор, заменив их опорными реакциями
(рисунок 3).
5 Составляем уравнения равновесия статики и определяем неизвестные реакции опор.
Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:
Σ mА = Fу · AB + М + q·CD·AK - RD·AD = 0
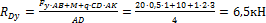
Определяем другую вертикальную реакцию:
Σ mD= RАу·AD - Fy · BD + M - q·CD · KD=0
Определяем горизонтальную реакцию:
ΣXi= RAX - Fx = 0; RAX= Fx = F·cos α = 20 · 0,866= 17,3 кН
6 Проверяем правильность найденных результатов:
ΣYi = RAy – Fy -q·CD + RDy=5,5- 10-1·2 + 6,5 =0
Условие равновесия ΣYi = 0 выполняется, следовательно, реакции опор найдены верно.
Задачи 11 — 20 Определить реакции опор двухопорной балки (рис. 4). Данные своего варианта взять из табл. 3.
|
|
|
Таблица З
| № задачи; № схемы на рис. 4 | Вариант | q, Н/м | F, Н | М, Н·м | № задачи; № схемы на рис. 4 | Вариант | q, Н/м | F, Н | М, Н·м |
| 11;1 | 10 1,5 8 4.5 | 40 25 16 50 82 15 45 18 20 54 | 10 20 14 30 60 25 40 10 25 35 | 12; 2 | 1 4.5 3.5 1.5 | 2,5 40 35 100 80 30 50 | 40 100 55 60 90 20 75 30 | ||
| 13; 3 | 02 13 24 35 | 2,5 | 80 15 30 55 | 40 | | 14; 4 | 03 14 25 36 | 10 15 12 |
| 47 52 68 73 80 91 | 8 4,5 6 3,5 | 10 100 65 85 90 20 | 15 30 45 60 18 16 | 48 53 69 74 85 92 | 16 20 | 30 25 | 24 20 | ||
| 15; 5 | 04 15 26 37 49 54 60 75 81 93 | 4,5 1,5 2,5 5,5 | 50 35 10 65 16 30 12 55 | 35 30 20 50 25 40 28 15 45 | 16; 6 | 05 16 27 38 40 55 61 76 86 94 | 3,5 0,5 4,5 8,5 | 12 10 15 18 20 | 45 10 50 30 15 25 18 30 |
| 17; 7 | 06 17 28 39 41 56 62 77 82 95 | 8 12 10 20 14 16 | 50 10 12 15 80 35 40 25 14 65 | 50 15 25 30 20 65 75 | 18; 8 | 07 18 29 30 42 57 63 78 87 96 | 6,5 2,5 1,5 | 18 24 16 20 40 35 10 12 60 15 | 15 20 12 25 50 65 25 90 35 10 |
| 19; 9 | 08 19 20 31 43 58 64 19 83 97 | 1,5 | 15 40 20 16 18 10 25 40 35 12 | 15 18 25 14 35 20 30 15 10 | 20; 10 | 09 10 21 32 44 59 65 70 88 98 | 18 20 10 16 8 14 30 | 50 65 80 10 55 30 10 | 15 150 |
Рисунок 4
Третья задача (задачи 21-30) может быть решена учащимися, если они будут ясно представлять смысл условия прочности при растяжении (сжатии)
σ = N/A ≤ [σ], где [σ]—допускаемое напряжение.
Необходимо знать, что исходя из условия прочности можно решать три вида задач:
1) проверка прочности σ = N/A ≤ [ σ]
2) проектный расчет (подбор сечения) [A ] ≥ N/[ σ]
3) определение допускаемой нагрузки [N] ≤ A· [σ]
В задачах 21-25 рассматриваются стержневые системы, работающие на растяжение и сжатие, для которых необходимо выполнить проектный расчет, а также оценить прочность выбранного стандартного сечения стержня. Стержни имеют одинаковые поперечные сечения.
Последовательность решения задачи:
1 Определить реакции стержней, используя уравнения равновесия для плоской системы сходящихся сил и проверить правильность найденных реакций.
2 Для наиболее нагруженного стержня, используя условие прочности
σ = N/A ≤ [σ], выполнить проектный расчет [A] ≥ N/[σ], определить
площадь поперечного сечения стержня, подобрать по сортаменту (ГОСТ 8509—72) подходящий номер профиля и найти стандартное значение площади поперечного сечения стержня.
|
|
|
3 Определить процент пере- или недогрузки наиболее нагруженного стержня, используя условие прочности σ = N/A ≤ [σ]], при принятых стандартных размерах площади поперечного сечения.
∆σ=σ-[σ]/[σ]·100%. Допускается недогрузка до 15% и перегрузка до 4%.
Пример 3 Для данной системы двух стержней одинакового поперечного сечения, нагруженных силой F= 170 кН (рисунок 5), определить: а) требуемую площадь поперечных сечений стержней, состоящих из двух равнобоких уголков, и подобрать по ГОСТу (см. приложение II) соответствующий профиль уголка;
б) определить процент пере- или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения, приняв [σ] =140 МПа.
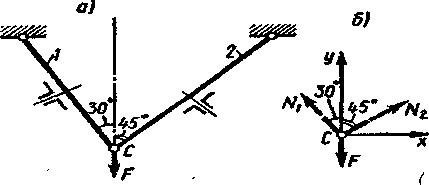
Рисунок 5
Решение: 1В данном примере в шарнире С приложена система сходящихся сил. Определяем силы N1 и N2 в стержнях 1 и 2 (рисунок 5, а), используя уравнения равновесия ΣХ=0 и ΣY=0.
ΣX = -N1·sin30° + N2·sin45° = 0 (l)
Σ Y = N1· cos30° + N2· cos45° = 0 (2)
Из(1):
N1 = N2 · sin45°/ sin30° = N2 · 0,707 / 0,5 = 1,41 (3)
Подставляем в уравнение (2) выражение (3) и получаем 1,41N2 · cos30° + N2 · cos45° - F = 0
N2 = F/1,41 - cos30° + cos45o = 170/(1,41 ·0,866 + 0,707) = 88,3kH
N1 = l,41·N2 = 1,41· 88,3 = 124 кН
2 Определяем требуемую площадь поперечного сечения для наиболее нагруженного стержня:
Nmax = N1 = 124,5 кН
Al = N1/[ σ] = 124,5 • 103/ 140 = 889 мм2 = 8,89 см2
Площадь равнобокого уголка подбираем по значению A1/2 = 8,89/2 = 4,445 см2. Используя приложение 2, назначаем профиль (L63X63X4) с площадью [А] =4,96 см2. Таким образом, требуемая площадь поперечного сечения стержней будет равна: 2·[А] =2·4,96 = 9,92 см2.
Рабочее напряжение в поперечном сечении наиболее нагруженного стержня:
σ = N1/2 · [A] = 124,5 · l03/2 · 4,96 · 102 = 125,5 Н/мм2 = 125,5 МПа
3 Проверяем прочность наиболее нагруженного стержня:
∆σ = σ -[ σ]/[ σ]·100% = 125,5 -140/ 140·100% = -10,3%
Недогрузка составляет 10,3 %,что допускается.
Задачи 21-25 Задана система двух стержней, составленных из двух равнобоких уголков (рис. 6, схемы 1–5).
При заданном значении силы F определить: 1) требуемые площади поперечных сечений стержней и подобрать по ГОСТ 8509-2 (см. приложение 2) соответствующие номера профилей; 2) определить процент пере- или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения. Принять
[σ] = 160 МПа. Данные своего варианта взять из табл. 4.
Таблица 4
| № | задачи; № схемы | F | № задачи; № схемы | |||||||||
| на рис. 6 | на рис. 6 | a | b | |||||||||
| 21;1 | 22; 2 | 23;3 | 24; 4 | 25;5 | 26; 6 | 27; 7 | 28;8 | 29; 9 | 30;10 | |||
| Варианты | кН | Варианты | м | м | ||||||||
| 0,5 | 1,5 | |||||||||||
| 1,2 | 1,8 | |||||||||||
| 0,6 | 2,4 | |||||||||||
| 0,8 | 2,2 | |||||||||||
| 1,5 | ||||||||||||
| 0,4 | 2,1 | |||||||||||
| 0,5 | ||||||||||||
| 1,4 | 1,6 | |||||||||||
| 2,3 | ||||||||||||
| 0,7 | 1,8 |
|
|
|
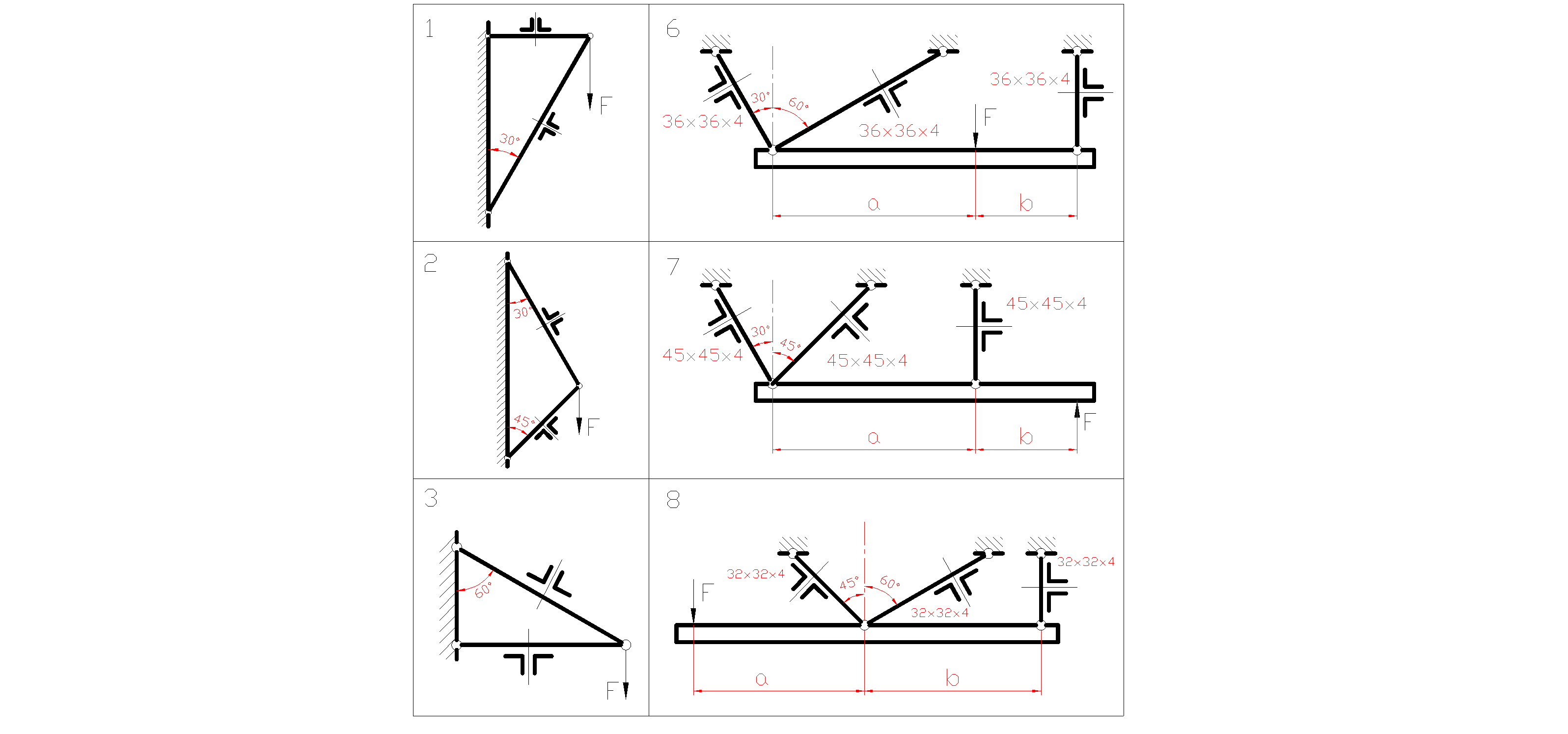
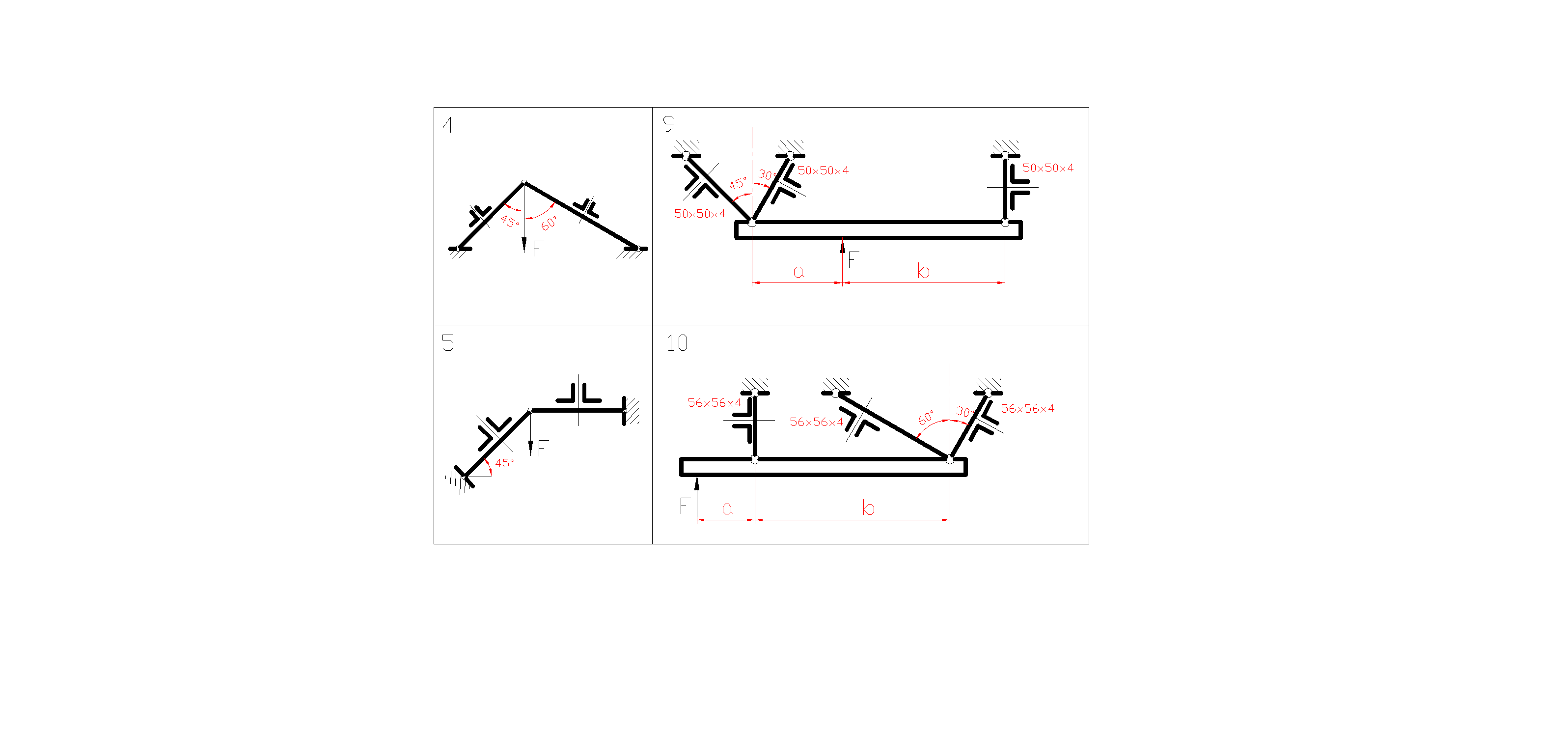Рисунок 6
В задачах 26-30 рассматривается система трех стержней одинакового поперечного сечения, поддерживающих абсолютно жесткую балку. Для наиболее нагруженного стержня следует найти допускаемое значение силы F, которая приложена к данной системе.
Последовательность решения задачи:
1 Определить силы в стержнях, используя уравнения равновесия произвольной плоской системы сил, и сделать проверку правильности найденных реакций.
2 Определить допускаемое значение силы, нагружающей систему, используя условие прочности ∆σ = N/A ≤ [σ] =>
[N] ≤ A·[σ]. Стандартное значение площади равнобокого уголка, заданного в условии задачи, взять по ГОСТу 8509—72 из приложения 2.
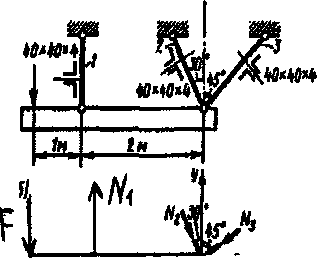Пример 4 Абсолютно жесткая балка (рисунок 7,а)поддерживается тремя стержнями одинакового поперечного сечения, представляющего собой два равнобоких уголка с размерами 40х40х4. Определить допускаемое значение силы F, если [σ] =[160] МПа. Весом балки пренебречь.
а)
Рисунок 7
Решение: 1 Выбираем расчетную схему (рисунок 7, б ), представляющую собой плоскую стержневую систему, для которой следует определить силы в стержне, используя уравнения равновесия произвольной плоской системы сил.
Σ MD = N1 · BD – F · AD= 0 (1)
Σ X = N2·sin30º - N3 · sin45° = 0 (2)
Σ MB = -F · AB + N2 · cos 30° · BD + N3 · cos 45°· BD=0 (3)
Из(1):
N1 = F · AD/ BD = F · 3/2=1,5F (4)
Из (2)
N2 = N3 · sin45°/ sin30° = N3 · 0,707/ 0,5 = 1,41 N3 (5)
В уравнение (З) подставляем вместо N2 выражение N2 = 1,41N3
-F · AB = 1,41 N3 ·cos30° · BD + N3 · cos45° · BD= 0 (6)
Из (6)
N3 = F · AB/ l,41cos30° · BD + cos45° = F · 1/1,41 · 0,866 · 2 + 0,707 · 2 = 0,26 F (7)
Подставляя (7) в (5), получаем:
N2 = 1,41N3 = 1,41 · 0.26F = 0,366F
Проверяем правильность реакций N1, N2, N3
Y= - F – N2 · cos30° - N3 · cos45° + N1 = -F - 0,366 · 0,866F - 0,26 · 0,707F + l,5F = 0
Y =0, следовательно, реакции стержней определены верно.
2 Так как все три стержня по условию имеют одинаковое поперечное сечение (рисунок 7. а), то допускаемое значение силы F определяем для наиболее нагруженного стержня, каким является стержень 1.
σ = N/A ≤ [ σ] => [N] ≤ A·[ σ]
Следовательно, Nmax= N1 = 1,5F
Исходя из условия прочности [N] = 1,5F = [σ] · 2А и учитывая, что площадь равнобокого уголка 40x40x4, А= 3,08см2 (см. приложение 2), получаем значение допускаемой силы
F = [ σ] · 2A/1,5=160 · 2 ·3,08 · 102/1,5 = 65800Н = 65,8 кН
Задачи 26-30 Задана система трех стержней, поддерживающих абсолютно жесткую балку (рис. 6, схемы 6—10). Стержни имеют одинаковое поперечное сечение, состоящее из двух равнобоких уголков заданных размеров.
Оределить допускаемое значение силы F, приняв [σ]= 160 МПа. Весом балки пренебречь. Данные своего варианта взять из табл. 4.
Четвертая задача (задачи 31-40) К решению этой задачи следует приступить после изучения темы "Изгиб". Изгиб — это такой вид нагружения
бруса, при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным: если поперечные силы не возникают, изгиб называют чистым. Изгибающий момент Ми в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно центра тяжести сечения: Ми =Σm. Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на отсеченную часть: Q = ΣF. Причем все внешние силы и моменты действуют в главной продольной плоскости бруса и расположены перпендикулярно продольной оси бруса.
Правило знаков для поперечной силы: силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки, приписывается знак плюс (рисунок 8, а), а силам поворачивающим отсеченную часть балки относительно рассматриваемого сечения против хода часовой стрелки, приписывается знак минус (рисунок 8,6).
Правило знаков для изгибающих моментов: внешним моментом изгибающим мысленно закрепленную в рассматриваемом сечении отсечённую часть бруса выпуклостью вниз, приписывается знак плюс (рисунок 9, а), а моментам, изгибающим, отсеченную часть бруса выпуклостью вверх, — знак минус
(рисунок 9,б).
Между изгибающим моментом Мx. поперечной силой Qy и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости:
dMx/dz=Ov; DQv/dz=q
На основе метода сечений и дифференциальных зависимостей устанавливается взаимосвязь эпюр Мx и Qy, между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (включая опорные сечения), а также сечения, ограничивающие участки с равномерно распределенной нагрузкой.
|
Рисунок 8 Рисунок 9
Приведем некоторые правила построения эпюр.
Для эпюры поперечных сил:
1 На участке, нагруженном равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки.
2 На участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки.
3 В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет значения.
4 В сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно на значение, равное приложенной силе.
5 В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.
Для эпюры изгибающих моментов:
1 На участке, нагруженном равномерно распределенной нагрузкой, эпюра моментов изображается квадратичной параболой. Выпуклость параболы направлена навстречу нагрузке.
2 На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией.
3 В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется скачкообразно на значение, равное моменту приложенной пары.
4 Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в концевом сечении приложена активная или реактивная пара сил, то изгибающий момент в сечении равен моменту приложенной пары.
5 На участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки.
6 Изгибающий момент принимает экстремальное значение в сечении, где эпюра поперечных сил проходит через нуль, меняя знаки с "+" на "-" или с "-" на "+".
В рассматриваемой задаче требуется построить эпюры поперечных сил и изгибающих моментов, а также подобрать размеры поперечного сечения балки, выполненной из прокатного профиля - двутавра.
Условие прочности для балок с сечениями, симметричными относительно нейтральной оси, имеет вид:
σmax = MXmax./ Wx ≤ [ σ],
где Wx — осевой момент сопротивления сечения.
Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимое значение осевого момента сопротивления: Wx ≥ MXmax / [σ].
По наибольшему моменту сопротивления Wx, подбирают соответствующее сечение по сортаменту (см. приложение 1).
Для закрепленной одним концом балки строить эпюры целесообразно со свободного конца (чтобы избежать определения опорных реакций в заделке).
Последовательность решения задачи:
1 Балку разделить на участки по характерным сечениям.
2 Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.
3 Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов.
4 Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т. е. определить Wx в опасном сечении, где изгибающий момент имеет наибольшее по модулю значение.
Пример 5 Для заданной консольной балки (поперечное сечение- двутавр, [σ] =160 МПа) построить эпюры Qy и Мx и подобрать сечение по сортаменту.
Решение: 1 Делим балку на участки по характерным сечениям А, В, С (рисунок 7, а).
2 Определяем значения поперечной силы Qy в характерных сечениях и строим эпюру (рисунок 10,б):
Рисунок 10
3 Определяем значения изгибающего момента Мх в характерных сечениях и строим эпюру (рисунок 10, в):
Ма = 0
МпрВ = F2· AB= 1 · 3 = 3 кН·м
МлевВ = F2 · AB + M = 1 · 3 + 12 =1 5 кН·м
Мпрс = F2 ·AC + M - F1 · BC = l · 5 + 12-2 · 2 = 13 кН·м
4 Исходя из эпюры Мх (рисунок 8, в)
Мхтах= 15 кН·м = 15·106 Н·мм
Wх = Мхтах / [σ]=15·106/ 160= 93700 мм3 = 93,7 см3
В соответствии с ГОСТ 8239—72 выбираем двутавр № 16, Wx= 109 см3 (см. приложение 1).
Тогда
σ = 15·106/ 109·102 = 136,7 МПа
Определяем процент загрузки:
∆σ =136,7-160 /160 ·100% = -14% недогрузки, что допускается.
Задачи 31 - 40 Для стальной балки, жестко защемленной одним концом и
нагруженной, как показано на рис. 11 (схемы 1—10), построить эпюры
поперечных сил и изгибающих моментов. Определить из условия прочности
необходимый размер двутавра, считая [σ] = 160 МПа. Данные своего варианта
взять из табл. 5.
Таблица 5
| •№зада-чи; № схемы на рис. 11 | Вари- ант | F1 | F2 | М | № задачи; № схемы на рис.11 | Вариант | F1 | F2 | М | ||||||||
| кН | кН • м | кН | кН • м | ||||||||||||||
| 31;1 | 1 2 3 4 4 5 6 7 7 9 | 2 2 3 4 4 5 6 6 | 32;2 | 15 26 32 42 51 65 77 88 99 | 1,5 2. 2,5 | 1,5 | 6 8 3 6 2 3 | ||||||||||
| 33;3 | 02 14 29 35 49 53 62 74 82 98 | 2 2,5 | 1.5 1,5 1,5 | 2,5 | 34;4 | 03 17 28 34 40 63 72 86 91 | 2,5 3 3,5 6 | 10 14 16 15 20 30 25 35 | |||||||||
| 35;5 | 05 16 | 2 4 8 6 4 6 1 6 3 | 6 3 1 3 5 2 8 5 6 1 | 10 12 20 15 18 30 16 32 14 | 36;6 | 04 19 20 36 43 54 61 78 89 93 | 5 6 8 5 4 6 4 1 10 | 2 3 5 2 5 6 | |||||||||
| 37,7 | 1,5 | 38;8 | |||||||||||||||
| 1,5 | 2,5 | ||||||||||||||||
| 0,5 | |||||||||||||||||
| 3,5 | |||||||||||||||||
| 1,5 | |||||||||||||||||
| 2,5 | |||||||||||||||||
| 39;9 | 40;10 ;10 | ||||||||||||||||
| 1,5 | |||||||||||||||||
| 2,5 | |||||||||||||||||
| 1,5 | |||||||||||||||||
| 2,5 | |||||||||||||||||
Рисунок 11
Пятая задача (задача 41 — 50) Для того чтобы решить пятую задачу, необходимо внимательно изучить тему "Изгиб", методические указания к задаче 4, а также приведенный далее пример.
Последовательность решения задачи та же, что и четвертой. Отличие лишь в том, что пятую задачу начинают решать с определения реакций опор балки и проверки правильности найденных реакций.
Пример 6 Для заданной двухопорной балки (рисунок 12, а) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h,b,d) вформе прямоугольника или круга, приняв для прямоугольника h/b= 1,5. Считать [σ] = 160 МПа.
Решение: 1 Определяем опорные реакции и проверяем их найденные значения:
МD = 0; MD = -M1+F2 · CD + M2+RВ · BD-F1 ·OD=0
RB = M1 - F2 ·CD+F1 · OD/BD=(20-30 · 10+18 · 15)/ 10=10кН
MВ = 0; MВ = F1 · OB+M2-F2 ·BC-RD · BD-M1=0
Rd = (-F1 ·OB+M2 –F2 ·ВС-M1)/BD=(-18-5+10-30 · 4-20)/10=-22кН
Так как реакция RD получилась со знаком минус, то изменяем ее первоначальное направление на противоположное. Истинное направление реакции RD - вниз (рисунок 12, б).
Проверка: Y0= - F + RB +F2 - RD = - 18+ 10 + 30 - 22 = 0. Условие статики
Yi = 0 выполняется, следовательно, реакции опор определены верно. При построении эпюр используем только истинные направления реакций опор.
2 Делим балку на участки по характерным сечениям О, В, С, D (рисунок 12,6).
3 Определяем в характерных сечениях значения поперечной силы Qv и строим эпюру слева направо (рисунок 12, в):
Qnpo = -F1 = -18кН
Q леB = -F1 = -18кН
Q"pb = - F1 +RB= -18 + 10 = -8кН
Qлев с = -F1 + RВ + F2 = -18+10+30 = 22кН
Q левD = - F1 + RB +F2 = 22кН
4 Вычисляем в характерных сечениях значения изгибающего момента Мх и строим эпюру (рисунок 12, г):
Мо = 0
МВ = - F1 · АВ = - 18 · 5 = - 90кН · м
Mлевс= - F1 · ОС + RB · BC= -18·9+10·4 = -122кН·м
Mпрс =.-F1· ОС + RB ·BC + М2 = -18 · 9+10 · 4+10= -112 кН ·м
Mлевс = - F1 · OD+ RB ·BD + М2 +F1 · CD= -18 · 15+10 · 10 + 10 + 30 · 6 = 20 кН · м
5 Вычисляем размеры сечения данной балки из условий прочности на изгиб по двум вариантам: а) сечение – прямоугольник с заданным соотношением сторон (рисунок 12, е); б) сечение – круг (рисунок 12, д). Вычисление размеров прямоугольного сечения:
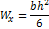
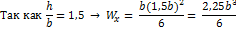
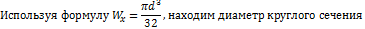
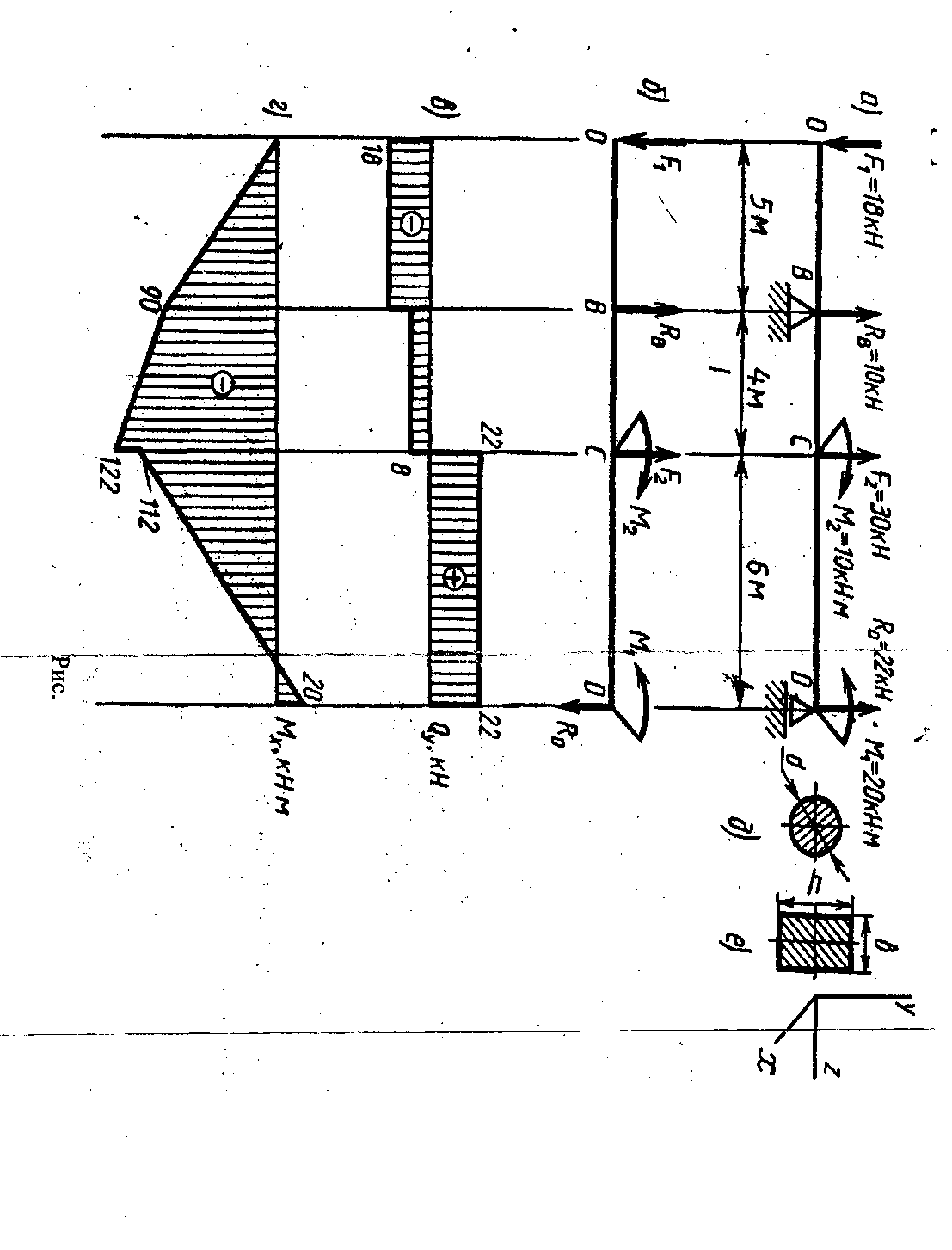
Рисунок 12
Задачи 41-50 Для заданной двухопорной балки (рис. 13, схемы 1 —10)
определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Подобрать из условия прочности размеры поперечного сечения прямоугольника (задачи 41,43,45,47,49) или круга (задачи 42,44,46,48,50), приняв для прямоугольника h= 2b. Считать [σ] =150 МПа, данные своего варианта взять из табл. 6.
Таблица 6
| № за-дачи; | Вариант | F1 | F2 | М | № за-дачи; | Вари ант | F1 | F2 | М | |
| кН | кН·м | кН | кН·м | |||||||
| №схе- | №схе- | |||||||||
| мы на | мы на | |||||||||
| рис.13 | рис.13 | |||||||||
| 41;1 | 42;2 | |||||||||
| 43;3 | 44;4 | |||||||||
| ■ | ||||||||||
| 45;5 | 05 19 | 20 15 | 2 3 | 46;6 | 04 18 | 3 5 | 2 4 | 10 8 | ||
| 1,5 | 0,6 | |||||||||
| 3,5 | 2,4 | |||||||||
| 2,5 | 1,6 | |||||||||
| 0,6 |
|
|
|
