Эффекты типов интенсивности

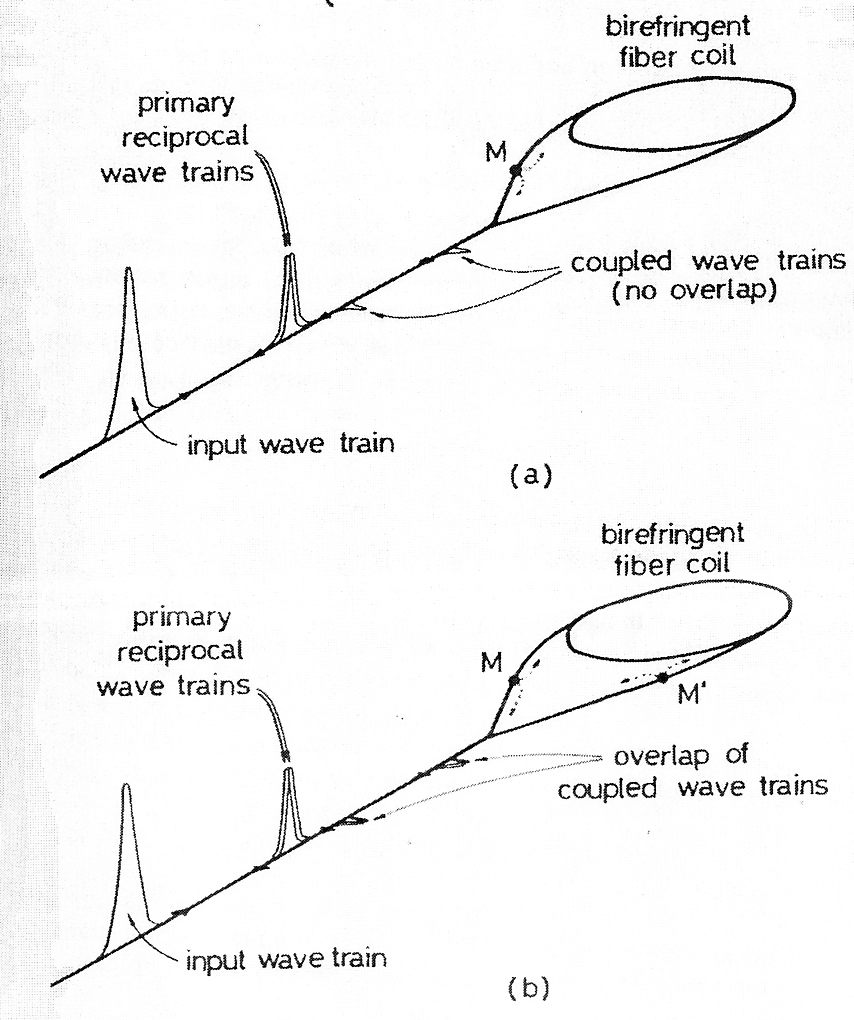
Рассмотрим сначала кольцевой интерферометр, использующий сохраняющие поляризацию волокна или волновод с идеальным вводом, то есть состояние поляризации источника света сохраняется на входе в той же моде, моде 1 и, в частности, выравнивается передача моды поляризатора. Когда имеется один поляризатор с точкой связи М в катушке, ввод волнового импульса от широкополосного источника дает на выходе два первичных волновых импульса, которые по-прежнему в моде 1 и которые прекрасно в фазе в связи с взаимностью. Есть также два связанные волновые мимпульсы в моде 2, которые распространяются вдоль различных путей (Рисунок 5.2(a)). Это должно стимулировать разность фаз, но, в связи с их короткой длиной когерентности, они не перекрываются и эти паразитные помехи потеряют свою контрастность (за исключением контакта в середине катушки, которым на данный момент можно пренебречь) [4].

При наличии двух точек связи M и M', размещенных на одинаковом расстоянии от разделителя (Рисунок 5.2(b)), поперечно связанные волновые импульсы пересекаются и интерферируют [5,6]. Это похоже на проблему обратного отражения, в которой одна точка отражения не вредна, но две точки симметричного отражения дают паразитную интерференцию Михельсона. На самом деле имеется шесть волновых импульсов:

· Два основных взаимных волновых импульса в одной фазе, накопленные в распространяющейся вдоль длины L катушки:

 

Ф₁₁₁ = Ф'₁₁₁ = β₁ L

 

где β₁ − константа распространения моды 1.

 

· Два вторичных волновых импульса, распространяемых в моде 1 между разделителем и точками связи и которые связаны в моде 2 для остальной части распространения. Их соответствующие фазы

Ввод серии волн

Перекрытые пары волновых импульсов

Ввод серии волн

Основная обратная величина волновых импульсов

Основная обратная величина волновых импульсов

Волоконная катушка с двой- ным лучепреломлением

Волоконная катушка с двой- ным лучепреломлением

Пары волновых импуль- сов (не перекрытые)

Рисунок 5.2. Распространения волновых импульсов в сохраняющем поляризацию кольцевом интерферометре: (a) с одним перекрестным устройством связи в точке М; (б) с двумя симметричными точками связи в точках M и M'

(5.3)

, (5.4)

 

где β₂ − константа распространения моды 2, L_M − расстояние между разделителем и M, L_MМ' − расстояние между M и M ', и L_M - это расстояние между разделителем и M'.

· Два других вторичных волновых импульсов распространяются в моде 1 между разделителем и точками связи, а также между двумя точками связи, и которые были связаны в моде 2 между точками связи и разделителем на выходе. Их соответствующих фазы

 

(5.5)

(5.6)

 

Обе пары вторичных волновых импульсов имеют те же ложные разности фаз:

(5.7)

 

Обратите внимание, что распространение между двумя точками связи не дает никакой несогласованной разности фаз. Несогласованность связана только с разностью в накопленном двулучепреломлении между разделителем и обеими симметричными точками связи.

Эти две пары когерентных волновых импульсов с пересеченной модой 2 на выходе и являются ослабленным поляризатором. Поэтому сигнал фазовой ошибки идет от эффекта типичной интенсивности, и это снижает отклонение интенсивности соотношением поляризатора:

 

, (5.8)

 

где ρ _М и ρ _M' – интенсивности поперечно пересеченных отношений на M и M'. Поскольку может изменяться с периодом 2π, среднее значение этой фазовой ошибки равно нулю, и это rms − отклонение

 

(5.9)

 

Обратите внимание, что существуют дополнительные волновые импульсы, которые испытывают пересекающиеся связи дважды, на входе и на выходе. Они возвращаются в той же моде 1 и в той же фазе, в связи с взаимностью

(5.10)

 

Когда имеется несколько пар симметричный связанных точек, каждая пара создает две паразитные интерференционные волны, и поскольку эти волны не когерентны друг с другом, ложные сигналы просто добавляются к интенсивности.

Это позволяет оценить эффект от волоконной катушки с простой моделью [6]. Случайные связи вдоль катушки могут рассматриваться как созданные дискретные точки M_i для каждой длины деполяризации L_d (Рисунок 5.3) с интенсивностью связи h · L_d. В катушке длиной L, имеется N = L/L_d точек связи и N /2 пар симметричных точек. Каждая пара создает две пары

Рисунок 5.3. Простая модель пар симметричных перекрестных отдельных точек связи Mi и Mi ' для каждой длины деполяризации Ld.

Пара

вторичных волновых импульсов (в каждом направлении), которые дают ту же ошибки отклонения фазы; поэтому,

 

, (5.11)

 

поскольку h · L_d интенсивность отношения между основными волновыми импульсами и вторичными перекрестными волновыми импульсами. Разность фаз случайным образом распределенная через 2π и общий эффект определяется суммированием независимых случайных величин 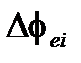, которые центрируются около нуля. Таким образом, среднее значение фазовой ошибки 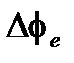также ноль и площадь ее rms отклонения равна сумме квадратов rms отклонений каждой переменной:

(5.12)

 

У нас есть , так как среднее значение есть 1/2; поэтому,

так как L=N·L_d и

,

 

где h·L− общее сцепление поляризации вдоль катушки. Среднеквадратическое отклонение фазовой ошибки двулучепреломления волоконной катушки не пропорционально поляризационному соотношению связи h·L в катушке, как может сначала показаться. Это снижение пропорционально корню числа N поляризационной длины вдоль катушки [6].

Например, для типичного деполяризатора длиной 10 см, N равно 10⁴ в 1 км катушки. Поскольку сохранение обычно составляет 20 дБ/км, есть 10⁴ точек связи 60 дБ, которые дают перед фильтрацией по поляризатору общую фазовую ошибку (rms значение) только 10⁻⁴ рад, не 10⁻² рад. Поляризатор со смещением 30 дБ является достаточным для того, чтобы уменьшить типичную интенсивность ошибки смещения ниже 10⁻⁷ рад. Это значение 30 дБ, должно сравниваться с 140 дБ, которые потребовались бы без сохранения поляризации и деполяризационного эффекта!

Этот результат относится только к сцеплениям, которые постоянно распределяются вдоль волоконной катушки, случайные соединения в настоящее время рассматривается как стационарный стохастический процесс. Однако на практике главным ограничивающим фактором, является не сама катушка, а локализованные соединения на обоих концах катушки. Фактически в предыдущем примере эффект волоконной катушки эквивалентен паре симметричных точек с 40 дБ поперечной поляризацией, даже если общее сохранение катушки только 20 дБ. Чтобы сохранить это преимущество, желательно для управления поляризацией контролировать поперечные соединения на концах катушки лучше, чем значение 40 дБ.

В многоволоконной конфигурации возникают проблемы с сохранением поляризации в устройстве связи катушки, это, как правило, в диапазоне от 20 до 30 дБ. Есть другие паразитные связи на сшиваниях между началами и концами катушки, но возможен дисбаланс длины обоих проводящих устройств связи. Если их асимметрия больше, чем длина деполяризации (т.е. обычно 10 см), когеренция между этими ложными волнами подавлена.

В цепи интегральной оптики, поляризационное соединение на разветвителе (с Y-соединением в частности) является незначительным, поскольку сильное двулучепреломление LiNbО₃ обеспечивает сохранение отличной поляризации. Паразитные взаимодействия исходят от концов катушки в стыках соединений цепи. 40 ДБ соединения только 0,5 град несооосности основных осей; вместе с тем на практике трудно иметь прочное подключение волокна без возбуждения напряжений, обеспечивающих локальное дополнительное двулучепреломление и таким образом остаточную поперечную поляризацию. Длина деполяризации в LiNbО₃ гораздо меньше, чем в волокне (около 500 мкм вместо 10 см, поскольку разность показателей двулучепреломления 8·10^–2 вместо 5·10^–4), но это все еще слишком много, чтобы получить достаточный дисбаланс между обеими ветвями Y-соединения. Фактически, типичными значениями разделения ответвлений являются 200 мкм и угол наклона 10 град для цепи в форме параллелограмма, т.е. дисбаланс только 200 мкм x tan10 град = 35 мкм по сравнению с деполяризацией длиной 500 мкм.

Это показывает, что это очень важно, точно контролировать масштабы и положение различных локализованных поперечных поляризаций, даже если они кажутся похороненными в общей системе устройства поперечного соединения. Заметим, однако, что эти эффекты типа интенсивности далее могут быть сокращены на втором поляризаторе, размещенном как детектор, поскольку они переносятся волнами, которые поляризованы поперечно относительно к основным начальным волнам.

 

5.2.2. Комментарий о длине деполяризации L_d

против длины корреляционной поляризации L_pc

 

Как объясняется в приложении 1, контрастность или видимость интерференционных полос равна автокорреляционной функции γ _с центрального спектра. Большинство обычно анализируют проблемы, независимо от точной "колоколообразной формы" функции, с половинной шириной функции, называемой временем когерентности τ _с или соответствующей длиной когерентности L_c = с τ _с. Как указывается в разделе 5.1, их точное нахождение не всегда точно определено, и это заслуживает более точного переопределения.

Классическое определение [3] аналогично нормальному квадратичному усреднению, с использованием γ _с как распределение вероятностей:

 

(5.13)

 

где – оптическая разность хода. Таким образом, длина когерентности является среднеквадратическим половиной ширины от γ _с или это половина ширины от 1σ, σ – стандартное отклонение. Это определение является наиболее важным в классической интерферометрии, поскольку проблема обычно в определении длины, которая сохраняет хороший контраст интерференции.

Как мы уже видели, длина, которая подавляет контраст, также является очень важной: можно назвать длину декогеренции . Поскольку, в теории, функция колоколообразной автокорреляция достигает нуля асимптотически в бесконечности, она должна быть бесконечной; но, на практике полуширина 4σ является значительной. Эта длина декогерентности определяется просто как

(5.14)

 

где – средняя длины волны широкого спектра и является ее полной шириной на половине максимума.

Когда волновой пакет используется для анализа эффекта, то должен рассматриваться вопрос о том, что является их полной шириной, поскольку по всей ширине автокорреляции пульсации удваиваются и этот импульс по всей ширине.

Применяя эти понятия к проблеме деполяризации в двулучепреломляющей среде, кажется более подходящим соотнести длину деполяризации с длиной декогерентности . В частности, обеспечение двух узлов соединения с перекрестной поляризацией не дает каких-либо ложных сигналов, их несоответствие должно быть равно или больше, чем , с этим последним определением. Если использовать , сигнал по-прежнему 80% от совершенно контрастного случая. Кажется, больше подходит называть длиной корреляционной поляризации с

 

Это длина распространения в двулучепреломляющей среде, которая сохраняет хорошую степень поляризации (т.е. хорошее статистическое соотношение между обоими ортогональными компонентами поляризации).

Вариант случайного соединения вдоль катушки является более сложным. В разделе 5.2.1 мы рассматривали число N длины деполяризации вдоль волокон, которая дает верхнюю оценку предела фазовой ошибки. Однако мы хотим достичь более точной количественной оценки воздействия и, в частности, определить фактическую половину ширины, которая может быть использована. В любом случае, если бывает более подходящей, чем , это умножает на четыре число элементов в среднем, которая дает фазовую ошибку, которая в раза ниже, чем ранее найденная.

Это позволяет использовать модель путем деления волокна катушки на элементарные сегменты длиной L_е, которые меньше, чем длина деполяризации L_d, но, по-прежнему длиннее ширины автокорреляции стохастических перекрестных процессов соединений в волокнае, которые предполагаются очень короткими (Рисунок 5.4). Принимая два симметричных элементарных сегмента, они уступают ошибке наклона фазы:

 

Рисунок 5.4. Усовершенствованная модель с элементарным сегментом Lе.

 

(5.15)

 

Фактор 2 принимает в расчет ввод и вывод пересекающихся соединений и - отношение интенсивностей пересекающихся соединений вдоль L_e. Тем не менее, элементарный сегмент i дает ложный сигнал не только со своим симметричным сегментом i, но также и с другими сегментами j, которые являются вокруг этого сегмента симметрично. По сравнению с симметричным случаем ошибки уменьшается пропорционально автокорреляционной функции γ _с:

(5.16)

 

где – значение для фактической разности хода между этими двумя слегка несбалансированными сегментами. Подобно анализу в разделе 5.2.1 общая фазовая ошибка является случайной величиной, которая складывается из независимых переменных . Поскольку равномерно распределены по 2π, они все центрированы около нулевого среднего значения и площади среднеквадратичного отклонения представляет собой сумму квадратов среднеквадратичных отклонений всех этих независимых переменных:

(5.17)

 

Для данного элемента i, мы сначала возьмем сумму за j. Фактически, различные независимы, поскольку предполагается, что L_е длиннее ширины автокорреляции со стохастическими процессами поперечных соединений в волокне, и

(5.18)

 

Заменяя дискретные суммирования интегрированием, имеем

 

(5.19)

 

Мы вводим новую длину корреляционной поляризации с

(5.20)

и

(5.21)

Мы имеем сейчас сумму по i (т.е. сегментов на половину катушки) и

(5.22)

 

По сравнению с результатами анализа раздела 5.2.1, заменяет L_d. В конкретном случае гауссовской автокорреляции, могут быть легко вычислены, с . Установлено, что

 

(5.23)

 

Этот утонченный анализ показывает, что длина , которая дает точное число элементов в среднем вдоль катушки, является промежуточным значением между длиной деполяризации L_d и длиной корреляционной поляризации L_pc; но в любом случае ошибки наклона фазы, вызванные в волоконной катушке со стационарными случайными поперечными соединениями, остаются очень похожими на ошибки простого анализа в разделе 5.2.1.

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: