 |
Использование сдвига частоты
|
|
|
|
Впервые было предложено использовать механизмы функционирования закрытой рабочей петли генерацией сдвига частот с акусто-оптической модуляцией (AOM) в так называемых Брэгговских решетках [1,2]. Фактически эффект Саньяка может быть истолкован как эффект Доплера на катушке с разделением лучей (см. раздел 2.1.1). Таким образом, частота сдвигов позиций, помещенных в начале катушки, может обнуляться доплеровским сдвигом эффекта Саньяка. Абсолютная фаза  , накопленная в распространении, является
, накопленная в распространении, является
 (8.2)
(8.2)
где f – временнáя частота волны. Затем обратная связь сдвигает частоту  , создавая обратной связью разность фаз
, создавая обратной связью разность фаз  :
:
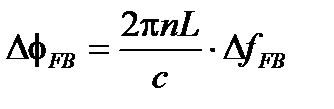 (8.3)
(8.3)
Теперь новое измерение  линейно зависит скорости вращения Ω:
линейно зависит скорости вращения Ω:
 (8.4)
(8.4)
Чтобы получить высокую чувствительность, сигнал ошибки получается с дополнительным фазовым модулятором и использованием схемы модуляции-демодуляции, схемы открытой петли [3].
Однако, чтобы охватить весь динамический диапазон этой обратной связи, сдвиг частоты  должна меняться около нуля между плюсом и минусом в пределах несколько сотен килогерц. Поскольку акусто-оптические модуляторы работают только на высоких центральных частотах (как правило, 50-100 МГц) с относительной пропускной способностью в несколько процентов, это требует использования двух ячеек для получения обратной связи с разницей в сдвиге частот
должна меняться около нуля между плюсом и минусом в пределах несколько сотен килогерц. Поскольку акусто-оптические модуляторы работают только на высоких центральных частотах (как правило, 50-100 МГц) с относительной пропускной способностью в несколько процентов, это требует использования двух ячеек для получения обратной связи с разницей в сдвиге частот  . Они могут быть помещены противоположно на одном конце катушки, первая ячейка генерирует смещение вверх, а вторая – смещение вниз (Рисунок 8.2(a)), или же они могут быть размещены на обоих концах катушки с постоянной центральной частоте fc, создавая постоянный сдвиг длины волны с такими же знаками смещения (Рисунок 8.2(b)). Один эксплуатируется на
. Они могут быть помещены противоположно на одном конце катушки, первая ячейка генерирует смещение вверх, а вторая – смещение вниз (Рисунок 8.2(a)), или же они могут быть размещены на обоих концах катушки с постоянной центральной частоте fc, создавая постоянный сдвиг длины волны с такими же знаками смещения (Рисунок 8.2(b)). Один эксплуатируется на  , и другой эксплуатируется на контролируемой частоте fc +
, и другой эксплуатируется на контролируемой частоте fc +  , создавая сдвиг длины волны
, создавая сдвиг длины волны  +
+ 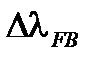 . Когда гироскопа в покое, обратная связь сдвига частоты
. Когда гироскопа в покое, обратная связь сдвига частоты  в идеале стремится к нулю, но внутренние одномодовые обратимости это стремление нарушают [4]. Учитываем сначала симметричный случай (рис 8.2(b)), источник испускает волны длиной λ, но это фактическая длина противонаправленных волн:
в идеале стремится к нулю, но внутренние одномодовые обратимости это стремление нарушают [4]. Учитываем сначала симметричный случай (рис 8.2(b)), источник испускает волны длиной λ, но это фактическая длина противонаправленных волн:
|
|
|


| Волоконная катушка |
| Волоконная катушка |
| Разделитель |
| Разделитель |
| λ |
| (а) |
| Рисунок 8.2. Схема замкнутой петли с двумя модуляторами акустико-оптических частот (AOM): (а) модуляторы расположены последовательно; (b) модуляторы на обоих концах катушки |
| (b) |
• λ между разделителем и модуляторами на входе;
• λ +  между обеими модуляторами;
между обеими модуляторами;
• λ +  между модуляторами и разделителем на выходе.
между модуляторами и разделителем на выходе.
Обе противонаправленные волны сохраняют ту же длину λ +  между обоими модуляторами, но они имеют разность
между обоими модуляторами, но они имеют разность  между разделителем и модуляторами. Это различие в длине между противоположными волнами дает несогласованную разность фаз
между разделителем и модуляторами. Это различие в длине между противоположными волнами дает несогласованную разность фаз  когда они распространяют между разделителем и первым модулятором, и другую несогласованную разность фаз с противоположным знаком
когда они распространяют между разделителем и первым модулятором, и другую несогласованную разность фаз с противоположным знаком 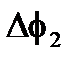 между разделителем и вторым модулятором. Когда расстояние между разделителем и каждым модулятором точно равны, общая несогласованная разность фаз
между разделителем и вторым модулятором. Когда расстояние между разделителем и каждым модулятором точно равны, общая несогласованная разность фаз  +
+ 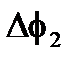 обнуляется, но небольшой дисбаланс
обнуляется, но небольшой дисбаланс  в точности симметрии двух модуляторов выдает остаточную фазовую ошибку:
в точности симметрии двух модуляторов выдает остаточную фазовую ошибку:
 (8.5)
(8.5)
Для типичной центральной частоты fc около 100 МГц эта несогласованная фазовая ошибка достигает более, чем 2 мкрад/мкм.
Когда два модуляторами помещаются в оппозиции на одном конце катушки (Рисунок 8.2(a)), аналогичный результат получается, когда  теперь представляет собой расстояние между обоими модуляторами. Есть такая же проблема стабильности, но также имеется константа смещения, связанная с усреднением значения
теперь представляет собой расстояние между обоими модуляторами. Есть такая же проблема стабильности, но также имеется константа смещения, связанная с усреднением значения  .
.
|
|
|
Было предложено несколько решений для повышения механической стабильности этой сборки, включая двойные Брэгговские решетки, в которых смещения обоих частот объединены в той же компоненте [5] и в реализации интегральной оптики [6], но этот подход замкнутой петли с акустико-оптическим смещением частиоты сложен технологически и потребляет сравнительно высокую мощность. Кроме того, даже с улучшением стабильности эти подходы не соблюдают согласованность. Обратите внимание, что эта чувствительность к дисбалансу модуляторов была предложена как метод обнаружения любых эффектов, которые затрагивают этот дисбаланс [7].
|
|
|


