Магнитно-оптический эффект Фарадея

Даже в прекрасно взаимной системе фазовый сдвиг Саньяка не только точный эффект необратимости. В частности благодаря магнитно оптическому эффекту Фарадея продольное магнитное поле В изменяет фазу циркулярно поляризованной волны, суммарно определяемой коэффициентом Верде V среды. Знак этого фазового сдвига зависит от левой или правой руки характера круговой поляризации, а также от относительного направления поля и вектора распространения света. Хорошо известно, что этот фазовый сдвиг может проявить себя как изменение 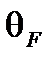в ориентации линейно поляризованного света, вытекающей из противоположного сдвига фаз сораспространяющегося лево- и праворучных циркулярно-поляризованных компонентов: 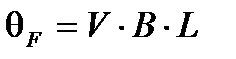, где L – длина среды. Также она может определяться как разность фаз 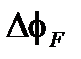в кольцевом волоконном интерферометре, в котором идентичные циркулярно поляризованные волны противонаправлены вокруг катушки (Рисунок. 7.1). Как показано в приложении 1, эта разность фаз равна двойному углу поворота Фарадея :

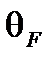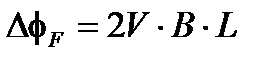(7.1)

 

Сначала кажется, что общий эффект Фарадея по всему контуру пропорционален линейному интегралу от В по этому контуру. Для замкнутого контура результат должен быть отличен от нуля согласно закону Ампера, только если этот контур включает проводящий электрический ток. Конфигурация тороидального замкнутого контура была использована для демонстрации электрического тока в волоконном датчике [1], но волоконно- оптический гироскоп не должны быть чувствительным к магнитным полям окружающей среды, из-за отсутствия пересекающихся электрических токов. Однако это действительно верно, только если состояние поляризации сохраняется вдоль волокна. Фазовый сдвиг Фарадея, накопленный вдоль вектора элементарной длины dz, является

 

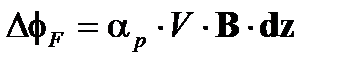(7.2)

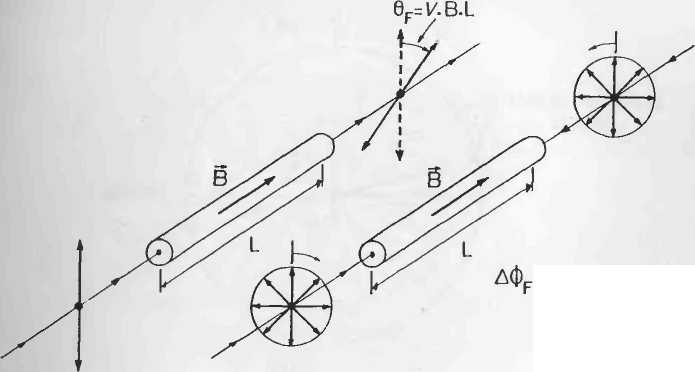
Рисунок 7.1. Эффект Фарадея: (а) вращение при линейной поляризации; (b) разность фаз между двумя противонаправленными круговыми поляризациями

ΔФF=2 V· B·L

(a)

(b)

где – коэффициент, который зависит от состояния поляризации. Он равен нулю для линейной поляризации и ± 1 для круговых поляризаций. Он имеет промежуточные значения для эллиптических поляризаций. Общая разность фаз между обеими противонаправленными волнами представлена соотношением

 

(7.3)

 

которое может быть отличным от нуля, даже если линейный интеграл равен нулю, поскольку не постоянна. Это связано с изменением поляризации вдоль волокна, вытекающее из остаточного двулучепреломления [2,3,4]. Конфигурации, использующие двулучепреломление, вызванное изгибом, повышают чувствительность к внешним магнитным полям, что продемонстрировано на магнитометре с кольцевым интерферометром [5].

Если предположить, что влияние магнитного поля земли B _земли было проинтегрировано конструктивно вдоль всего волокна длиной L, максимальная взаимообратная разность фаз будет

 

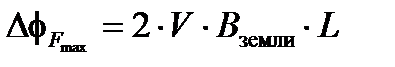(7.4)

 

Постоянная Верде V имеет зависимость от длины волны λ^–2 равна 2 рад·м^–1·Т^–1 на 0,85 мкм, а B _земли обычно составляет 0,5G (или 5·10^–5 Тесла), 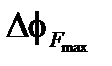будет достигать 0,2 рад на 1 км длины катушки. Экспериментально было отмечено [2-4], что существует фактор компенсации примерно 10³ в гироскопе, использующем обычное волокно, который дает погрешность измерения, приблизительно эквивалентную скорости вращения земли (т.е. 15 град/ч).

Обратите внимание, что эффект Фарадея также приводится в научной и учебной литературе в зависимости от поля Н. Поскольку в диамагнитных материалах, подобных кремнезему, В и Н пропорциональны, и относительная магнитная проницаемость близка к единице, единица измерения постоянной Верде V достигается путем умножения его "B-значение" при 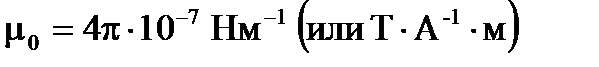; то есть «H- значение» V это 2,5·10^–6 рад А ^–1 на длине волны от 0,85 мкм.

Использование сохраняющего поляризацию волокна очень полезно для уменьшения необратимости, вызываемой двулучепреломлением, также для уменьшения магнитной зависимости, и на практике остаточная фазовая ошибка Фарадея становится порядка 1 мрад для 1 G (10^–4 Тесла). Однако эффект не является полностью обнуляющим вне связи с остаточным вращением осей двулучепреломления практических волокон [6]. Этот имеющийся опыт очень высоких напряжений, которые, как правило, дают геликоидальную фигуру для напряженных стержней, и вызванного напряжениями высокого двулучепреломления волокон, используется для сохранения поляризации с медленно меняющейся ориентацией их основных осей [7].

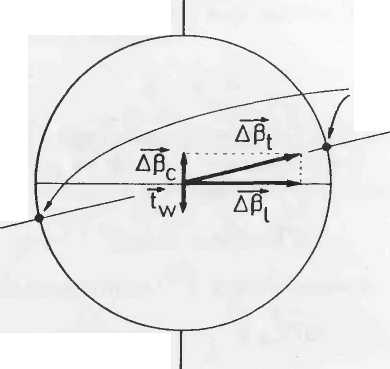
Когда поворачиваются основные оси в волокне с линейным двулучепреломлением, собственные моды поляризации не находятся в состоянии линейной поляризации. Это может наблюдаться на сфере Пуанкаре (см. приложение 2), определяющей "покой" в связи со ссылкой, вызывающей вращение основных осей на темп вращения t_w (в рад/м). В этом сосотоянии покоя линейное двулучепреломление представлено стабильным экваториальным вектором , но есть дополнительный вектор кругового двулучепреломления 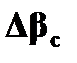, направленный дволь полярной оси, учитывающий изменение системы отсчета (Рисунок 7.2). Величина соотвествует t_w, но он соответствует противоположному направлению вращения. Общее двулучепреломление 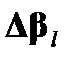получается просто как векторная сумма 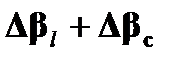. Величина 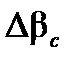гораздо меньше, чем , в противном случае поляризации вообще не будет сохранена; таким образом, два стабильных ортогональных состояния поляризации, слегка эллиптической, соответствуют пересечению 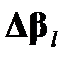со сферой Пуанкаре. Возвращаясь назад к "лабораторной" схеме двух состояний, сохраняющих ту же эллиптическую постоянную, но их мелкие и крупные оси вращаются относительно основных осей двулучепреломляющего волокна. Поляризация "медленно смещается" при повороте осей двулучепреломления и становится немного эллиптической.

 

Устойчивые эллипти-ческие состояния

Экватор

Полюс

Рисунок 7.2. Сфера Пуанкаре, описывающая стабильные эллиптические состояния поляризации в двулучепреляющих волокнах с вращением основной оси

В кольцевом интерферометре, используя такие сохраняющие поляризацию волокна, можно считать, что магнитное поле имеет незначительную зависимость от состояния поляризации в двух противоположных направлениях. Тем не менее, она модифицирует фазы противонаправленных волн в зависимости от коэффициента α _р, равного эллиптическому состоянию; то есть, соотношение 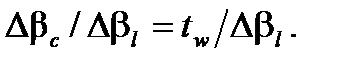Накопленная разность фаз Фарадея, поэтому

 

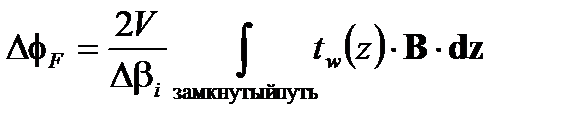(7.5)

 

В результате для круглой катушки радиусом R это дает

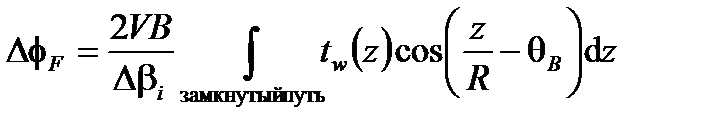(7.6)

 

где – угол вектора В с базовой осью. Эта формула эквивалентна "синхронной демодуляции" из степени изгиба t_w (z) как «частота» (2π R)^–1 из интегрального "времени" L.

Остаточная магнитная зависимость подходит, поэтому, от пространственных компонентов частоты t_w (z), равных обратному периметру 2π R в пределах ширины полосы пропускания, равной обратной общей длине катушки. Если предположить, что t_w (z) является случайной функцией с постоянной плотностью мощности, могут быть применены обычный результаты обнаружения белого шума, с применением усилителя.

Трудно оценить непосредственно эту плотность мощности, но это позволяет прогнозировать эффект увеличения длины известного волокна: он похож на процесс случайного блуждание и магнитная зависимость фазовой ошибки должна увеличиваться как увеличивается квадратный корень от длины (что эквивалентно времени интегрирования). С другой стороны, фазовая ошибка должна быть независимой от диаметра катушки и поворота периметра, если плотность мощности шума паразитарного кручения постоянна (т.е., частотно независима). Хороший порядок величины практической фазовой ошибки, вызванной магнитным полем Земли (т.е. 0,5G) –от 0,5 до 2 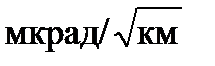(при λ=0,85 мкм), в зависимости от качества волокна. Поскольку чувствительность Саньяка пропорциональна длине и диаметру катушки, эквивалентные значения ошибки вращения за счет внешнего магнитного поля следует уменьшить пропорционально диаметру катушки и квадратному корню из ее длины.

Эта фазовая ошибка происходит от случайного процесса, паразитного уровня закручивания волокон высокого двулучепреломления; но для данной катушки гироскопа этот показатель является стабильным во времени, и магнитная зависимость не принесет долгосрочного дрейфа и шума, если гироскоп держит одинаковую ориентацию с магнитным полем. Гироскоп имеет оси и коэффициент магнитной чувствительности, которые являются стабильными и могут моделировать компенсацию предсказуемого смещения. Эта ось чувствительности находится примерно в плоскости катушки, поскольку эффект Фарадея является обнуляющий для магнитного поля, ортогонального в направлении распространения.

Если приложению требуется очень низкая магнитная зависимость, это позволяет получить дальнейшее совершенствование одного-двух порядков, измерительную катушку экранируют материалом с высокой магнитной проницаемостью, таким, как µ–метал. Обратите внимание на то, что, в связи с λ^–2 зависимостью эффекта Фарадея, использование больших длин волн (т.е. 1,3 или 1,55 мкм) снижает фазовую ошибку с коэффициентом 3-4, по сравнению с 0,85 мкм для аналогичных дефектов волокон.

Как мы уже видели, сохраняющие поляризацию волокна обеспечивают лучшее сокращение Фарадевской необратимости, чем обычные волокна. Вместе с тем было показано, что если расположить дополнительный деполяризатор между поляризатором и соединителем катушки в дополнение к деполяризатору катушки, необратимость Фарадея также значительно сокращается даже с катушкой из обычного волокна [8].

 

Нелинейный эффект Керра

Другой важный случай необратимого эффекта может возникнуть вследствие нелинейного оптического эффекта Керра [9]. Взаимности действительно основываются на линейном уравнении переноса (см. раздел 3.1), но дисбаланс в уровнях мощности противонаправленных волн может производить небольшие несогласованные разности фаз, в связи с распространением нелинейных, вызванных высокой оптической плотностью мощности в очень маленьком кремниевом ядре волокна. Медленные вариации в разделении коэффициента мощности делителя, возбуждение измерительной катушки может поэтому привести непосредственно к смещению дрейфа. Экспериментально разница мощности в 1 мкВт (например, вытекающая из 10^–3 дисбаланса разделения источника в 1мкВт) дает несогласованность с разностью коэффициентов менее, чем 10^–15; но при интегрировании вдоль нескольких сотен метров волокна это производит разность фаз в несколько 10^–5 рад, что по крайней мере на два порядка выше предела теоретической чувствительности. Она может быть сокращена, простым уменьшением мощности в волокне, но это приведет к увеличению влияния относительного шума детектирования.

В результате ошибки, индуцируемой эффектом Керра, вызванным скоростью вращения, на самом деле в результе сложного процесса смешивания четырех волн, и не просто самозависимая интенсивность распространения постоянной каждой противонаправлленной волны. Это также зависит от интенсивности противоположных волн [9, 10]. В линейной среде вектор электрической поляризации P определяется как (см. приложение I)

, (7.7)

 

но когда волна имеет высокую плотность энергии (т.е. большое Е поле), появляется дополнительный член нелинейной зависимости третьего порядка восприимчивость 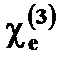и скаляр в квадрате | E |² электрического поля и P становится

(7.8)

Относительная диэлектрическая проницаемость 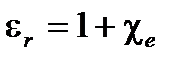меняется на

 

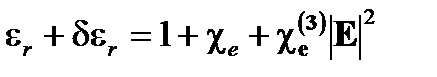(7.9)

 

и фактический показатель преломления 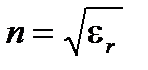имеет дополнительный нелинейный член

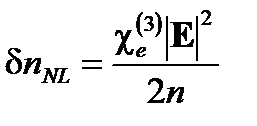. (7.10)

 

В кольцевом интерферометре, где два поля E₁ и E₂ распространяются в противоположных направлениях, два вектора поляризации P₁ и Р₂ должны быть рассмотрены в каждом направлении распространения. Бывшие взаимосвязи между векторами Р и Е применялись для одной волны, но теперь каждую противонаправленную волну нельзя считать независимой. Вектор общей поляризация Р₁ + P₂ относится к общему полю Е₁ + Е₂ и, следовательно,

 

. (7.11)

Потенциальный источник несогласованности вытекает из члена 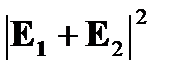, который представляет интенсивность постоянной волны, в результате интерференции между обоими противонаправленными полями Е₁ и Е₂.

При условии непрерывных монохроматических волн с одинаковым состоянием линейной поляризации и одинаковой частотой ω и постоянными противоположного направления распространения β и –β, имеем

 

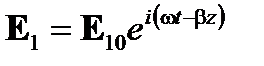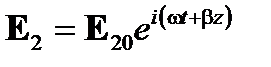, , (7.12)

 

где z – пространственная продольная координата вдоль волокон катушки. После 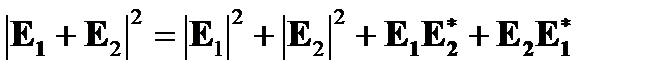это дает

 

(7.1З)

 

Первые два условия этого отношения зависят от суммы квадратов полей (т.е. интенсивностей) двух волн и поэтому дают нелинейные коэффициенты изменения для Е₁ и Е₂ в каждом противоположном направлении. С другой стороны два последних члена индуцируют несогласованность, поскольку

 

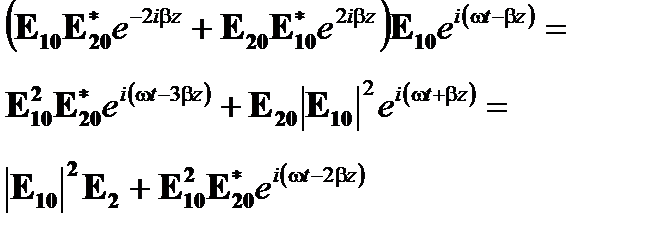(7.14)

и точно так же,

 

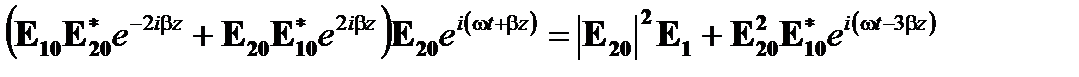. (7.15)

 

Влияние членов при пространственной частоте 3β или –3β дает среднюю величину в распространении, но два других члена β и –β соответствущих фаз дают постоянное изменение чувствительности при распространении волн. Каждый вектор поляризации является на самом деле

 

(7.16)

 

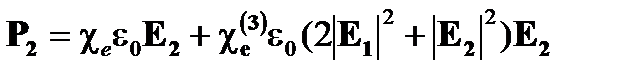
Это дает различные нелинейные изменения показателя преломления для каждого противоположного направления:

 

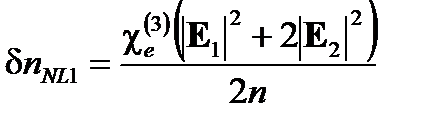
(7.17)

 

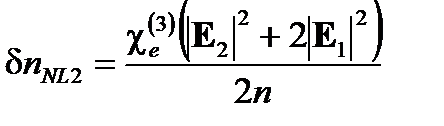
и разность несогласованного показателя преломления:

 

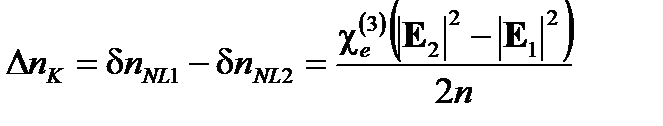(7.18)

 

Исходя из единой интенсивности распределения в области ядра диаметром около 5 мкм, эта индуцируемая эффектом Керра разность может быть оценена значением 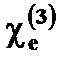в кремнии в зависимости от разности мощности Δ P (пропорциональной 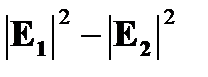) между обоими направлениями, как [9]:

 

.

 

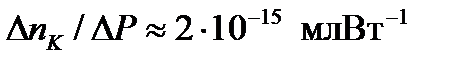Эта разница очень мала, но для эффекта Саньяка при интегрировании по всей длине L волокна катушки дает значительный рост разности фаз 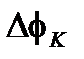. На длине волны от 0,633 мкм [9]:

 

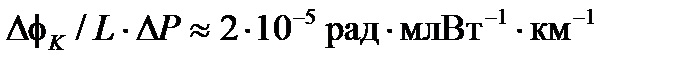(7.19)

 

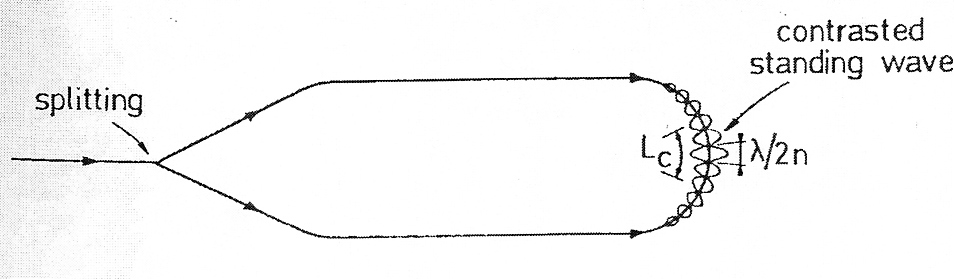
Этот анализ показывает, что результаты несогласованности эффекта Керра следуют исключительно из-за образования нелинейного показателя дифракционной решетки, из-за интерференции между двумя противонаправленными волнами внутри волокон, которую дает постоянная волна. Как установлено раннее в [10], если различие этой постоянной волны вымывается в некоторых процессах, несогласованность следует уменьшить. Этот важный момент объясняет, почему использование широкополосных источников с короткой длиной когеренции значительно снижает несогласованность Керра: постоянная волна сопоставима только на расстоянии, равном длине когерентности L_c в середине волоконной катушки (Рисунок 7.3), и поэтому эффект несогласованной разности показателя преломления интегрирован только вдоль L_c, а не вдоль всего волокна длиной L!

 

Разделение

Рисунок 7.3. Сопоставление стоячих волн в средней части волоконной катушки

Сопоставление стоячих волн

 

Отмена несогласованности Керра с широкополосным источником первоначально объяснили статистикой колебаний интенсивности света [11,12]. Фактически это оригинальное объяснение рассматривает случай интенсивности модулированной волны, который дает нелинейные возмущения показателя преломления, зависящие от времени t и координаты z в волокне:

 

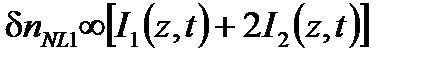
(7.20)

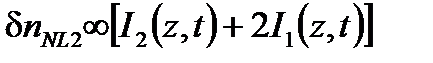
Важной особенностью этих уравнений, как мы уже видели, является эффект пересечения мощности одной волны дважды, ее самоэффект. Использование в прямоугольной модуляции интенсивности волны монохроматического источника впервые предложено для снижения несогласованности Керра в работе [13]. В этом случае скрещенные эффекты присутствуют только тогда, когда обе противонаправленные интенсивности совпадают (Рисунок 7.4) (т.е. половину времени), в то время как самоэффект представлен все время. Таким образом, второй фактор эффекта пересечения уменьшает усредненное значение единства, которое эффективно отменяет несогласованность, так как осцилляции средней фазы становятся идентичными в обоих направлениях.

Рисунок 7.4. Прямоугольно модулированные противоположно направленные волны интенсивности для снижения несогласованности из-за эффекта Керра

Такого рода компенсации не ограничиваются прямоугольными волнами, и это применяется, если среднее значение < I > модулируемой интенсивности равно его стандартному отклонению 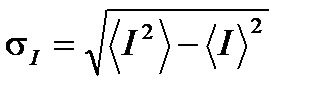[11,12]. Благодаря центральной предельной теореме, поляризация широкополосного источника имеет случайные интенсивности с экспоненциальной вероятностью распределения:

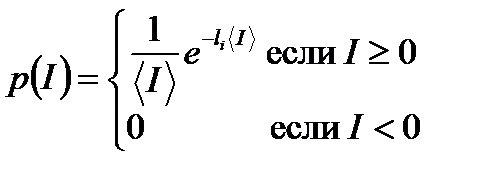(7.21)

 

и это выполняет требование 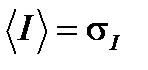, которое обеспечивает отсутствие несогласованности, вызванной эффектом Керра.

 

Это последнее объяснение, однако, вводит в заблуждение, создавая ощущение, что уменьшение эффекта несогласованности Керра связано с источником широкополосной связи, что "происходит", чтобы иметь адекватную статистику, с которой очень "повезло". С другой стороны, непосредственный анализ нелинейного процесса ясно показывает, что это связан с феноменом интерференции стоячей волны, и что низкокогерентный источник уменьшает паразитные эффекты таким же образом, уже очень выгодно с обратным рассеянием и отражением или несогласованной поляризацией, которые также зависят от феномена паразитной интерференции.

Однако сходство в членах когеренции между нелинейным эффектом и других когерентно связанных линейных эффектов ограничено использованием широкополосных источников с непрерывным распространением света, что разрушает контраст стоячих волн, но гарантирует, что обе противонаправленные интенсивности света являются постоянными в волокне. Очень короткие импульсы также могут ограничивать эффект когерентного обратного отражения, обратного рассеяния и несогласованности поляризации, но для проблемы нелинейности каждого противонаправленного импульса будет испытываться главным образом самоэффект, который даст несогласованность с дисбалансом мощности. Кроме того для одной средней мощности нелинейность далее увеличится, поскольку это зависит от пика мощности, которые намного выше в случае возникновения пульсации.

Обратите внимание, что было бы интересно изучить эффект дополнительной фазовой модуляции, особенно в средней части петли, чтобы увидеть, если это также возможно, это означает, что уменьшить контрастность стоячих волн и установить связь несогласованного Керра, несмотря на источник высокой когерентности.

Ссылки

[1] Arditty, д. х., ю. Bourbin, м. Papuchon и C. Puech, "Датчик тока с использованием самой современной волоконно-оптической интерферометрической техники," Proceedings of ИООК, документ WL3, 1981.

[2] Бома, К., К. Petermann и е. Weidel, "Чувствительность волоконного гироскопа к окружающим магнитным полям" оптика письма, том 7, 1982, pp. 180-182 (MS SPIE 8, стр. 328-330).

[3] Шиффнер, г., б. Nottbeck и г. Schroner, "Волоконно-оптический датчик вращения: анализ эффектов ограничения чувствительности и точности" Springer серии в оптический наук, Vol. 32, 1982 г., стр. 266-274.

[4] Берг, р. а., г. С Лефевр и H. J. шоу, "Многомодовый волоконно-оптический гироскоп" Springer серии в оптический наук, Vol. 32, 1982 г., стр. 252-255.

[5] Берг, р. а., г. С Лефевр и H. J. шоу, "Геометрическая волоконная конфигурация для изоляторов и магнитометров," Springer серии в оптический наук, Vol. 32, 1982, pp. 400-405.

[6] Хотате, K. и K. Tabe, "Дрейф оптического волоконного гироскопа, причиненный эффектом Фарадея: влияние магнитного поля Земли" прикладной оптики, Vol. 25, 1986, pp. 1086-1092 (MS SPIE 8, стр. 331-337).

[7] Марроне, я. м., C. а. Villaruel, н. д. Фриго и а. Dandridge, "Внутреннее вращение осей двулучепреломления в сохраняющих поляризацию волокнах" оптика письма, том 12, 1987, pp. 60-62.

[8] Блейк, J., "Чувствительность к магнитному полю деполяризованного волоконно-оптического гироскопа" SPIE труды, том 1367, 1990, pp. 81-86.

[9] Иезекииль, S., д. л. Дэвисом и р. в. Hellwartli, "Интенсивность зависящего несогласованного сдвига фаз в волоконно-оптическом гироскопе" Springer серии в оптический наук, Vol. 32, 1982, pp. 332-336 (MS SPIE 8, стр. 308-312).

[10] Каплан, а. и. п. Meystre, "Большое повышение эффекта Саньяка в нелинейном кольцевом резонаторе и смежные эффекты" Springer серии в оптический наук, Vol. 32, 1982, pp. 375-385.

[11] Берг, р. а., б. Culshaw, С. С. Катлер, H С Лефевр и H. J. шоу, "Источник статистик и эффект Керра в волоконно-оптических гироскопах" оптика письма, том 7, 1982, pp. 563-565 (MS SPIE 8, стр. 313-315).

[12] Petermann, K., "Зависящий от интенсивности несогласованный сдвиг фаз в волоконно-оптических гироскопах для источников света с низким уровнем когерентности" оптика письма, том 7, 1982, pp. 623-625 (MS SPIE 8, стр. 322-323).

[13] Берг, р. а., г. С Лефевр и H. J. шоу, "Компенсация оптического эффекта Керра в волоконно-оптических гироскопах," письма оптики. Индекс vol.7, 1982, pp. 282-284 (MS SPIE 8, pp. 316-318).

 

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: