 |
Задача 5 Системы одновременных уравнений.
|
|
|
|
1. Оценить следующую структурную модель на идентификацию:
 ,
,
 ,
,
 .
.
2. Исходя из приведенной формы модели уравнений
 ,
,
 ,
,
 ,
,
найти структурные коэффициенты модели.
Решение:
1. Модель имеет три эндогенные (y1, y2, y3) и три экзогенные (x1, x2, x3) переменные.
Проверим каждое уравнение системы на необходимые (H) и достаточное (Д) условия идентификации.
Первое уравнение:
Н: эндогенных переменных – 2 (y1, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют y2 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y2 | x2 | |
| Второе | -1 | a22 |
| Третье | b32 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение:
Н: эндогенных переменных – 3 (y1, y2, y3),
отсутствующих экзогенных – 2 (x1, x3).
Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| x1 | x3 | |
| Первое | a11 | a13 |
| Третье | a31 | a33 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Третье уравнение:
Н: эндогенных переменных – 2 (y2, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
|
|
|
| Уравнение | Отсутствующие переменные | |
| y1 | x2 | |
| Первое | -1 | 0 |
| Второе | B21 | a22 |
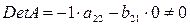 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Вычислим структурные коэффициенты модели:
1) из третьего уравнения приведенной формы выразим x2 (так как его нет в первом уравнении структурной формы):
 .
.
Данное выражение содержит переменные y3, x1 и x3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x2 в первое уравнение приведенной формы модели (ПФМ):
 Þ
Þ 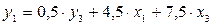 – первое уравнение СФМ;
– первое уравнение СФМ;
2) во втором уравнении СФМ нет переменных x1 и x3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим x1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
 .
.
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ.
Выразим x3 из третьего уравнения ПФМ:
 .
.
Подставим его в выражение x1:
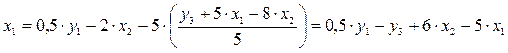 ;
;
 .
.
Второй этап: аналогично, чтобы выразить x3 через искомые y1, y3 и x2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ:
 .
.
Следовательно, 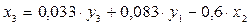 .
.
Подставим полученные x1 и x3 во второе уравнение ПФМ:
 Þ
Þ
 – второе уравнение СФМ.
– второе уравнение СФМ.
Это уравнение можно получить из ПФМ иным путем. Суммируя все уравнения, получим
 ,
,
 ,
,


Далее из первого и второго уравнений ПФМ исключим x1, домножив первое уравнение на 3, а второе – на (-2) и просуммировав их:
 ,
,


Затем аналогичным путем из полученных уравнений исключаем x3, а именно:
 ½-26,
½-26,
 ½ 17,
½ 17,
 ,
,
 , Þ
, Þ

 Þ
Þ  ;
;
|
|
|
3) из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:  .
.
Подставим полученное выражение в третье уравнение ПФМ:
 Þ
Þ  – третье уравнение СФМ.
– третье уравнение СФМ.
Таким образом, СФМ примет вид:
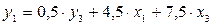 ,
,
 ,
,
 .
.
Задача 5. Имеются структурная модель и приведенная форма модели. Используя таблицу соответствующего варианта:
- оценить данную структурную модель на идентификацию;
- исходя из приведенной формы модели уравнений найти структурные коэффициенты модели.
Вариант 1. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
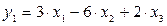 ,
,
 ,
,
 .
.
Вариант 2. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
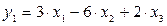 ,
,
 ,
,
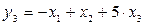 .
.
Вариант 3. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
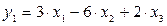 ,
,
 ,
,
 .
.
Вариант 4. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
 ,
,
 ,
,
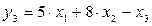 .
.
Вариант5. Структурная модель:
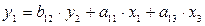 ,
,
 ,
,
 .
.
Приведенная форма:
 ,
,
 ,
,
 .
.
Вариант 6. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
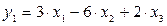 ,
,
 ,
,
 .
.
Вариант 7. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
 ,
,
 ,
,
 .
.
Вариант 8. Структурная модель:
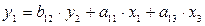 ,
,
 ,
,
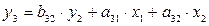 .
.
Приведенная форма:
 ,
,
 ,
,
 .
.
Вариант 9. Структурная модель:
 ,
,
 ,
,
 .
.
Приведенная форма:
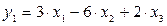 ,
,
 ,
,
 .
.
Вариант 10. Структурная модель:
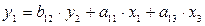 ,
,
 ,
,
 . Приведенная форма:
. Приведенная форма:
 ,
,
 ,
,
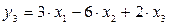 .
.
|
|
|


