 |
Схема ЦАП с суммированием напряжений
|
|
|
|
Одна из таких схем с суммированием напряжений на операционном усилителе приведена на рисунке 10.1.
Триггеры 1…n образуют регистр, в который помещаются двоичные числа, предназначенные для перевода в пропорциональные им значения напряжения на выходе. Будем считать, что напряжение на выходе каждого из триггеров может принимать одно из двух возможных значений: Е при состоянии 1 и 0 при состоянии 0.
Рисунок 10.1
Напряжение с выходов триггеров передаются на выход ЦАП через операционный усилитель (ОУ), работающий в режиме взвешенного суммирования напряжений (аналогового сумматора) для каждого триггера предусматривается, отдельны вход в сумматоре с коэффициентом
Таким образом, напряжение с выхода триггера n-го разряда передаётся на выход усилителя с коэффициентом передачи:
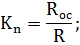
этот коэффициент для (n - 1) - го разряда 
для (n - 2) - го разряда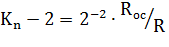 
и т.д.
Обратим внимание на то, что коэффициенты передачи усилителя с отдельных его входов находится в том же соотношении, что и весовые коэффициенты соответствующих разрядов двоичного числа. Так, Kn в два раза больше Kn-1 и весовой коэффициент n-го разряда в два раза больше весового коэффициента (n–1) - го разряда. Следовательно, напряжение, передаваемые на выход усилителя с выходов триггеров отдельных разрядов, находящихся в состоянии 1, пропорциональны весовым коэффициентам разрядов.
Если в состоянии 1 находится одновременно триггеры нескольких разрядов, то напряжение на выходе усилителя равно сумме напряжений, передаваемых на этот выход от отдельных разрядов двоичного числа в регистре: an, an-1,…,a1. Тогда напряжение на выходе усилителя
Здесь N – десятичное значение двоичного числа, введённого в регистр.
|
|
|
Из последнего выражения видно, что напряжение на выходе ЦАП пропорционально числу в регистре.
Недостатки рассмотренной схемы преобразователя:
· используется высокоточные резисторы с различными значениями сопротивления;
· трудно обеспечить высокую точность выходного напряжения триггеров.
Указанные недостатки устранены в схеме ЦАП с суммированием напряжений на резисторной матрице R и 2R, приведённой на рисунке 10.2.
Рисунок 10.2
На рисунке 10.2 представлена схема трёхразрядного преобразователя. Особенности схемы с суммированием напряжений на резисторной матрице R и 2R состоит в том, что, во-первых, используются резисторы лишь с двумя значениями сопротивления (R и 2R) и, во-вторых, выходные напряжения триггеров непосредственно не участвуют в формировании выходного напряжения ЦАП, а используется лишь для управления состоянием ключей.
В каждом разряде ЦАП имеется два ключа, через один из них в резисторную матрицу подаётся напряжение E, через другой – нулевое напряжение.
Ключи преобразователя с суммированием напряжения на резисторной матрице выполнены по схеме, представленной на рисунке 10.3.
Рисунок 10.3
Транзисторы VT1 и VT2 управляются напряжениями с выходов триггера. Выход схемы подключается к резисторной матрице.
Пусть триггер находится в состоянии 1. На его инверсном выходе низкий потенциал и транзистор VT2, на базу которого поступает этот потенциал, закрыт.
На прямом выходе триггера Тесятичное двоичного числа, введённого в регистр. от отдельных разрядов двоичного числа разрядов. напряжение высокого уровня. Оно поступает на вход транзистора VT1 и удерживает его в открытом состоянии. Через открытый транзистор VT1 в резисторную матрицу подаётся напряжение, близкое к Е.
Если триггер находится в состоянии 0, закрыт транзистор VT1, а через открытый транзистор VT2 в резисторную матрицу поступает напряжении низкого уровня.
|
|
|
Таким образом, реализованная по данной схеме устройство выполняет роль двух ключей в разряде преобразователя.
Определим напряжение на выходе ЦАП, соответствующий единицам разрядов числа, помещаемого в регистр.
Пусть в регистр введено число 1002. Триггер 3 в состояние 1, и в третьем разряде открыт ключ (Кл3), в остальных разрядах триггеры в состоянии 0 и открыты ключи 2’ и 1’ (рисунок 10.4,а).
Рисунок 10.4
Последовательными преобразованиями можно получить схему (рисунок 10.3, д), из которой следует, что напряжение в точке А3 равно 
Если в регистр поместить число 0102, то резисторную матрицу можно представить схемой, показанной на рисунке 10.5.
Рисунок 10.5
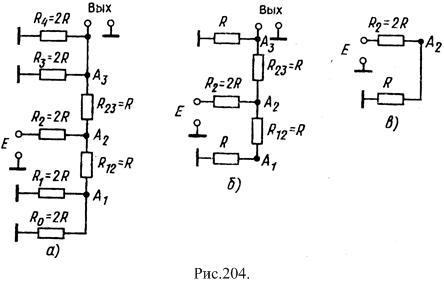
Путем преобразования её можно привести к схеме, представленной на рисунке 10.4,в. Возникающие в точке А2 напряжение имеет тоже значение, что и в точке А3 схемы на рисунка 10.4. Из рисунка 10.5, а видно, что при передаче на выход преобразователя это напряжение делится на два и, таким образом,
Можно показать, что при числе 0012 напряжение в точке А1 = UA1 = E / 3. При передаче этого напряжения в точку А2 и далее от точки А2 к точке А3 напряжение каждый раз делится на два и 
Итак, напряжение на выходе соответствующее единицам отдельных разрядов двоичного числа в регистре, пропорционально весовым коэффициентам разрядов.
При n-разрядном регистре, обозначив цифры разрядов двоичного числа аn,аn-1,…,а1, получим выражение напряжения на выходе ЦАП:
Из выражения видно, что выходное напряжение ЦАП пропорционально числу N, помещаемому в регистр.
Аппаратурные погрешности преобразования данной схеме связаны с отклонениями сопротивления резисторов от их номинальных значений, не идеальностью ключей (сопротивление реального ключа в закрытом состоянии не равно бесконечности, а в открытом – не равно 0), нестабильностью источника напряжения Е. Наибольшее влияние на погрешность ЦАП оказывают эти отклонения в старших разрядах.
|
|
|
