Понятие средней ошибки выборки

Математическая теория выборочного метода имеет своей целью формулировку точных критериев выборочного исследо­вания. Эти критерии призваны оптимизировать процессы отбо­ра, обследуемых единиц из генеральной совокупности, обеспе­чить получение представительной выборки и определить ее наилучший объем. Методы математической статистики в дан­ном случае призваны дать ответ на два основных вопроса: ка­кова надежность результатов выборочного исследования и ка­ков необходимый объем выборки.

Отклонение статистической структуры выборки от "ис­тинной" структуры генеральной совокупности называют ошиб­кой выборки (или ошибкой репрезентативности).*

* Репрезентативность — это свойство выборки воспроизводить характе­ристики генеральной совокупности. Следует особо подчеркнуть, что ма­тематическая статистика имеет дело только со случайными ошибками выборки. Другие виды ошибок репрезентативности (например, ошибки регистрации и т. д.) лежат за пределами этой науки.

 

Ошибка выборки в общем виде может быть представлена так:

где D — ошибка выборки;

P_B — исследуемый показатель в выборочной совокупности; Р_Г — исследуемый показатель в генеральной совокупности. На практике часто используется понятие средней ошиб­ки выборки.

В качестве примера возьмем изучение правовой культу­ры. В результате применения выборочного метода установле­но, что в среднем в домашней библиотеке каждой семьи име­ется 6,5 экземпляров юридической литературы.

В действительности же число таких изданий составило 7,1 единицы.

Средняя ошибка выборки в этом случае составит:

D = 7,1 - 6,5 = 0,6.

Ошибку репрезентативности чаще всего характеризуют процентным отношением ошибки к соответствующей средней. В нашем примере эта ошибка равна:

D = 0,6 / 6,5 • 100 = 9%.

Определение объема выборки

Для определения необходимой численности выборки сле­дует задать уровень точности выборочной совокупности с оп­ределенной вероятностью. В частности, объем выборочной со­вокупности в простой вероятностной выборке определяется по формуле:

которая следует из формулы предельной ошибки выборки:

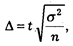
где п — объемвыборочной совокупности,

s² — дисперсия изучаемого параметра в генеральной со­вокупности,*

t — коэффициент доверия — показатель, который харак­теризует вероятность реализации той или иной выборки,

D — предельная ошибка выборки.

* Дисперсия — величина, которая характеризует меру однородности ге­неральной совокупности. Чем дисперсия больше, тем меньше мера одно­родности генеральной совокупности. Чем дисперсия меньше, тем одно­родность генеральной совокупности больше.

 

Предельная ошибка содержит информацию о точности выборки с определенной вероятностью.

Вероятность задается коэффициентом доверия. В эту фор­мулу не входит объем генеральной совокупности (N), что не случайно. В математической статистике установлено, что для выборок из большой генеральной совокупности объем исходно­го материала не оказывает влияния на объем выборочной со­вокупности (те).

Как правило, объем генеральной совокупности в правовых исследованиях очень большой, поэтому нет оснований опреде­лять объем выборки в долях. Определение необходимого объе­ма выборки часто составляет серьезную проблему. Это связа­но, в частности, с неразработанностью ряда вопросов (оценка вариации изучаемых признаков, обоснование численности вы­борки при изучении нескольких признаков и др.).

Виды выборки

В правовых исследованиях применяются следующие виды выборки:*

простая вероятностная (или собственно случайная) выборка,

систематическая вероятностная,

типическая выборка,

многоступенчатая выборка,

квотная выборка.

* Различные авторы при классификации видов выборок применяют различ­ную терминологию, но суть этих классификаций остается одной и той же.

 

Простая вероятностная (собственно случайная) выбор­ка применяется в тех случаях, когда объем генеральной сово­купности относительно невелик и есть возможность доступа к каждому элементу. В этом случае каждый элемент генераль­ной совокупности имеет равные шансы попасть в выборочную совокупность.

Объектов, которые наиболее часто встречаются в гене­ральной совокупности, будет больше и в выборке, и наоборот.

Отбор элементов в выборочную совокупность чаще всего производится методом жеребьевки или по таблице случайных чисел.

При отборе с помощью жеребьевки следят за тем, чтобы количество жребиев соответствовало объему генеральной со­вокупности. Каждый из элементов жеребьевки (шары, карточ­ки, фишки) должен содержать информацию об отдельной еди­нице совокупности (номер, название или какой-либо другой отличительный признак).

Количество жребиев, установленное в соответствии с оп­ределенным процентом отбора, извлекается из общей их сово­купности в случайном порядке. При использовании для отбора таблиц случайных чисел каждая единица генеральной сово­купности должна иметь порядковый номер.*

* Таблицы случайных чисел представляют собой абсолютно произвольные столбцы цифр, полученные с помощью датчика случайных чисел на ЭВМ.

 

Систематическая вероятностная выборка используется в тех случаях, когда генеральная совокупность носит упорядо­ченный характер, например списки гражданских дел; число работников государственного органа; список депутатов зако­нодательного (представительного) органа; список мер наказа­ний, назначенных определенной группе осужденных; список хозяйствующих субъектов на территории района и др.

При организации систематической выборки устанавлива­ется пропорция отбора путем соотношения выборочной и гене­ральной совокупностей. В качестве примера возьмем генераль­ную совокупность в 10 тыс. уголовных дел осужденных за умыш­ленное убийство и 5% выборку. Пропорция отбора составит:

Отбор единиц осуществляется в соответствии с установ­ленной пропорцией через равные интервалы. В данном случае отбирается каждое 20-е уголовное дело.

Средняя ошибка систематической выборки рассчитывается по формуле для простой вероятностной выборки. Так, при изу­чении личности повторных правонарушителей в двух индустри­ально-аграрных районах РФ применялась простая вероятностная выборка. Из общего массива статистических карточек была получена выборочная совокупность объемом в 4 тыс. единиц.

Для обеспечения такого отбора была получена последова­тельность случайных чисел, т. е. чисел, в чередовании кото­рых нет никакой закономерности. Эта последовательность стро­илась с применением специальной программы на ЭВМ БЭСМ-ЗМ. Затем полученные числа были упорядочены по возраста­нию, т. е. ранжированы по величине. Для уточнения выборки были сформированы группы объемом соответственно 500, 1000, 1500, 2000, 3000 и 4000 карточек, образованные по принципу случайного отбора.

Воспользуемся данным примером и выполним некоторые расчеты. Вычислим максимальную ошибку выборки.*

* Максимальной ошибкой выборки называется величина наибольшего от­клонения генеральной средней от выборочной, которая может иметь ме­сто с заданной доверительной вероятностью.

 

С этой целью возьмем формулу предельной ошибки для простой вероятностной выборки:

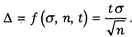
Обычно коэффициенту доверия t придают значения 1, 2, 3. При t = 1 вероятность, P(t) отклонения выборочных характери­стик от генеральных средних на величину одного среднеквад­ратичного отклонения равна 0,683.

При вычислении объема выборки в нашем примере вос­пользуемся следующими значениями параметров, входящих в формулу объема выборки:

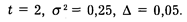
Подставим эти значения в нашу формулу и выполним вы­числения:

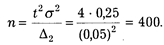
Мы видим, что необходимый объем выборки при задан­ных условиях является относительно небольшим.

В нашем примере объем выборки равен 4000 карточек — с учетом того, что достаточным должен быть объем и для таких показателей, которые имеют весьма небольшой удельный вес во всей генеральной совокупности.*

* В математической статистике разработана теория так называемых "ма­лых выборок" (В. Госсет, Р. Фишер, А, Колмогоров). Согласно этой тео­рии при выполнении определенных условий выборка может быть доста­точно представительной при объеме в 20 наблюдаемых единиц.

 

Таким образом, из этой формулы видно, что для увели­чения точности выборочной совокупности необходимо соблю­дение двух требований:

1) изучаемый признак в генеральной совокупности должен быть как можно более однородным;

2) объем выборочной совокупности должен быть как мож­но большим.

В правовых исследованиях простая вероятностная выбор­ка имеет ограниченное применение, что связано со сложной иерархической структурой изучаемых социальных объектов.

Это заставляет использовать комбинированные выборки, сочетающие элементы различных приемов.

Типическая выборка применяется в том случае, когда ге­неральная совокупность неоднородна с точки зрения социаль­но-демографических, экономических или иных признаков. При­чем все единицы генеральной совокупности можно разбить на несколько типических групп. Типический отбор предполагает выборку единиц из каждой группы с использованием простой или систематической вероятностной выборки.

Отбор единиц в такую выборку может производиться про­порционально либо объему типических групп, либо внутригрупповой дифференциации признака.

Например, при изучении личности преступника всю сово­купность осужденных обычно разбивают по возрастам, выде­лив такие группы, как несовершеннолетние, осужденные сред­него и старшего возраста. Образованные подобным образом группы неравны между собой. Поэтому отбор выполняется про­порционально объему групп.

При данном отборе в выборку попадают представители всех типических групп. Вследствие этого достигается большая точ­ность выборки.

Необходимость применения многоступенчатой выборки вызвана, как правило, отсутствием информации обо всех еди­ницах наблюдения генеральной совокупности.

Для организации первой ступени достаточно иметь инфор­мацию о распределении признака отбора. Для проведения от­бора во второй ступени используется информация об отобран­ных единицах первой ступени.

Таким образом, на каждой ступени меняется единица от­бора. На первой ступени обычно используется строго случай­ный, а на последующих (начиная со второй) — вероятностный пропорциональный отбор, т. е. учитывается размер единиц первой ступени, попавших в выборку.

Доли отбора на каждой ступени комбинируются таким об­разом, чтобы всем единицам генеральной совокупности были обеспечены равные шансы попасть в выборку.

В правовых исследованиях наиболее часто используется производственно-территориальная выборка: на первых ступе­нях отбора в качестве гнезд выступают регионы (области, го­рода, районы и т. д.), а на последних — производственные единицы (предприятия, заводы, цехи, бригады и т. д.).

Как видим, многоступенчатый отбор по своей природе является гнездовым. Под гнездом понимается тот промежуточ­ный объект исследования, который отбирается на каждой сту­пени для того, чтобы служить исходной совокупностью для последующего отбора.

При многоступенчатом отборе (начиная с двухступенча­той выборки) необходимо учитывать специфику расчета ошибки репрезентативности. Каждая ступень отбора вносит свои от­клонения в истинные параметры генеральной совокупности. Рас­чет ошибок многоступенчатой выборки связан с большими труд­ностями.

Для достаточно объемной выборки существуют упрощен­ные формулы расчета ошибки репрезентативности. Упроще­ние состоит в том, что в математической статистике принято производить расчеты внутригрупповых дисперсий первой сту­пени отбора после того, как из нее отобраны единицы второй ступени.

Ошибка двухступенчатой выборки исчисляется по фор­муле:

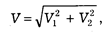
где V₁ — ошибка первой ступени, V₂ — ошибка второй ступени.

Двухступенчатый отбор был применен в ходе изучения уровня юридических знаний и источников правовой информа­ции населения Ленинграда.*

* Работа проводилась в Научно-исследовательском институте комплекс­ных социальных исследований в 80-х годах.

 

За основу выборочного исследования были приняты спис­ки жителей в домовых книгах.

Исследователи исходили из предположения, что населе­ние города распределяется по районам в относительно слу­чайном порядке. Домовые хозяйства города отбирались в со­ответствии с таблицами случайных чисел. Из полученных в результате списков отбирался каждый девятый человек. Ко­нечный объем выборки был определен в 3 тыс. человек с уче­том того, чтобы в ней были представлены различные группы лиц по социальному положению, полу, возрасту, образова­нию.

Многоступенчатый отбор использовался при изучении правосознания граждан.*

* В работе принимали участие сотрудники Института государства и пра­ва РАН совместно с ВНИИ советского законодательства.

 

Классические выборочные схемы сформировались под оп­ределяющим влиянием запросов экономической и технической практики. Специфика выборочного исследования правовых объек­тов отражена в этих методах в недостаточной мере. В условиях интенсивного развития социологических исследований возни­кает потребность в разработке новых приемов и новых матема­тических средств получения выборочных совокупностей.

Совокупность социально-экономических и демографичес­ких признаков, детерминирующих исследуемый правовой по­казатель, должна находиться в выборке в тех же соотношени­ях, в тех же пропорциях и связях, что ив генеральной сово­купности. Достичь такого формирования выборки можно раз­личными путями. При чисто случайном отборе пропорции детермирующих факторов осуществляются автоматически. Од­нако можно пойти другим путем и отбирать из состава гене­ральной совокупности такие единицы, которые обладают за­данными признаками, и затем из них формировать выбороч­ную совокупность. В этом случае речь идет о методе квот ("квотной выборке").

Для применения метода квот необходимо привлекать об­ширную статистическую информацию, характеризующую генеральную совокупность. При этом составляются так называе­мые расчетные таблицы населения по полу, возрасту, обра­зованию и другим признакам. Таблицы показывают, в какой именно пропорции должны быть отобраны единицы выбороч­ного наблюдения.

Метод квот не позволяет использовать аппарат матема­тической статистики, рассчитанный на случайный отбор. Вместе с тем в практике конкретных правовых исследований сформировалось положительное отношение к использованию этого метода как одного из способов отбора единиц наблю­дения.

Заключительным этапом выборочного наблюдения явля­ется распространение его результатов на генеральную сово­купность. При этом необходимо учитывать полноту выборки, т. е. наличие в ней всех типов или групп данной генеральной совокупности. Заметим, что неполнота выборки может приве­сти к нарушению репрезентативности, а стало быть, и к не­правильным выводам. В этих случаях прибегают к корректи­ровке выборки.

§ 3. Методы изучения взаимосвязей социально-правовых явлений

Известно, что в явлениях природы существует всеобщая связь. Такая связь наблюдается и в общественных явлениях, включая государство и право. Одна из важных задач правовых конкретно-социологических исследований состоит в изучении причинных и обусловливающих связей. Особая роль здесь при­надлежит многофакторному анализу — комплексному иссле­дованию воздействия различных экономических, политичес­ких, социальных и иных факторов на социальную обусловлен­ность правовых норм, действенность правовой пропаганды, правового воспитания и т. д.

Математика различает функциональные и статистические связи между величинами. Функциональными называют одно­значные связи между двумя и более величинами. В основе математического понятия функциональной связи лежит фун­даментальное понятие функции как однозначного соответствия между элементами различных множеств. Функциональные свя­зи более распространены в области естественных и техничес­ких наук и только отчасти — в общественных науках.

В отличие от функциональной статистическая связь меж­ду величинами представляет собой связь неоднозначную, ве­роятностную, "размытую" действием различных побочных для данного процесса факторов (так называемых случайных свя­зей). При статистической связи вполне определенному значе­нию одной переменной соответствует одновременно несколько значений другой переменной. Результативный признак реаги­рует на изменения факторного признака статистическим рас­пределением своих показателей. Эти связи более распростра­нены в общественных науках. Так, для взятого наугад индиви­да набор параметров, характеризующих его правовые ориен­тации, знание правовых норм и т. д., не будет однозначно определенным. Данный набор значительно варьирует в преде­лах группы индивидов с заранее взятыми социально-демогра­фическими характеристиками. Аналогичным образом можно констатировать статистическую связь между возрастом инди­видов и степенью приобщенности их к деятельности средств массовой информации и т. д.

Статистическая связь существует между тяжестью совер­шенного преступления и назначенным наказанием. Фактора­ми, которые делают подобного рода связь статистической, являются: личность осужденного, реальная тяжесть содеянно­го, условия вынесения приговора по данному делу, учет смяг­чающих и отягчающих обстоятельств и т. д.

При этом необходимо различать качественные и количе­ственные признаки.

Качественный признак характеризует наличие или отсут­ствие какого-либо свойства у единиц наблюдения. Например, качественными признаками являются пол, место жительства, семейное положение, социальный статус гражданина. К их чис­лу относится юридическая квалификация действий субъекта по какой-либо статье нормативного акта. В этих случаях нет возможности установить количественный характер исследуе­мых данных применительно к каждому изучаемому объекту. Он устанавливается только при обсчете единиц всей совокуп­ности.

Примерами количественных признаков могут служить: размер наказания в годах лишения свободы, численность ап­парата управления, численность населения, размер террито­рии.

Математические методы и ЭВМ нужны главным образом для того, чтобы изучать социальные явления во взаимосвязи.

Речь идет, например, о разработке таких алгоритмов и про­грамм, которые дали бы возможность изучать количественно меру влияния различных экономических, демографических и иных факторов на государственно-правовые явления. Следо­вательно, основная задача при разработке программы машин­ной обработки юридических данных — это автоматизация на­учного статистического анализа (синтеза) в области права.

В основе многих правовых конкретно-социологических исследований лежит упорядочение исходных данных путем различных статистических группировок. Эти группировки раз­нообразны: простые, вторичные, аналитические, комбинаци­онные.

Для широкого практического применения в программу ЭВМ следует включить такой относительно простой метод об­работки информации и установления связи между параметра­ми, входящими в предмет исследования проблемы, как метод комбинационных статистических группировок. В этих груп­пировках единицы, образованные сначала по одному призна­ку, делятся затем на подгруппы по значениям другого при­знака, т. е. дается "разрез" признаков по различным комбина­циям.

В случае многозначности признака исследуемая совокуп­ность может быть разделена на n частей (A ₁, А ₂,... A_n по признаку А, и затем каждая из полученных групп делится по второму признаку В на т частей: B ₁, B ₂ ,..., В_m. Итого имеем пт заключающих численностей.

Примером комбинационной таблицы может служить кор­реляция между образованием и предпочтением источника мас­совой информации о праве (см. табл. 1).

Таблица 1. Образование и предпочтение источника массовой информации о праве*

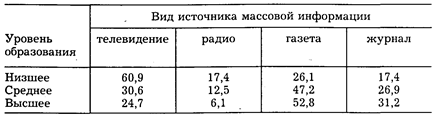
* Сумма процентов на строке превышает 100, так как некоторые респон­денты называли одновременно несколько источников.

 

Метод комбинационных статистических таблиц в некото­рых случаях может содержать более полезную информацию, чем коэффициенты связи. При вычислении коэффициентов свя­зи происходит некоторая потеря информации. Так, в строках таблицы могут содержаться весьма характерные распределе­ния статистических показателей, которые нивелируются при исчислении коэффициентов связи.

Метод парных комбинационных группировок дает возмож­ность получить первоначальную информацию о взаимосвязи отдельных статистических показателей, проследить тенденцию изменения результативного признака в зависимости от фак­торного признака.

Использование количественного подхода и количествен­ных критериев в процессе социологического исследования про­блемы эффективности правовой нормы часто требует, получе­ния труднодоступной статистической информации. Надо дока­зать, что количественные изменения в объекте правового ре­гулирования произошли именно в результате действия этой правовой нормы, а не по каким-либо другим причинам. Со­бранные статистические данные целесообразно свести в сле­дующую таблицу (см. табл. 2).

Таблица 2. Таблица связи правовой нормы и регулируемых общественных отношении

 

Перед нами — известная схема математической статисти­ки. В математической статистике такие таблицы используют­ся для исследования взаимосвязи дихотомических признаков.*

* Латинская буква, взятая в скобки, означает число. Латинская буква, стоящая без скобок, означает наименование признака. Так, (А) — число, А — признак.

 

Первая строка таблицы (строка А) представляет случаи, когда действует новая правовая норма (новый вариант право­вой нормы).

Вторая строка таблицы (строка А) представляет случаи, когда новая правовая норма не действует, т. е. когда либо дей­ствовала старая правовая норма, либо данное общественное отношение вообще не было урегулировано правом.

Столбец В включает случаи, когда цель правового регу­лирования достигнута, а столбец — все остальные случаи.

Символы во внутренних клетках таблицы имеют значе­ния:

(АВ) — число наблюдаемых случаев достижения цели при условии действия новой нормы;

(А 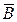) — число наблюдаемых случаев недостижения цели при условии действия новой нормы;

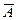( В) — число наблюдаемых случаев достижения цели при условии действия старой нормы;

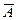
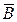( ) — число наблюдаемых случаев недостижения цели при условии действия старой нормы.

При отсутствии зависимости между А и B распределение альтернатив В и в подмножествах (А) и (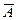) идентично, и наоборот, изменение распределений В в строках таблицы сви­детельствует о наличии зависимости между альтернативами А и В.

Количественным критерием позитивной связи между А и В является выполнение соотношений

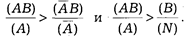
Аналогично для случаев отрицательной связи

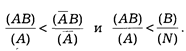
Таблица связи дихотомических признаков дает возмож­ность не только наглядно представить социологические дан­ные, но и сконструировать показатель эффективности — еди­нообразный метод сравнения эффективности одной и той же нормы в разных социальных условиях или же эффективности разных норм в одних и тех же условиях.

Наиболее приемлемым будет такой коэффициент, кото­рый равен 0, если новая норма не изменяет состояния регули­руемого объекта, и равен +1 при ее полной эффективности. Он будет иметь отрицательные значения, когда норма приво­дит к обратным по сравнению с намеченными результатам. Наконец, он. будет равен -1 в случаях, когда между действием нормы и состоянием регулируемого объекта имеется полная отрицательная связь.

Таким условием в наибольшей степени удовлетворяет ко­эффициент взаимосвязи дихотомических признаков, предло­женный известным английским статистиком Юлом:

Приведем условный пример расчета коэффициента Юла на практике. Пусть в нашу задачу входит измерение эффек­тивности применения к нарушителям дисциплины труда неко­торой санкции: например выговора. Индикатором достижения цели в данном случае может быть уровень повторных наруше­ний дисциплины труда, допущенных теми же лицами. В на­шем распоряжении имеются следующие данные (см. табл. 3).

Таблица 3. Эмпирические данные, характеризующие связь между действием санкции и совершением нового нарушения (пример)

Сначала проведем испытание наших данных на независи­мость. Критерием независимости двух признаков является вы­полнение соотношения

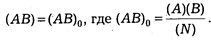
Испытание на независимость сводится к следующему. Сна­чала мы найдем величину (АВ)₀, затем (АВ). Если они не равны друг другу, то можно говорить о том, что исследуемые нами явления независимы. По данным таблицы 3 имеем:

Величина (АВ) ₀ показывает, по существу, какой должна быть численность лиц, повторно совершивших нарушения дис­циплины труда, если уровень рецидива не зависел бы от при­менения санкции.

В нашем примере величины (АВ) и (АВ) ₀ не равны.* Сле­довательно, гипотеза о независимости исследуемых призна­ков не подтверждается. Между действием санкции и вероят­ностью последующего правонарушения имеется статистичес­кая связь.

* Для подтверждения неслучайного характера, несовпадения (АВ) и (АВ)д следует прибегнуть к применению методов проверки статистических ги­потез.

 

Из соотношения

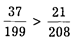
следует сделать вывод о том, что в данном случае связь меж­ду признаками А и В положительная.

Рассчитаем теперь точную меру эффективности данной санкции. Используем для этого формулу коэффициента Юла:

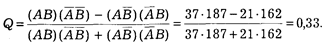
Мы видим, что положительная связь между действием санкции и числом повторных нарушений является довольно ощутимой.

Математическая статистика располагает обширным аппа­ратом измерения статистических связей. Так, в социально-пра­вовом исследовании довольно часто возникает задача измерения связей многозначных признаков, т. е. таких, каждый из которых имеет несколько значений (градаций). В математичес­кой статистике разработан комплекс методов измерения взаи­мосвязи многозначных признаков. Применяются следующие меры оценки взаимосвязи:

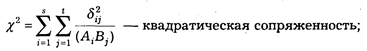
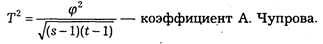
При составлении программного задания для ЭВМ некото­рые исследователи стремятся включить как можно большее число сопоставлений одних показателей с другими. К такой тенденции следует относиться с осторожностью.

При обработке социологической анкеты с та признаками число коэффициентов связи, которые могут быть вычислены, равно:

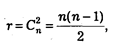
где — число сочетаний из n элементов по 2. Так, n = 10, r = 45; n = 20, r = 190 и т. д.

Отсюда видно, какой огромный запас производной инфор­мации скрыт даже в небольшой социологической анкете.

В ряде случаев исходные эмпирические данные имеют количественный характер, который допускает непосредствен­ное измерение какого-либо свойства у каждого из наблюдае­мых индивидов или объектов (возраст, образование, душевой доход, число совершенных в определенной местности и за оп­ределенный период преступлений и т. д.).

Показателем связи количественных признаков является коэффициент корреляции. Он вычисляется по формуле:

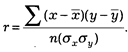
В этой формуле приняты следующие обозначения:

r — коэффициент корреляции;

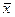— значение первого признака;

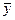— значение второго признака;

х — средняя величина из значений первого признака;

у — средняя величина из значений второго признака;

å — знак суммирования;

s _x — отклонение от средней величины первого признака;

s _y — отклонение от средней величины второго признака;

п — общее число наблюдений.

Корреляционный анализ дает ответ на вопрос, какова сте­пень тесноты связи. Используя коэффициент корреляции, мож­но определить роль каждого фактора в формировании резуль­тативного признака.

Вместе с тем, в процессе исследования взаимосвязей ко­личественных показателей можно поставить и другую задачу. Это задача определения формы связи двух переменных. Необ­ходимо решить вопрос: как, исходя из наблюдений над фак­торным признаком, определить соответствующее значение ре­зультативного признака? Это задача регрессионного анализа.

Уравнение регрессии устанавливает форму связи между факторным и результативным признаками. Эта связь может быть линейной или криволинейной. Если линия регрессии пря­мая, то говорят, что она линейна. Если линии регрессии име­ют ту или иную форму кривых линий, то говорят, что регрес­сия криволинейна.

Используя данную и подобные ей модели, можно дать, например, математическое описание взаимосвязи между рос­том численности населения определенного региона и динами­кой соответствующего числа преступных проявлений.

Для того чтобы составить уравнение регрессии, надо найти его коэффициенты. Для нахождения коэффициентов уравне­ния регрессии в математической статистике используется осо­бый метод, который называется методом наименьших квад­ратов. Он позволяет наилучшим образом подобрать к эмпири­ческим данным описывающую их линию (кривую, прямую).

Методы корреляционного анализа применялись для изу­чения связей между жесткостью судебной репрессии и состоя­нием судимости.* В целях количественного выражения жест­кости применялся особый коэффициент, который вычислялся по формуле

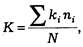
где k_i — коэффициент жесткости отдельных видов наказания; п_i — число осужденных к каждому виду наказания; N — об­щее число осужденных.

* Одной из ранних работ по применению корреляционного анализа в сфе­ре права было криминологическое исследование В. Н. Куфаева (1929 г.). На большом эмпирическом материале он вычислил коэффициенты кор­реляции между неурожаями и состоянием преступности в дореволюци­онной Самарской губернии. Эти коэффициенты оказались довольно вы­сокими.

 

В этом исследовании использовались статистические дан­ные четырех стран. СНГ за девять лет. Коэффициенты корре­ляции по каждой из взятых стран оказались следующими:

+0,07; -0,40; -0,63; -0,65.

Из приведенных данных вытекает; что в двух странах СНГ имеется четко выраженная обратная корреляционная связь между коэффициентами судимости и жесткостью судебной реп­рессии.

Методы корреляционного анализа использовались также для изучения статистической зависимости, которая существу­ет между сроком отбытого наказания и совершением нового преступления. В результате обработки эмпирических данных методами математической статистики было получено уравне­ние регрессии, характеризующее связь между числом лиц,. не совершивших нового преступления после отбытия наказа­ния, и сроком отбытого наказания. Это уравнение имеет сле­дующий вид:

у = 65,0 – 4,3 x,

где у — удельный вес лиц, не совершивших нового преступле­ния после отбытого наказания; х — срок отбытого наказания. В соответствии с данным уравнением увеличение срока отбытого наказания на один год приводит к повышению доли лиц, не совершивших нового преступления, на 4,3%. В целях измерения тесноты связи между указанными переменными было также рассчитано корреляционное отношение, которое в данном случае оказалось равным 0,9898. Другими словами, установлена такая связь, которая практически является фун­кциональной.

Сотрудники НИИ проблем укрепления законности и право­порядка Генеральной прокуратуры РФ В. И. Шинд и В. П. Рябцев выполнили большое статистическое исследование по определе­нию штатной численности прокурорских работников районного (городского) звена территориальных органов прокуратуры.

В результате расчетов на ЭВМ было получено уравнение регрессии.

Формула уравнения регрессии имеет следующий вид:

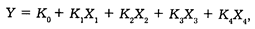
где Y — искомая штатная численность прокурорских работ­ников районного (городского) звена территориальных органов прокуратуры;

X ₁ — число зарегистрированных преступлений за год;

Х ₂ — численность населения (в тыс. чел.);

Х ₃ — число юридических лиц;

Х ₄ — размер территории (площадь в тыс. кв. км);

К ₀ — свободный член для расчета штатной численности прокурорских работников районного звена;

К ₁, К ₂, К ₃, К ₄ — коэффициенты при численном значении каждого фактора.

В результате применения ЭВМ были получены следую­щие коэффициенты уравнения регрессии:

К ₀ — 0,8 — величина' свободного члена;

К ₁ — 0,004710 — коэффициент при численном значении преступности;

К ₂ — 0,009550 — коэффициент при численном значении населения;

K ₃ — 0,00910 — коэффициент при численном значении юридических лиц;

К ₄ — 0,027120 — коэффициент при численном значении территории региона.

Зная официальные статистические данные (число райо­нов, преступность, численность населения, число юридичес­ких лиц — "поднадзорных объектов", площадь региона) и пе­ремножив эти факторы —аргументы на приведенные коэф­фициенты по указанной выше формуле, можно рассчитать потребную штатную численность прокуроров, их заместите­лей и помощников для любого региона Российской Федерации. Выполненная работа позволила сделать очень важные практи­ческие выводы.

§ 4. Создание и эксплуатация автоматизированных информационно-поисковых систем (АИПС) по статистике

Для эффективного использования данных правовой стати­стики в правотворческой деятельности принципиальное значе­ние имеет компьютеризация данной сферы. Федеральная целе­вая программа "Реформирование статистики в 1997—2000 гг." предусматривает в числе других мероприятий компьютериза­цию всех отраслей социальной статистики, включая правовую.*

* Утверждена постановлением Правительства

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: