Статья 4. Термины, используемые в настоящем Федеральном законе, и их определения

Государственная автоматизированная система Российской Федерации "Выборы" (ГАС "Выборы") — комплексы средств автоматизации, объединенные с использованием средств те­лекоммуникации в единую систему, предназначенную для со­вершенствования информационного обеспечения избиратель­ной системы Российской Федерации.

Комплекс средств автоматизации ГАС "Выборы" — сово­купность технических средств, программного и информацион­ного обеспечения, установленная в информационном центре (службе) избирательной комиссии.

Федеральный центр информатизации при Центральной избирательной комиссии Российской Федерации — государ­ственное учреждение, созданное для обеспечения функцио­нирования ГАС "Выборы".

Информационный центр ГАС "Выборы" субъекта Россий­ской Федерации — государственное учреждение или специа­лизированное структурное подразделение организации (уч­реждения, предприятия, общества), созданное для реализа­ции задач ГАС "Выборы" на уровне субъекта Российской Фе­дерации и действующее на постоянной основе.

Информационная служба территориальной (окружной) избирательной комиссии — подразделение в составе террито­риальной (окружной) избирательной комиссии, образуемое на время проведения выборов и референдумов для реализации задач ГАС "Выборы".

Системный администратор — должностное лицо, обеспе­чивающее функционирование комплекса средств автоматиза­ции, установленного в информационной службе территори­альной (окружной) избирательной комиссии.

Межвыборный период — период между проведением вы­боров и референдумов.

Приложение 2. Основные математические понятия и символы, примененные в Курсе

Множества

Множество — это совокупность элементов произвольной природы. Например, множество правовых норм, множество субъектов права, множество органов государства и т. д.

Понятие множества, взятое во всей его общности, лежит в основе всех разделов математики.

Символическое обозначение (конечного) множества:

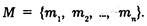
Множество А, составленное из некоторого числа элемен-. тов множества В, называется подмножеством множества А.

Объединение множества — математическая операция, заключающаяся в образовании из двух данных некоторого но­вого множества, каждый элемент которого принадлежит либо первому, либо второму множеству. Обозначение данной опе­рации:

Р = А È В.

Произведение (пересечение) множеств — математическая операция образования из двух данных множеств А и В некото­рого нового множества Q, каждый элемент которого принад­лежит множествам A и В одновременно. Обозначения данной операции:

Q= A Ç В.

Запись x Î X означает: элемент х принадлежит множе­ству X.

Запись Х Ì Y означает: множество Х является подмноже­ством некоторого множества Y.

Векторы и матрицы

Вектор — упорядоченный набор элементов некоторого множества.

Вектор обозначается так:

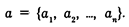
Например, вектором является набор признаков, взятых всегда в определенном числе и последовательности.

Каждый признак этого набора называется компонентой вектора.

Горизонтально расположенный вектор называется вектор-строкой.

Вертикально расположенный вектор называется вектор-столбцом.

Векторы с числовыми компонентами можно складывать или умножать на числа.

Любой вектор можно рассматривать как разновидность более сложного математического объекта — матрицы. Матри­цей называется прямоугольная таблица чисел, имеющая сле­дующий вид:

В этой матрице буквы а_ij означают какие-то числа или иные символы, а т и n всегда являются целыми числами: т обозначает число строк в данной матрице, а n — число столб­цов.

Как и векторы, матрицы можно складывать и умножать на число.

Функции

Как и понятие множества, понятие функции относится в математике к числу основных.

Функцией в математике называется некоторое правило F, согласно которому каждому элементу х данного множества А ставится в соответствие некоторый элемент y другого множе­ства В.

В символическом виде функция записывается так:

y = F(х),

где х Î А, у Î В.

Функцию можно описать словами или задать в форме математического выражения (например, у = 2 х ²).

Входящие в состав функции переменные х и у могут быть числами. В этом случае говорят о числовых функциях. Но эти же символы могут быть и объектами другой природы, т. е. выступать как качественные переменные. В таких случаях го­ворят о нечисловых функциях.

Числовые функции очень удобно изображать в форме некоторого графика (например, это может быть кривая ли­ния).

у = F (х ₁, х ₂ ,... х_p) — математическое обозначение функ­ции нескольких переменных.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: