 |
Математические модели схем ЭВС. Гиперграф
|
|
|
|
Для описания функционально-логических схем цифровых устройств и принципиальных электрических схем аналоговых устройств используются три основные математические модели (ММ): граф коммутационной схемы (ГКС); гиперграф (ГГ); взвешенный неориентированный граф (ВНГ).
Гиперграф
ГГ такое обобщение графа, в котором каждому ребру соответствует не пара вершин как в обычном графе, а произвольное подмножество вершин.
Данная модель обычно используется при решении задачи компоновки. Это связано с тем, что при компоновке контакты всегда распределяются в блок вместе с элементами, которым они инцидентны. Поэтому на ГКС можно исключить множество элементарных ребер W и F. При этом каждая цепь описываемая множеством контактов будет описываться множеством инцидентных ей элементов.
,
где E – множество элементов схемы;
U – множество ребер, при этом каждое ребро представляет собой подмножество элементов, инцидентных цепи vi. Для схемы примера (рис. 2.1) эти подмножества имеют вид:
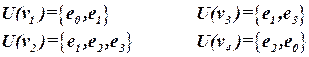
ГГ для схемы примера (рис. 2.1) представлен на рисунке 2.3.
Рис. 2.3
ГГ может быть описан с помощью матрицы инцидентности H.
Для схемы примера (рис. 2.1) матрица инцидентности имеет вид:
| v1 | v2 | v3 | v4 | |||
| e0 | ||||||
| H | = | e1 | ||||
| e2 | ||||||
| e3 |
Более удобно описывать ГГ с помощью списка цепей по элементам и списка элементов по цепям.
Список цепей по элементам представляется последовательностью чисел, определяющих номера цепей, причем подпоследовательность чисел, выделенная знаком “ ;” (точка с запятой), содержит номера цепей инцидентных одному элементу схемы.
Список элементов по цепям каждой подпоследовательностью чисел задает номера элементов, инцидентных некоторой цепи.
|
|
|
Вместо одного списка элементов по цепям с разделителями (“ ;”) можно использовать два списка SP и RSP вида:
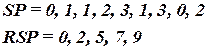
Аналогично для списка цепей по элементам:
При использовании пар списков SP–RSP или ST–RST в позициях начиная с RSP[i] (RST[i]) до RSP[i+1]-1 (RST[i+1]-1) в списке SP (ST) определяются номера элементов (цепей), инцидентных i –й(–му) цепи (элементу).
6.Алгоритм Прима построения КСД при ρ (xi)≤2.
Алгоритм Прима использует тот же принцип соединения ближайших вершин графа, что и алгоритм Краскала, но на каждом шаге к строящемуся дереву присоединяется ближайшая изолированная вершина.
В основе алгоритма Прима лежат 2 теоремы:
Tеорема 1. Каждая вершина минимального дерева непосредственно связана, по крайней мере, с одной ближайшей вершиной.
Теорема 2. Каждый изолированный фрагмент поддерева связан, по крайней мере, с одним из изолированных фрагментов кратчайшим ребром.
Локальная степень вершин 
- число ребер графа, инцидентных этой вершине.
Задача построения КСД с ограниченными локальными степенями возникает при проектировании проводных соединений, когда ограничено число паек к 1 контакту.
Предполагается, что задана матрица смежности C= 
n*n (матрица длин сегментов цепи); n-число контактов цепи.
Пусть необходимо построить КСД при 
(чаще всего m=2).
Для решения данной задачи можно применить алгоритм Прима с вычеркиванием строки, соответствующей вершине, локальная степень 
которой становиться равной «m».
Пример:
КСД без ограничений на 
:
L∑=14, локальная степень вершины x1 
.
Локальная степень вершин 
, L∑ ксд=17.
Алгоритм приближенный, результат зависит от выбора исходной вершины и от вершины, имеющей на текущем шаге равную минимальную оценку с другими, не включенными вершинами.
|
|
|
|
|
|
